Lab 6: Linked Lists II

A. Intro

Learning Goals

Today we're going to continue our discussion of linked lists. In particular, you will be introduced to the concept of encapsulation, doubly-linked lists, and sentinels.

To get started, download the code for Lab 6 using git.

Testing Your Code

We have provided a suite of JUnit tests for you in TestLab06.java. To run the tests, you can right click on TestLab06.java in IntelliJ and select Run 'TestLab06.java'. Afterward, you can select TestLab06 in the upper right corner of IntelliJ and press the green arrow to run the tests again.

Tip: It is a good practice to read the test code to be familiar with JUnit4, since you will soon be writing your own tests for future labs!

B. Encapsulation

The previous iteration of IntList that we learned is impractical to use at scale. In our current IntList, the notion of a node in the list and the list itself are not separate. This means that null checks would be scattered throughout code that uses the IntList, becoming increasingly difficult to maintain and understand. We want to separate the idea of the list as an entity from an entry in the list. This is called encapsulation, and we will see this used for every data structure we learn in the future.

Let's see what this looks like for our basic IntList. Note that in order to emphasize the encapsulation, break the normal box-and-pointer rule that we don't put Objects inside other Objects. You do not have to do so, but it does help with the visual.

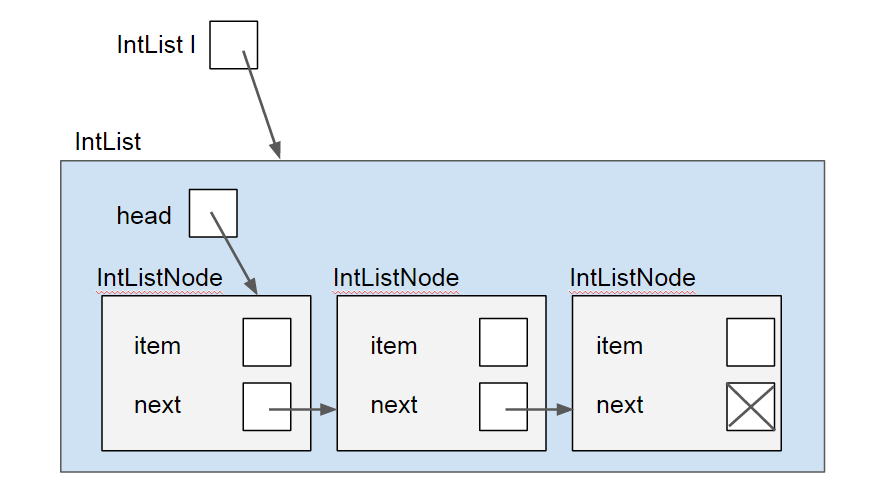
intlist

In code, it looks like this:

public class IntList {

    /**
     * The head of the list is the first node in the list.
     * If the list is empty, head is null
     */
    private IntListNode head;
    private int size;

    /**
     * IntListNode is a nested class. It can be instantiated
     * when associated with an instance of IntList.
     */
    public class IntListNode {
        int item;
        IntListNode next;

        public IntListNode(int item, IntListNode next) {
            this.item = item;
            this.next = next;
        }
    }

    ... more methods to operate on ...
}

All operations on the list are handled through an instance of an IntList object. In turn, the IntList object operates directly on the IntListNodes that make up the IntList. Note that IntListNode does not need any methods (other than some utility toString(), equals(), and other methods, which you will add later). The main effect of this is that code that wants to interact with the IntList needs to know nothing about the internal representation of the list or how the operations will take place. Instead, the code simply tells the list what it needs and the IntList representation itself will take care of the operations, including any null checks, size checks, or further operations.

Exercise: toString() and equals()

Normally, we would ask you to manually write out these methods to convert a list into its String representation and to write an equality checker. However, since we're using IntelliJ, let's utilize one of its features - automatic code generation.

Move your blinking cursor to somewhere inside the IntListNode class and press Alt+Insert (or on Mac, Command+N). This should bring up a "Generate" menu where your cursor is - go ahead and select "toString()", take a look at the dialog, and press OK. You'll notice a toString() method is generated for the IntListNode class, using the fields you specified (both fields should have been highlighted). Now pull up the menu again, and this time select "equals() and hashCode()". Look at the dialog boxes, press OK & next as needed, and you'll see the equals() and hashCode() methods appear automatically. You can feel free to delete the hashCode() method as we won't need it and will be learning about it later in the course.

Repeat the process with your cursor inside the IntList class, and now you'll have equals() and toString() methods automatically generated and working. This doesn't work 100% of the time (as we'll see later on), but it's a great way to get a framework going quickly. You can even generate constructors, getters and setters, and so on!

Exercise: Implement insert()

As a bit of practice working with such lists, fill in the insert() method in IntList.java. Note that this is not the same IntList as used in the previous lab. While it seems obvious, it may be helpful to think that, for example, inserting into position 1 is equivalent to finding the node at position 0 and inserting after it.

Exercise: Implement merge()

Suppose two high schools in a school district both have running teams. Each maintains a sorted IntList storing their athletes' 800 meter times to the nearest second. Now suppose the two high schools want to make a combined school district team. How would they choose the fastest runners from both schools?

This is just one real-world use for the merge() function, an interesting utility that you may have touched upon in CS 61A.

Implement the non-destructive static method merge() in your IntList class. This method will take as input two sorted IntLists and return the IntList that contains all elements from both input IntLists in sorted order.

(Optional) Exercise: Implement remove()

Fill in the remove() method in IntList.java. Make sure to take care of edge cases, like removing the last element in the list.

C. Reverse

Over the next few steps, we're going to be working on a method to reverse an IntList using our current IntList implementation.

Reversing a List in Place

To reverse the list in place, we recommend using a static helper method.

Here's the framework code for reverse(). Don't fill it in yet.

public void reverse() {
    // ...
}

public static IntListNode reverseHelper(IntListNode l, IntListNode soFar) {
    // ...
}

An Invariant for Reversing a List

This framework suggests we maintain a recursion invariant (something that must always be true) that relates the values of l and soFar at each call.

Here is a trace of a call to reverse with the list {A, B, C, D}:

Method called l soFar
reverse (A, B, C, D) N/A
reverseHelper (A, B, C, D) ( )
reverseHelper (B, C, D) (A)
reverseHelper (C, D) (B, A)
reverseHelper (D) (C, B, A)
reverseHelper ( ) (D, C, B, A)

Exercise: Completing the reverse() Method

Whenever reverseHelper() is called, l is the list of elements not yet reversed, and soFar is the reversed list of the elements already processed. To design the procedure from this relationship, we position ourselves in the middle of the recursion, say, with l equal to (C D) and soFar equal to (B A). What do we do with C, the next element in l, so that soFar is the reverse of (A B C)? The answer is to add it to the current soFar.

Here's reverseHelper()'s header:

private static IntListNode reverseHelper(IntListNode l, IntListNode soFar) {
    if (l == null) {
        return soFar;
    } else {
        ...
    }
}

Again, we position ourselves in the middle of the recursion. For design in Java, it helps to draw box-and-pointer diagrams; here's the situation with l pointing to the list (C D) and soFar pointing to the list (A B).

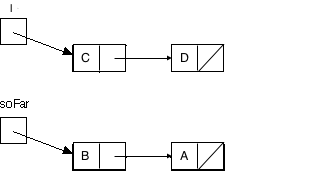
reverse1

By the next recursive call, we want our lists to look as follows:

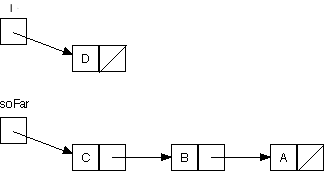
reverse2

There are three changes to be made. All are interdependent, though, so we'll need a temporary variable:

IntListNode temp = l.next;
l.next = soFar;
return reverseHelper( ____ , ____ );

Copying the correct arguments in the recursive call will provide the other two changes.

Fill in the arguments of the recursive call to complete reverseHelper(). Then, fill in reverse().

D. The Standard Doubly-linked List

There are some major issues, both efficiency-wise and code-simplicity-wise with the linked list implementations we've been working with so far:

  1. It's easy to insert into the front of the list, but requires a lot more work to insert into the back of the list.
  2. If we want to remove a node in our linked list, even if we have a reference to the node we want to remove, we have to traverse until we find the node before it in order to remove it.
  3. Due to an empty list being represented by the head field being null, and the end of a list being represented by the next field being null, there are null checks and special cases everywhere in the code.

The solution to the first two problems is to use a doubly-linked list. Each node keeps track of the node after and before itself. Instead of just a head pointer, the list object maintains both a head and tail pointer, to the front and back of the list respectively. It looks like this:

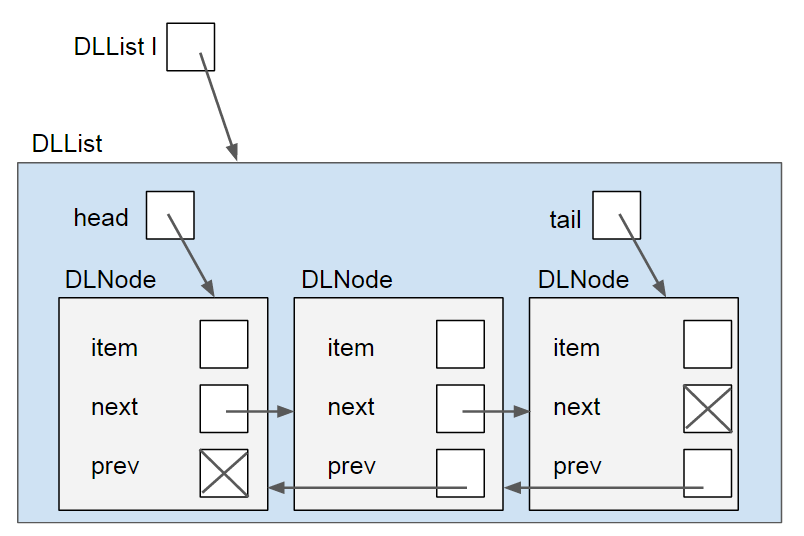
encapsulation

This adds a bit of complexity to the operations, but allows for constant time insertion to the front and back, and allows the user to traverse the list either forwards or backwards. Additionally, this allows the list to delete any nodes, even in the middle of the list, in constant time without traversing to the middle as long as it has a reference to the node that needs to be deleted.

This doesn't fix the issue of many null checks. However, in conjunction with the doubly-linked list, we can eliminate null checks and simplify the code greatly with usage of a sentinel node instead of head and tail pointers. The sentinel node always exists, and does not represent an actual node in the list. Its next field represents the front of the list and it's prev field represents the back of the list. The sentinel's item is null, and an empty list is represented by just a sentinel node pointing to itself. In a box-and-pointer diagram, it looks like this:

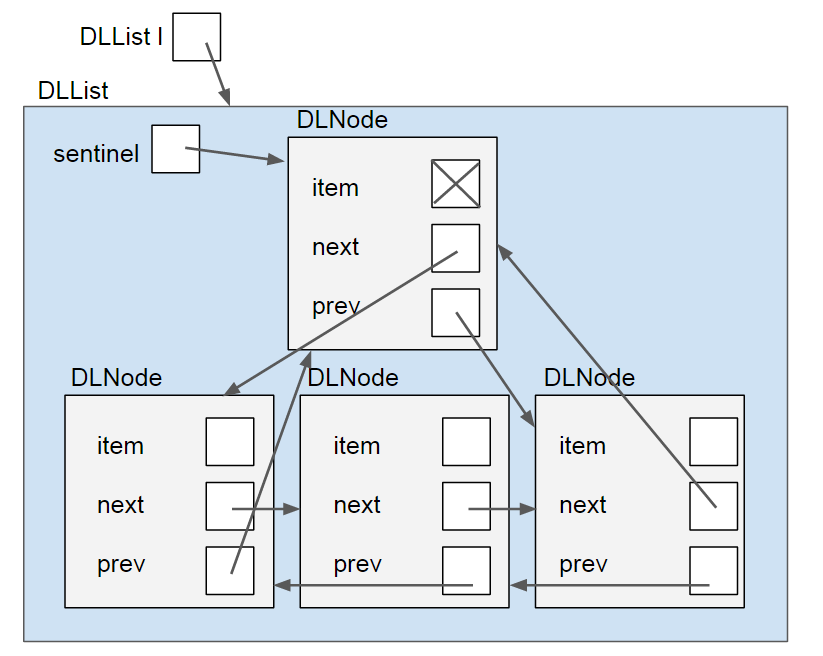
sentinel

This has many benefits. When iterating through the list, we do not need to worry about reaching a null pointer at any point; when our moving pointer reaches the sentinel, it's the end of the list. When inserting and removing nodes, we don't need to manually handle being near the end or beginning or being the first or last element inserted or removed of the list; the code can be written with disregard for edge cases and it will still work properly because of the sentinel. Because of this, the doubly-linked list with a sentinel node is typically used in practice as the linked list representation, like in Java's own standard library class, java.util.LinkedList.

Finally, note one last thing - in the diagrams above, it's clear that sentinel, next and prev point to DLNode objects. However, item is ambiguous and doesn't point to anything. This is because in our new list, item will be an Object, which can hold any type. Instead of using only ints like before, we allow our list to be more robust, like python lists, holding mixtures of any kind of object. In a later lab, we will further improve on our design with generics, but for now you can add items to your DLList and print out their values without fear of type problems, like so:

public static void main(String[] args) {
    DLList l = new DLList();
    l.insertBack("CS"); //String
    l.insertBack(61); //Integer
    l.insertBack("BL!");
    System.out.println("l = " + l);
}

$ java DLList
l = DLList(CS, 61, BL!)

Note that if we want to actually manipulate anything out of our list, we'd have to cast it, like so:

Integer sixtyone = (Integer) l.get(1);

Although you won't be needing to do any of that.

Exercise: Implement insert(), insertFront(), and both remove() methods

Fill in insert(), insertFront(), and both remove() methods in DLList.java. Read through the existing code - some of it can be used as a reference and example for how you can structure your methods. You should never need to type the word null or do any edge case checking. Your only if statement should be in remove(Object o).

E. Double In Place and Reverse, revisited

Exercise: Implement doubleInPlace()

Implement the method doubleInPlace(). Each node in the list should be copied in place, resulting in a list that's twice as long. For example, if the list initially contains (a, b, c), it should contain (a, a, b, b, c, c) after the call to doubleInPlace(). Is this a destructive or non-destructive method?

Don't call any methods other than the DLNode constructor, and don't call it more than once per node in the original list. Draw a box-and-pointer diagram if you're stuck!

Exercise: Implement reverse()

Implement reverse() iteratively in DLList.java. As before, we do not need any null checks or special cases. You should be able to do this only iterating through the list once and flipping all the pointers around as you go - try drawing a box-and-pointer diagram before you start.

F. Conclusion

Summary

You should have some more practice with working with linked lists and their various representations - singly vs doubly-linked with sentinel. We also saw some different ways to implement things - recursively and iteratively, both with their tradeoffs.

Deliverables

Here's a short summary on what you need to do to complete this lab: