A. Intro
Pull the files for lab 12 from the skeleton repository with git pull skeleton master and make a new IntelliJ project out of them.
In earlier labs, we were discussing and implementing different variants of Linked Lists. In this lab and the next few, we will talk about a data structure called a tree. The meaning of the tree data structure originates from the notion of a tree in real life.
Below is a conceptual visualization of a tree. It's not really a box and pointer diagram and should not be interpreted as a literal implementation in Java.
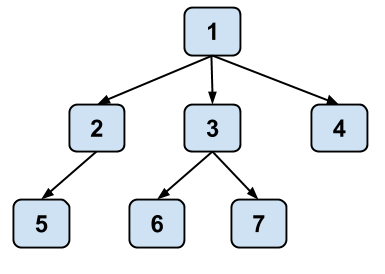
Note that while a tree in real life is rooted at the bottom and branches out upwards, trees in computer science are typically drawn such that they are rooted at the top and branch out downwards.
Some Vocabulary
In order to be able to talk about trees, we first need to define some terminology.
| Term | Description | Example Above |
|---|---|---|
| Node | Single element in a tree | 1, 2, 3, 4, 5, 6, and 7 are all nodes. |
| Edge | A connection between two nodes | There is a direct edge from 1 to 2, but there is no direct edge from 1 to 7. |
| Path | A series of one or more edges that connects two nodes | There is a path from 1 to 7, consisting of edges 1↔3 and 3↔7. |
| Leaf | A node with no children | 4, 5, 6, and 7 are leaf nodes. |
| Root | The topmost node, which does not have a parent | 1 is the root node. |
Relationships
These following terms are defined with respect to a particular node.
| Term | Description |
|---|---|
| Child | Directly below the current node |
| Parent | Single node connected directly above the current node |
| Siblings | Nodes with the same parent |
| Ancestors | All nodes on the path from the selected node up to and including the root |
| Descendant | All the children, children's children, and so forth of a node |
| Subtree | The tree consisting of the node and all of its descendants |
| Height | The length of the path from the node to its deepest descendant. By length, we mean the number of edges traveled along a given path. Therefore, the height of a leaf node is 0. (Note: There is an alternate definition of height as the number of nodes traversed. In that case, the height of a leaf would be 1.) |
| Depth | The length of the path from the node to the root. The depth of the root node is 0 |
We can also define the height of a tree and the depth of a tree, and it is usually assumed that this refers to the height of the root node and the depth of the deepest leaves respectively.
Definition
For a linked structure to be considered a tree, no node can have multiple parents. Further, there can be no cycles (paths that start and end at the same node). There can only be one path between any two nodes in a tree. Finally, all nodes must be a descendent of the root (except the root itself).
Discussion: Examples of Trees
Discuss with your partner whether the following examples would be considered trees as we've introduced them.
- Linked List
- Family Tree
- Amoeba Family Tree (single entities - amoebas - create any number of children)
B. Amoeba Family Tree
An amoeba family tree is an example of our above definition of a tree. It is simpler than a normal family tree because amoebas do not need partners in order to reproduce. An amoeba has one parent, zero or more siblings, and zero or more children. An amoeba also has a name.
Below is the skeleton code for an Amoeba. The full code is located at lab12/AmoebaFamily.java.
class Amoeba {
String name;
Amoeba parent;
ArrayList<Amoeba> children;
}And below is a box and pointer diagram.
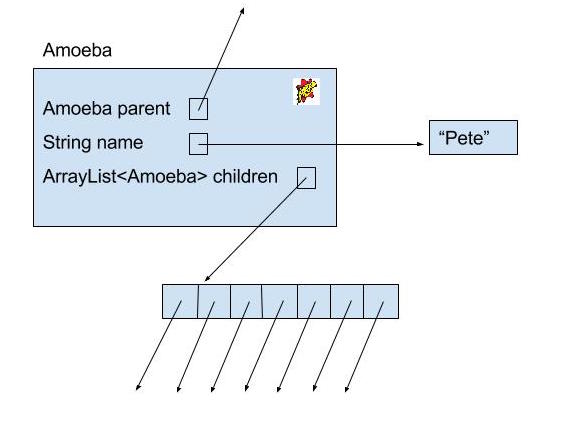
Amoebas (or amoebae) live dull lives. All they do is reproduce. So all we need to keep track of them are the following methods:
/**
* A constructor that starts an Amoeba family with an amoeba
*/
public AmoebaFamily(String name) {
root = new Amoeba(name, null);
}
/**
* Adds a new Amoeba with childName to this AmoebaFamily
* as the youngest child of the amoeba named parentName
* Precondition: This AmoebaFamily must contain an Amoeba named parentName.
*/
public void addChild(String parentName, String childName) {
if (root != null) {
root.addChild(parentName, childName);
}
}
/**
* Print the amoeba family tree.
*/
public void print() { ... }Void Recursive Methods
In the AmoebaFamily class we provided the method addChild to add a new Amoeba to the AmoebaFamily tree. The method implements a general traversal of the tree using a void recursive method. You are going to write three other traversals that use a void recursive method. Your goal is to make the solution to the three methods as similar as possible to addChild.
Exercise: Make All Names Lowercase
/**
* Changes the names for all Amoebas in this AmoebaFamily to use only
* lowercase letters.
*/
public void makeNamesLowercase() {
// Your goal is to make this as similar as possible to addChild
}Exercise: Replace the Name of an Amoeba
/**
* Replaces the name of an amoeba named currentName with the name newName.
* Precondition: This AmoebaFamily contains exactly one Amoeba named currentName.
*/
public void replaceName(String currentName, String newName) {
// Your goal is to make this as similar as possible to addChild
}Exercise: Print the Names of All Amoebas in the Family.
/**
* Print the names of all amoebas in the family, one on each line.
* later you will write print() that has more interesting formatting
*/
public void printFlat() {
// Your goal is to make this as similar as possible to addChild
}Exercise: Pretty Print
You're going to write a more interesting print method. It should print the root amoeba's name and the names of all its descendants. One name should be printed per line. The names of the children of each descendant Amoeba should be printed on the lines immediately following. Each name should be indented four spaces more than the name of their parent Amoeba. Thus the output should appear in the form
amoeba_name
child_name
grandchild_name
great_grandchild_name
great_great_grandchild_name
grandchild_name
child_name
grandchild_name
child_name
child_name
grandchild_nameYou will probably need a helper method whose argument keeps track of the indenting level, but the form should still be similar to addChild and the other three examples you worked with.
Non-void Recursive Methods
All of the methods we have written for the AmoebaFamily class have not returned anything! All they have been doing is modifying the state of the AmoebaFamily. We will be able to do cooler things if we can return values. The next example will take advantage of this.
Longest Name
First, switch which partner is coding for this lab, if you haven't already.
We've provided the following method:
/**
* Finds the length of the longest name between this Amoeba and
* its children
* @return the length of the longest name
*/
public int longestNameLength() {
int maxLengthSeen = name.length();
for (Amoeba a : children) {
maxLengthSeen = Math.max(maxLengthSeen, a.longestNameLength());
}
return maxLengthSeen;
}Your goal is to write a method longestName that is as similar to longestNameLength as possible. The goal is to try to identify the pattern in these non-void recursive methods. You will use the patterns here in the next two exercises.
/**
* Returns the length of the longest name in this AmoebaFamily
* @return The length of the longest name in this AmoebaFamily
*/
public int longestNameLength() {
if (root != null) {
return root.longestNameLength();
}
return 0;
}Amoeba Counting
Write and test an AmoebaFamily method named size that returns the number of amoebas in this AmoebaFamily.
OPTIONAL: Finding the Busiest Amoeba
Consider an AmoebaFamily method named busiest, which returns the name of the amoeba with the most children.
If there are more than one amoeba with the same maximum number of children, you may return the name of any of them. If the tree is empty, return null.
Hint: The longestName method is a good model for busiest. Depending on your implementation, you may find that you need to keep track of two sets of information, but your helper method can only return one thing. Think flexibly and consider what you can return that will help keep track of those two sets of information.
Computing the Height
The height of a node in a tree is the maximum length of a downward path from that node to a leaf. For now, we'll define the height of a leaf as 0, and the height of a null tree as -1. Sometimes you'll see a different convention, defining the height of a leaf as 1, and the height of a null tree as 0.
The following code is an incorrect implementation of the height method. Discuss with your partner what the bug is.
//In Amoeba
private int height() {
if (children.isEmpty()) {
return 0;
} else {
int bestSoFar = 0;
for (Amoeba a : children) {
bestSoFar = 1 + Math.max(a.height(), bestSoFar);
}
return bestSoFar;
}
}Then write a JUnit test that includes the case you identified and one other case. Then fix the implementation of the height method. This means include a height method in the AmoebaFamily class, similarly to all the other AmoebaFamily methods you've written so far.
C. Binary Trees
As noted earlier, a common special case is a binary tree, one in which each node has at most two children. Rather than store the children in an ArrayList as was done in Amoeba nodes, one normally just has two separate variables left and right for the left and right children.
Three processing sequences for nodes in a binary tree occur commonly enough to have names:
- preorder: process the root, process the left subtree (in preorder), process the right subtree (in preorder)
- postorder: process the left subtree (in postorder), process the right subtree (in postorder), process the root
- inorder: process the left subtree (in inorder), process the root, process the right subtree (in inorder)
Exercises with Processing Sequences
With your partner, determine the preorder, inorder, and postorder processing sequence for the tree below. Then, verify your answers below.
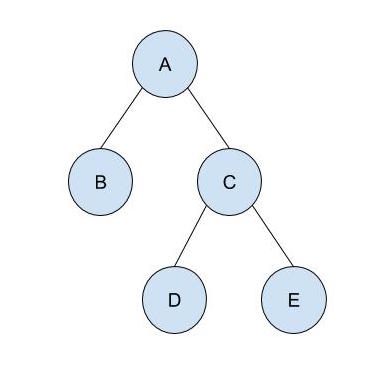
preorder:
A B C D E
inorder:
B A D C E
postorder:
B D E C A
A BinaryTree Class
The file lab12/BinaryTree.java defines a BinaryTree class and a TreeNode class. First, read the code, and predict what output will be produced by the statement
print(t, "sample tree 2");in the main method. Run the program to verify your answer.
Then provide a fillSampleTree3 method that initializes the BinaryTree version of the tree pictured below.
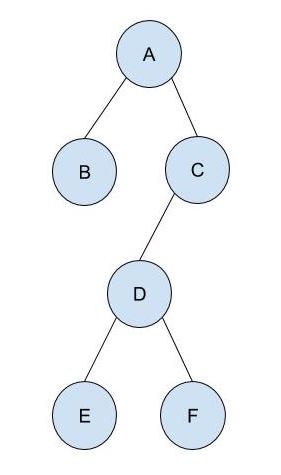
Run the program to verify your answer.
Height Method
First, switch which partner is coding if you haven't recently.
Add a height method to the BinaryTree class, similar to the AmoebaFamily height method you worked with earlier. The height of an empty tree is 0; the height of a one-node tree is 1; the height of any other tree is 1 + the greater of the heights of the two children. Test your method on the various sample trees.
Is Completely Balanced
Then provide an isCompletelyBalanced method for the BinaryTree class. An empty tree and a tree containing just one node are both completely balanced; any other tree is completely balanced if and only if the height of its left child is equal to the height of its right child, and its left and right children are also completely balanced. Test your method on the various sample trees, as well as a completely balanced tree of height 3.
D. Loose Ends
We will finish this lab with some loose ends that will prepare us for traversals, which we will study in the next lab.
Stacks and Queues
The first data structure was the LinkedList data structure. That data structure allowed for adding and removing at any position. However sometimes that is too powerful and we do not need all of that functionality. Thus, we will introduce the stack and the queue data structures, which are like lists, but have more limited, precise functionality. As you go through this section, think about how you can implement stacks and queues by using a LinkedList.
Stack
A stack data structure models a stack of papers, or plates in a restaurant, or boxes in a garage or closet. A new item is placed on the top of the stack, and only the top item on the stack can be accessed at any particular time. Stack operations include the following:
- pushing an item onto the stack;
- accessing the top item of the stack;
- popping the top item off the stack;
- checking if the stack is empty.

Queue
A queue is a waiting line. As with stacks, access to a queue's elements is restricted. Queue operations include:
- adding an item to the back of the queue;
- accessing the item at the front of the queue;
- removing the front item;
- checking if the queue is empty.

E. Working with Stacks and Queues
Exercise 1
Suppose that the following sequence of operations is executed using an initially empty stack. What ends up in the stack?
push A
push B
pop
push C
push D
pop
push E
popAC
Exercise 2
Suppose that the following sequence of operations is executed using an initially empty queue. What ends up in the queue?
add A
add B
remove
add C
add D
remove
add E
removeDE
F. Conclusion
Deliverables
To finish this lab, make sure to finish the following:
- Read through the lab and understand how
AmoebaFamilyand Binary trees work. Make sure to also read through the loose-ends involving stacks and queues. - Write a JUnit test identifying what was wrong with the given method for calculating an amoeba's
height(). Make sure you have completed the following methods in
AmoebaFamily:- public void makeNamesLowercase();
- public void replaceName(String currentName, String newName);
- public void printFlat();
- public void print();
- public String longestName();
- public int size();
- public int height();
And finally complete the following methods in
BinaryTree:- public void fillSampleTree3();
- public int height();
- public boolean isCompletelyBalanced();