A. Intro
There will be no skeleton files and you will continue to use the files from the previous lab. Please copy the files from lab12 into the lab13 directory in your repository. This lab covers the tools and techniques related to traversing the nodes of a tree structure.
B. Building a Tree Iterator
We now consider the problem of returning the elements of a tree one by one, using an iterator. To do this, we will implement the interface java.util.Iterator. The first technique to traverse trees that we will examine is depth-first iteration or depth-first search. The general idea is that we walk along each branch, traveling as far down each branch as possible before turning back and examining the next one. We will see that this is actually quite straightforward to implement.
We will also use a nested iteration class to hide the details of the iteration from the outer class. As with previous iterators, we need to maintain state-saving information that lets us find the next tree element to return, and we now must determine what that information might include. To help work this out, we'll consider the sample tree below, with elements to be returned depth first as indicated by the numbers.
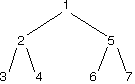
The first element to be returned is the one labeled "1". Once that's done, we have a choice whether to return "2" or "5".
Suppose we break ties by lowest node label. As a result, based on our tie-breaking rule, we will pick "2" over "5". Once we return element "2", we have a choice between return "3" or "4" next. But don't forget about "5" from earlier!
Next, we return "3", again based on our tie-breaking rule. At this point, we still remember that we need to return to "4" and "5" as in the diagram below.

That means that our state-saving information must include not just a single pointer of what to return next, but a whole collection of "bookmarks" to nodes we've passed along the way.
More generally, we will maintain a collection that we'll call the fringe or frontier, containing all the nodes in the tree that are candidates for returning next. The next method will choose one of the elements of the fringe as the one to return, then add the returned element's children to the fringe as candidates for the next element to return. hasNext returns true when the fringe isn't empty.
The iteration sequence will then depend on the order we take nodes out of the fringe. Depth-first iteration, for example, results from storing the fringe elements in a stack, a last-in first-out structure. The java.util class library conveniently contains a Stack class with push and pop methods. We illustrate this process on a binary tree in which TreeNodes have 0, 1, or 2 children named left and right. Here is the code:
public class DepthFirstIterator implements Iterator<TreeNode> {
// Where we will store our bookmarks
private Stack<TreeNode> fringe = new Stack<TreeNode>();
public DepthFirstIterator(TreeNode root) {
if (root != null) {
fringe.push(root);
}
}
// Returns whether or not we have any more "bookmarks" to visit
public boolean hasNext() {
return !fringe.isEmpty();
}
/** Throws an exception if we have no more nodes to visit in our traversal. Otherwise,
it picks the most recent entry to our stack and "explores" it. Exploring it requires
visiting the node and adding its children to the fringe, since we must eventually
visit them too.
*/
public TreeNode next() {
if (!hasNext()) {
throw new NoSuchElementException("tree ran out of elements");
}
TreeNode node = fringe.pop();
if (node.right != null) {
fringe.push(node.right);
}
if (node.left != null) {
fringe.push(node.left);
}
return node;
}
// We've decided not to use it for this example
public void remove(){
throw new UnsupportedOperationException();
}
}Stack Contents during Depth-First Iteration
For the following exercises, assume that we push the right child before the left child of a node onto the fringe.
Exercise 1
What numbers are on the stack when element 4 in the tree below has just been returned by next? (The top of the stack is to the left and the bottom of the stack is to the right)
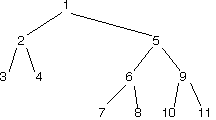
5
Exercise 2
For the same image above, what numbers are on the stack when element 6 in the tree below has just been returned by next? (The top of the stack is to the left and the bottom of the stack is to the right)
7, 8, 9
Effect of Pushing Left Child Before Right
Suppose the next code pushes the left child onto the stack before the right:
if (node.left != null) {
fringe.push(node.left);
}
if (node.right != null) {
fringe.push(node.right);
}In what order are the elements of the tree above returned? Discuss with your partner, then check your answer below.
Answer: 1 5 9 11 10 6 8 7 2 4 3
A Depth-First Amoeba Iterator
Complete the definition of the AmoebaIterator class (within the AmoebaFamily class). It should successively return names of Amoebas from the family in preorder. You will need to add Amoebas to the stack as you do above, with the right child being pushed before the left child. Thus, for the family set up in the AmoebaFamily main method, the name "Amos McCoy" should be returned by the first call to next; the second call to next should return the name "mom/dad"; and so on. Do not change any of the framework code.
Organizing your code as described in the previous step will result in a process that takes time proportional to the number of Amoebas in the tree to return them all. Moreover, the constructor and hasNext both run in constant time, while next runs in time proportional to the number of children of the element being returned.
Add some code at the end of the AmoebaFamily main method to test your solution. It should print names in the same order as the call to family.print(), though without indenting.
A Breadth-First Amoeba Iterator
Now rewrite the AmoebaIterator class to use a queue (first-in, first-out) instead of a stack. (You might want to save your previous code for future reference, though you will be including this version in your submission.) This will result in amoeba names being returned in breadth-first order. That is, the name of the root of the family will be returned first, then the names of its children (oldest first), then the names of all their children, and so on. For the family constructed in the AmoebaFamily main method, your modification will result in the following iteration sequence:
Amos McCoy
mom/dad
auntie
me
Fred
Wilma
Mike
Homer
Marge
Bart
Lisa
Bill
HilaryYou may use either a list (your own List or the builtin LinkedList) to simulate a queue, or any subclass of the builtin java.util.Queue interface.
The idea behind breadth-first search is to explore each level of the tree before exploring the next. Try working out this traversal on paper with the prior exercises to gain intuition for it.
C. Build and Check a Tree
Printing a Tree
We now return to binary trees, in which each node has either 0, 1, or 2 children. Last lab, we worked with an implementation of binary trees using a BinaryTree class with a nested TreeNode class, as shown below.
public class BinaryTree {
private TreeNode root;
public static class TreeNode {
public Object item;
public TreeNode left;
public TreeNode right;
public TreeNode (Object obj) {
item = obj;
left = right = null;
}
public TreeNode (Object obj, TreeNode left, TreeNode right) {
item = obj;
this.left = left;
this.right = right;
}
...
}
...
}The framework is available in BinaryTree.java.
Copy the following code into BinaryTree.java and fill in the blanks in the following code to print a tree to see its structure as described below.
//Copy into BinaryTree class
public void print() {
if (root != null) {
root.print(0);
}
}
//Copy into TreeNode class
private static final String indent1 = " ";
private void print(int indent) {
// TODO your code here
println (item, indent);
// TODO your code here
}
private static void println(Object obj, int indent) {
for (int k=0; k<indent; k++) {
System.out.print(indent1);
}
System.out.println(obj);
}The print method should print the tree in such a way that if you turned the printed output 90 degrees clockwise, you see the tree. Here's an example:
Tree
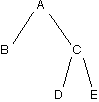
Printed Version
E
C
D
A
BTest your method by adding some code to the main method of BinaryTree and checking your trees with the sample trees!
Checking a BinaryTree object for validity
First, switch which partner is coding this lab if you haven't already.
A legal binary tree has the property that, when the tree is traversed, no particular node appears more than once in the traversal. A careful programmer might include a check method to check that property:
public boolean check() {
alreadySeen = new ArrayList();
try {
isOK(root);
return true;
} catch (IllegalStateException e) {
return false;
}
}
// Contains nodes already seen in the traversal.
private ArrayList alreadySeen;
(IllegalStateException is provided in Java.)Add the check method to BinaryTree.java. In the same file, write and test the isOK method, using variations of the sample trees you constructed for earlier exercises as test trees. Here's the header:
private void isOK(TreeNode t) throws IllegalStateException;You may use any traversal method you like. You should pattern your code on earlier tree methods you have written.
Incidentally, this exercise illustrates a handy use of exceptions to return from deep in recursion.
Analyzing isOK's running time
Complete the following sentence.
The isOK method, in the worst case, runs in time proportional to ______ , where N is ________________ .
Briefly explain your answer to your partner.
N^2, number of nodes in the tree. (contains for an ArrayList will take linear time with respect to the number of elements in the list.)
N is also acceptable if you use a Set instead of an ArrayList.
Building a Fibonacci Tree
This exercise deals with "Fibonacci trees", trees that represents the recursive call structure of the Fibonacci computation. (The Fibonacci sequence is defined as follows: F0 = 0, F1 = 1, and each subsequent number in the sequence is the sum of the previous two.) Let n be the argument passed in to the fibTree method. The root of a Fibonacci tree should contain the value of the nth Fibonacci number, the left subtree should be the tree representing the computation of the n-1th Fibonacci number, and the right subtree should be the tree representing the computation of the n-2th Fibonacci number. The two exceptions to this rule are when we pass in 0 or 1 to the fibTree method. The first few Fibonacci trees appear below.
| Function | Graph |
|---|---|
fibtree(0) |
 |
fibtree(1) |
 |
fibtree(2) |
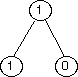 |
fibtree(3) |
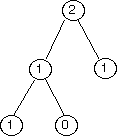 |
fibtree(4) |
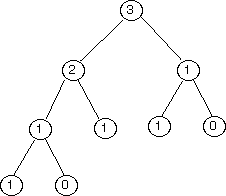 |
fibtree(5) |
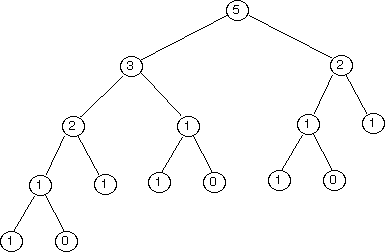 |
Supply the static fibTree method in BinaryTree that takes in a nonnegative integer n, and returns a Binary Tree that stores the n-th Fibonacci value using the representation above.
public static BinaryTree fibTree(int n) {
BinaryTree result = new BinaryTree();
}Building an Expression Tree
Compilers and interpreters convert string representations of structured data into tree data structures. For instance, they would contain a method that, given a String representation of an expression, returns a tree representing that expression. Note: Make sure that all of the items in this tree are Strings (not chars or Integers).
Copy the following code into your BinaryTree class. Complete (fill in the blanks) and test the following helper method for exprTree.
public static BinaryTree exprTree(String s) {
BinaryTree result = new BinaryTree();
result.root = result.exprTreeHelper(s);
return result;
}
// Return the tree corresponding to the given arithmetic expression.
// The expression is legal, fully parenthesized, contains no blanks,
// and involves only the operations + and *.
private TreeNode exprTreeHelper(String expr) {
if (expr.charAt(0) != '(') {
____; // you fill this in
} else {
// expr is a parenthesized expression.
// Strip off the beginning and ending parentheses,
// find the main operator (an occurrence of + or * not nested
// in parentheses, and construct the two subtrees.
int nesting = 0;
int opPos = 0;
for (int k = 1; k < expr.length() - 1; k++) {
// you supply the missing code
}
String opnd1 = expr.substring(1, opPos);
String opnd2 = expr.substring(opPos + 1, expr.length() - 1);
String op = expr.substring(opPos, opPos + 1);
System.out.println("expression = " + expr);
System.out.println("operand 1 = " + opnd1);
System.out.println("operator = " + op);
System.out.println("operand 2 = " + opnd2);
System.out.println();
____; // you fill this in
}
}Given the expression ((a+(5*(a+b)))+(6*5)), your method should produce a tree that, when printed using the print method you wrote earlier, would look like
5
*
6
+
b
+
a
*
5
+
aOptimizing an Expression Tree
Again, switch which partner is coding for this lab if you haven't recently.
Given a tree returned by the exprTree method, write and test a method named optimize that replaces all occurrences of an expression involving only integers with the computed value. Here's the header.
public void optimize()optimize will call a helper method as other BinaryTree methods did in earlier exercises.
For example, given the tree produced for
((a+(5*(9+1)))+(6*5))your optimize method should produce the tree corresponding to the expression
((a+50)+30)Don't create any new TreeNodes; merely modify those already in the tree. Remember all items of the TreeNodes should be Strings (even the numbers!). A helper method to check if a String is an Integer may be useful. Here's the header.
public boolean validateInt(String s)You may see a lot of casting in this method because TreeNode's item field is an Object. This is why, in most other cases, we use generics!
D. Conclusion
Readings
The next lab will cover binary search trees. If you are interested in reading a bit about them beforehand:
- JRS: Binary Search Trees
Deliverables
To finish today's lab, make sure to do the following:
- Read through today's specs discussing more about binary trees.
- First write a depth-first iterator for Amoeba then replace with it with a breadth first iterator.
- Implement
checkthen write anisOKmethod inBinaryTree.java - Implement
fibTreeinBinaryTree.javawhich returns a fibonacci tree. - Copy the
ExprTreecode above into theBinaryTree.javafile then implementexprTreeHelperand anoptimizemethod.
You will turn in AmoebaFamily.java, and BinaryTree.java as lab13. They should still contain all your work from the previous lab as well!