A. Intro: Balancing search trees

An Overview of Balanced Search Trees

Before we begin, remember to download files using git.

Over the past couple of weeks, we have analyzed the performance of algorithms for access and insertion into binary search trees under the assumption that the trees were balanced. Informally, that means that the paths from root to leaves are all roughly the same length, and that we won't have to worry about lopsided trees in which search is linear rather than logarithmic.

This balancing doesn't happen automatically, and we have seen how to insert items into a binary search tree to produce worst-case search behavior. There are two approaches we can take to make tree balancing happen: incremental balance, where at each insertion or deletion we do a bit of work to keep the tree balanced; and all-at-once balancing, where we don't do anything to keep the tree balanced until it gets too lopsided, then we completely rebalance the tree.

In the activities of this segment, we start by analyzing some tree balancing code. Then we explore how much work is involved in maintaining complete balance. We'll move on to explore three kinds of balanced search trees: B trees, red-black trees, and splay trees.

B. Making a Balanced Tree

Exercise: Build a Balanced Tree from a Linked List

In BST.java complete the linkedListToTree method which should build a balanced binary search tree out of an already sorted LinkedList.

WARNING: This problem can trip people up. Don't spend too much time on it and come back to it at the end of the lab.

Hint: Recursion! Think about the parameters and when you need to recurse.

Hint: Draw out a couple of cases by hand and break down what needs to be done

Hint: There is only one iterator object (it will be passed through recursive calls). Think about the order things are being returned from the iterator and how to construct a tree from it!

Question: If it's a BST, why are the items just of Object type? Why not Comparable? Answer: Because you shouldn't need to ever do any comparisons yourself. Just trust that the order in the LinkedList is correct.

Self-test: linkedListToTree Runtime

Give the runtime of linkedListToTree, where N is the length of the linked list. The runtime is in:

C. B-trees

2-3-4 Trees

The first balanced search tree we'll examine is the 2-3-4 tree. 2-3-4 trees guarantee O(log(n)) height in any case. That is, the tree is always balanced by height.

2-3-4 tree are named that way because each node can have either 2, 3, or 4 children, except for the leaves. Additionally, any non-leaf node must have one more child than it does keys. That means that a node with 1 key must have 2 children, 2 keys with 3 children, and 3 keys with 4 children.

Here's an example of one:

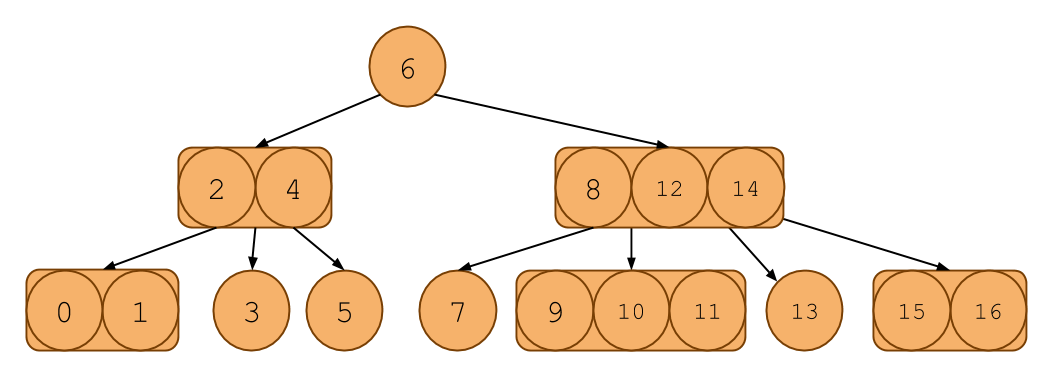
It looks like a binary search tree, except each node can contain 1, 2, or 3 items in it. Notice that it even follows the ordering invariants of the binary search tree. For example, take the [2, 4] node. Each key in the subtree rooted at the first child has items less than 2. Each key in the second subtree has items between 2 and 4. Each key in the third subtree has items greater than 4. This extends to nodes with more or less keys as well. We can take advantage of this to construct a search algorithm similar to the search algorithm for binary search trees.

Discussion: Height of a 2-3-4 Tree

What does the invariant that a 2-3-4 tree has one more child than keys tell you about the length of the paths from the root to leaf nodes? How does that keep the 2-3-4 tree balanced?

Insertion into a 2-3-4 Tree

Although searching in a 2-3-4 tree is like searching in a BST, inserting a new item is a little different.

Like a BST, we always insert the new key at a leaf node. We must find the correct place for the key that we insert to go, by traversing down the tree, then insert the new key into the appropriate place in the existing leaf. However unlike in a BST, nodes in a 2-3-4 tree can be modified as a result of insertion.

Suppose we have the following 2-3-4 tree:

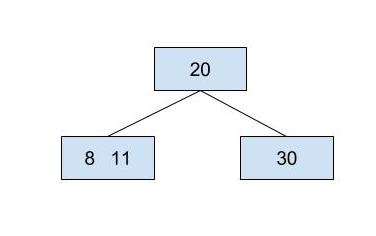
If we were to insert 10 into the tree, we first traverse down the tree until we find the proper leaf node to insert it into. We subsequently find the leaf node that contains 8 and 11. That node still has room (because a node can contain up to 3 keys), and we can insert 10 between 8 and 11, leaving us with a three key node, as shown below.

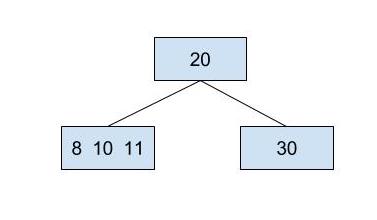
However, what if the leaf node we choose to insert into already has 3 keys? Even though we'd like to put the new item there, it won't fit because nodes can have no more than 3 keys. What should we do?

The solution is to always make sure there is room in nodes. Whenever we see a 3-key node as we walk down the tree, we will push up the middle key into the parent node. Since the parent node was visited previously and treated the same way, we are guaranteed that the parent will have space for the key we push up.

Let's try to insert 9 into the 2-3-4 tree above.

We must first do the find algorithm to determine which leaf to insert into. 9 is smaller than 20, so we go down to the left. Then we find a node with 3 keys, [8, 10, 11]. We push up the middle key (10), then split the 8 and the 11 into separate nodes. We then continue the find algorithm, going to the node with 8 (because 9 is less than 10), and insert 9 into it, as seen below.

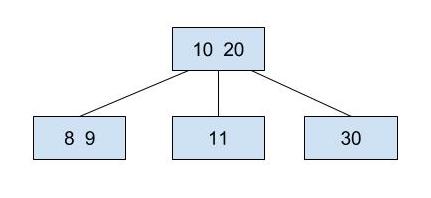
There is one little special case we have to worry about when it comes to inserting, and that's if the root is a 3-key node. Roots don't have a parent to push the middle key to. In that case, we still push up the middle key and instead of giving it to the parent, we make it the new root. Only when this happens does the height of the 2-3-4 tree increase.

Discussion

Insert 5, 7, and 12 into the 2-3-4 tree above.

Self-test: Growing a 2-3-4 Tree

Suppose the keys 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 are inserted sequentially into an initially empty 2-3-4 tree. Which insertion causes the second split to take place?

Removal from a 2-3-4 Tree

We will not be covering how to remove from a 2-3-4 tree in this course, but notes on how to do so are in JRS's notes. The idea behind removal is similar to removal from a BST. Like in insertion, we modify nodes as we find what to delete. Instead of getting rid of 3-key nodes, remove will create 3-key nodes. Again, you will not be responsible on understanding the exact mechanics of the removal algorithm.

B-trees

A 2-3-4 tree is a special case of a structure called a B-tree. What varies among B-trees is the number of keys/subtrees per node. B-trees with lots of keys per node (on the order of thousands) are especially useful for organizing storage of disk files, for example, in an operating system or database system. Since retrieval from a hard disk is quite slow compared to computation operations involving main memory, we generally try to process information in large chunks in such a situation, in order to minimize the number of disk accesses. The directory structure of a file system could be organized as a B-tree so that a single disk access would read an entire node of the tree. This would consist of, say, the text of a file or the contents of a directory of files.

D. Red-Black Trees

We have seen that 2-3-4 trees are balanced, guaranteeing that a path from the root to any leaf is O(log(n)). However, 2-3-4 trees are notoriously difficult and cumbersome to code, with numerous corner cases for common operations.

What's used in practice is a Red-Black tree (in fact it is the tree behind Java's TreeSet and TreeMap). A Red-Black tree is a usual binary search tree, but has additional invariants related to "coloring" each node red or black. This in fact creates a mapping between 2-3-4 trees and Red-Black trees!

The consequence is quite astounding: Red-Black trees maintain the balancedness of B-trees while inheriting all normal binary search tree operations (a Red-Black tree IS a binary search tree) with additional housekeeping. This self-balancing quality is why Java's java.util.TreeMap and java.util.TreeSet are implemented as Red-Black trees!

2-3-4 tree ↔ Red-Black tree

Notice that a 2-3-4 tree can have 1, 2, or 3 elements per node, and 2, 3, or 4 pointers to its children. Consider the following 2-3-4-tree node:

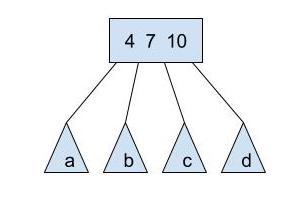
a, b, c, and d are subtrees. a will have elements less than 4, b will have elements between 4 and 7, c will have elements between 7 and 10, and d will have elements greater than 10.

Let us transform this into a "section" in Red-Black tree that represents above node:

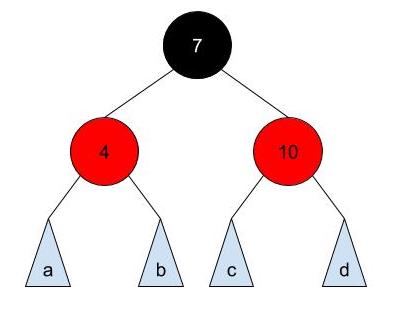
For each node in 2-3-4 tree, we have a group of normal binary search tree nodes (augmented with colors) that correspond to it:

• Middle element ↔ black node that is reachable from parent.
• Left element ↔ red node on the left of the black node.
• Right element ↔ red node on the right of the black node.

Notice that a, b, c, and d are also "sections" that corresponds to a 2-3-4 tree node. Thus, the subtrees will have black root nodes.

How about a 2-3-4 node with two elements?

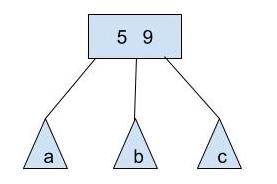
This node can be transformed as either :

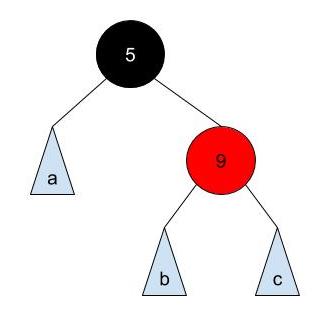
or

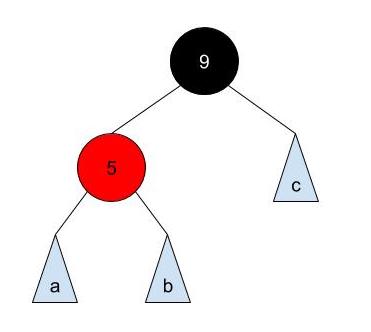
Both are valid.

Trivially, for 2-3-4 node with only one element, it will translate into a single black node in Red-Black tree.

A Red-Black tree is balanced in terms of black nodes. Although it is not as balanced as a 2-3-4 tree, because of the way that is is translated from a 2-3-4 tree, the number of black nodes on any path from the root to a leaf will be the same.

Exercise:

Read the code in RedBlackTree.java and BTree.java. Then, in RedBlackTree.java, fill in the implementation for buildRedBlackTree which returns the root node of the Red-Black tree which has a mapping to a given 2-3-4 tree. For 2-3-4 tree node with 2 elements in a node, you must use the left element as the black node to pass the autograder tests. For the example above, you must use the first representation of Red-Black tree where 5 is the black node.

Hint: It may be helpful to do think recursively.

Hint: Pay attention to the drawings above when coding this up.

Red-Black trees are Binary Search Trees

As stated above, Red-Black trees are still binary search trees: a left subtree for a node contains all elements less than the node's and the same holds for the right subtree.

Discussion

For the following operations, discuss with your partner about which of the following binary search tree operations we can use on Red-Black trees without any modification.

1. Insertion
2. Deletion
3. Search (is k in the tree?)
4. Range Queries (return all items between a and b)

Red-Black Tree Insertion and Deletion

Red-Black trees maintain their balance through rotations (which we will discuss in depth in a moment with splay trees) and recoloring operations. The actual algorithms for both are tedious (5 cases to consider for insertion, 6 cases for deletion), and in the interest of time, we will not discuss them in depth here. However, because of the fact that there is a correspondence between Red-Black trees and 2-3-4 trees, we can transform a Red-Black tree into a 2-3-4 tree, insert into it, and then transform is back into a Red-Black tree.

E. Splay Trees

The next balanced search tree we will discuss is the splay tree. Unlike 2-3-4 trees and Red-Black trees, there is no guarantee of balance. However, splay trees have an amortized logarithmic runtime. Splay trees have some advantages over 2-3-4 trees and Red-Black trees. Structurally, it is exactly like a BST and does not require any extra bookkeeping information. Because of its simplicity, insertions and deletions can be faster in practice.

Splay trees are designed to give especially fast access to entries that have been accessed recently, so they really excel in applications where a small fraction of the etnries are the target of most of the find operations. This is called locality of reference. For many real world data sets and uses, this will end up being the case.

Rotations

Like a Red-Black tree, splay trees are kept balanced through rotations, which change the structure of the tree.

Consider the following tree:

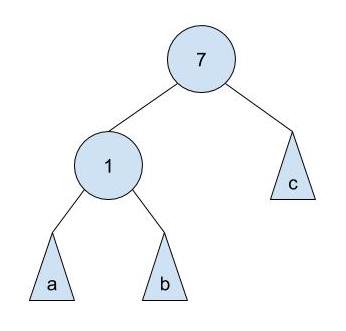
a is a subtree with all elements less than 1, b is a subtree with elements between 1 and 7, and c is a subtree with all elements greater than 7. Now, let's take a look at another tree:

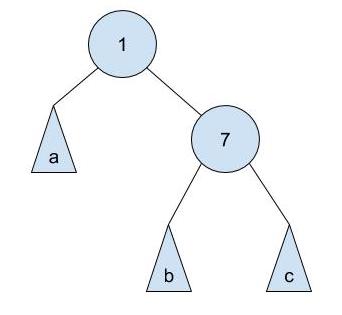
There are few key things to notice:

1. The root of the tree has changed from 7 to 1.
2. a, b, and c are still correctly placed. That is, their items do not violate the binary search tree invariants.
3. The height of the tree can change by 1.

Here, we call this transition from the first tree to the second a "right rotation on 1 through 7".

Now, convince yourself that a "left rotation on 7 through 1" on the second tree will give us the first tree. The two operations are symmetric, and both maintain the binary search tree property!

Discussion: Rotation by Hand

We are given an extremely unbalanced binary search tree:

    0
     \
      1
       \
        3
       / \
      2   6
         / \
        4   8

Write down a series of rotations (i.e. rotate right on 2 through 3) that will make tree balanced and have height of 2. HINT: Two rotations are sufficient.

Exercise: Rotation Implementation

Now we have seen that we can rotate the tree to balance it without violating the binary search tree invariants. Now, we will implement it ourselves! In SplayTree.java, implement rotateRight and rotateLeft.

Hint: The two operations are symmetric. Should the code significantly differ? Hint: Rotations can be done with just pointer manipulations. Look at the figures above and see what pointers are changed. Hint: Remember to set parent pointers

Splaying

Splay Trees get their name from the splay operation that it uses. Given a node x, we splay x by making it the root of the tree through rotations. Why? This is so that recently accessed entries are near the root of the tree, which means if we access the same few entries repeatedly, accesses will be very fast. Another reason is that if x is down an unbalanced spindly branch of the tree, splaying x will improve the balance along that branch.

Splaying depends on the relative positions of x, its parent p, and its grandparent g (if it exists). There are three cases that determine the rotations that we use.

1. zig-zag: if x is the right child of a left child, we first rotate x left through p and then rotate x right through g.

   The symmetric case where x is the left child of a right child uses the same rotations in mirror image: first rotate x right through p and then rotate left through g.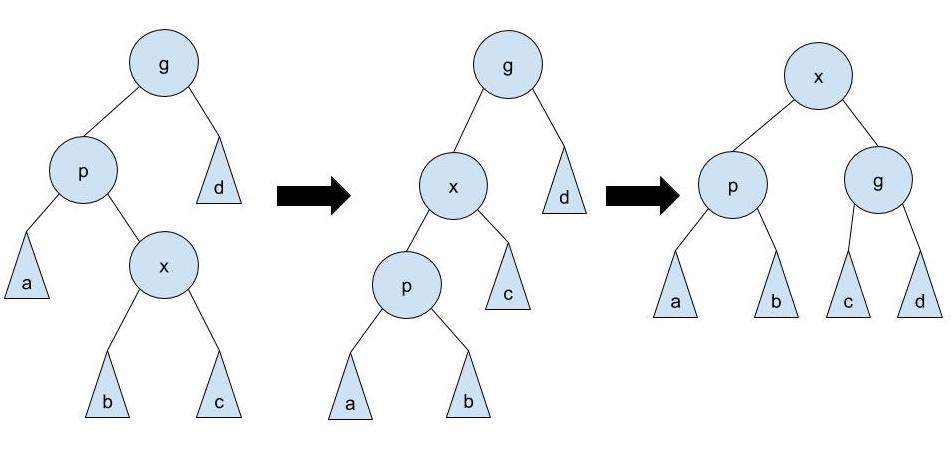

   

2. zig-zig: if x is the left child of a left child, the order of the rotations is reversed from the first case. We first rotate p right through g and then rotate x right through p

   The symmetric case where x is the right child of a right child uses the same rotation in mirror images: rotate p left through g, then x left through g.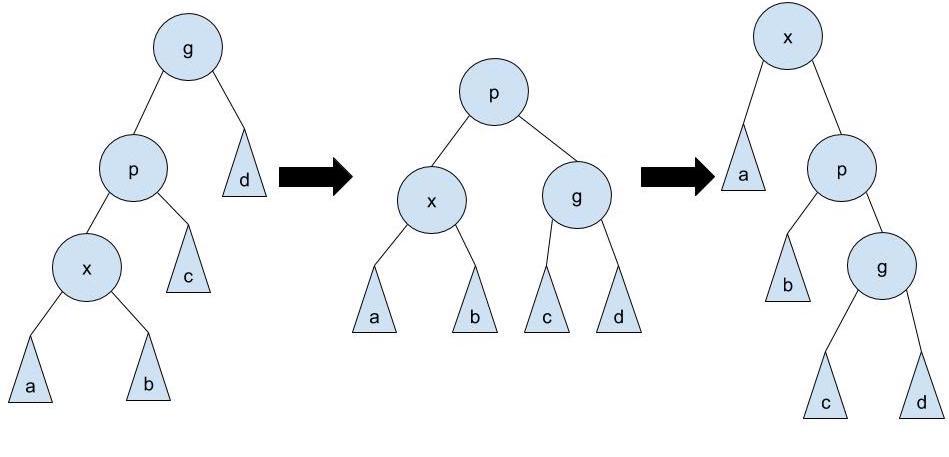

   

3. zig: if x is a child of the root, we rotate x through p so that x becomes the root.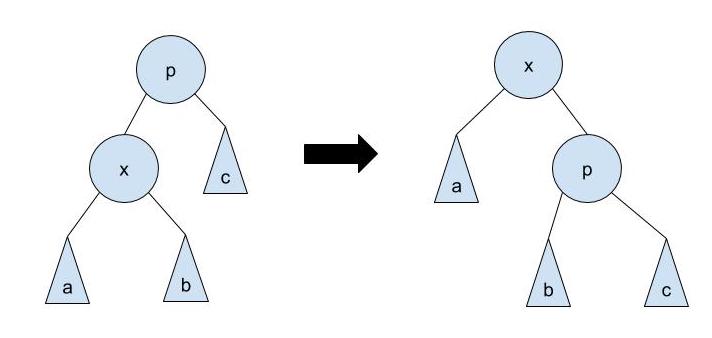

   

We repeatedly apply zig-zag and zig-zig operations to x. Each operation will raise x up two levels in the tree. Eventually it will become the root, or it will be the child of the root, in which case we zig.

Through these operations, a node initially at depth d on the path from the root to x will move to a final depth no greater than 3 + d/2. That means that all nodes deep down the search path will have their depths roughly halved. This tendency prevents a splay tree from staying unbalanced for long.

Exercise:

Now, we will implement zig, zigzag, and zigzig, methods in SplayTree.java. We have already implemented splayNode for you.

Hint: These methods should be very short.

Hint: Remember the symmetric cases!

Splay Tree Operations

Operations on a splay tree are exactly like the operations in a regular BST. However a splay tree is not done there. We must splay a node to the root.

1. get(K key): Just like in a BST, we traverse down the tree to find the node that contains the key. Let x be the node that the search algorithm terminates at (which may or may not contain the key, depending on if the tree contains the key in the first place). We then splay x to the root of the tree.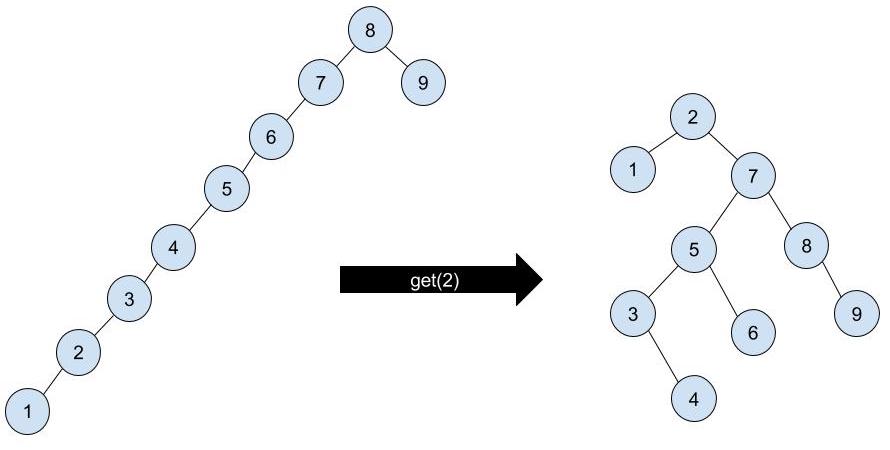

   

2. put(K key, V value): We insert the new entry containing (K, V) just as in a regular BST. We then splay the new node we created to the root.

3. remove(K key): We will remove the node that contains the key from the tree following the normal deletion algorithm for a BST. Let x be the node that we remove. We then splay x's parent to the root. If the key is not in the tree, just like in a get operation, we splay the node where the search ended.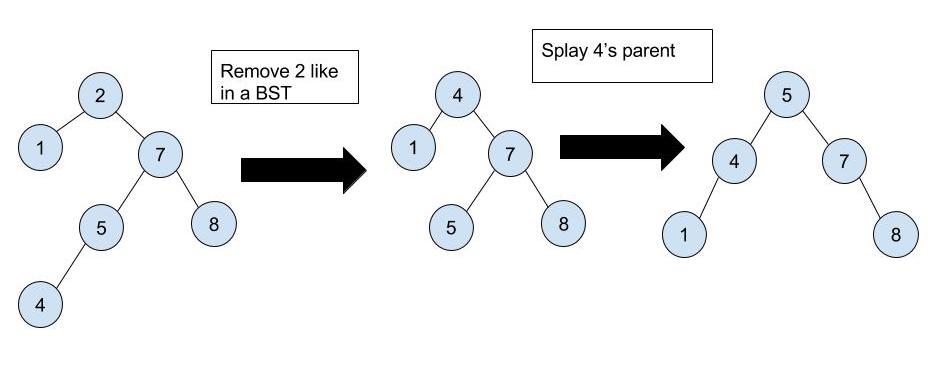

   

We have provided the implementations for get and put. Make sure that you understand the operations and when we splay.

F. Other Balanced Trees

AVL Trees

AVL trees (named after their Russian inventors, Adel'son-Vel'skii and Landis) are height-balanced binary search trees, in which information about tree height is stored in each node along with the item. Restructuring of an AVL tree after insertion is done via a familiar process of rotation, but without color changes.

Left-Leaning Red-Black Trees

A variant on Red-Black trees are Left-Leaning Red-Black Trees (LLRBTs), where only left children can be red nodes. This simplifies many of the conditions and the code of a normal Red-Black tree. LLRBTs have an isometry with 2-3 trees (a variant on 2-3-4 trees where a node can only have 2 or 3 children, except for leaves).

G. Conclusion

Summary

We hope enjoyed learning about balanced search trees. They can be a bit tricky to implement compared to a normal BST, but the speedup in runtime helps us immensely in practice! Now that you've seen them, hopefully you can appreciate the work that went into Java's TreeMap and TreeSet that you can use as a black box.

Submission

Please turn in RedBlackTree.java, SplayTree.java, and BST.java.