A. Intro

Today, we'll be continuing our discussion of data structures. First, we'll explore how we can actually represent a tree using a simple array. Next, we'll take a look at an important abstract data type, the priority queue, and how it can be implemented using a heap. We'll close by taking a closer look at the heap data structure and its uses in various algorithms.

Download the code for Lab 18 and create a new IntelliJ project out of it.

B. Representing a tree with an array

You've seen two approaches to implementing a sequence data structure: either using an array, or using linked nodes. We extended our idea of linked nodes to implement a tree data structure. It turns out we can also use an array to represent a tree.

Here's how we implement a binary tree:

• The root of the tree will be in position 1 of the array (nothing is at position 0; this is to to make indexing more convenient). We can define the position of every other node in the tree recursively:
• The left child of a node at position $n$ is at position $2n$.
• The right child of a node at position $n$ is at position $2n + 1$.
• The parent of a node at position $n$ is at position $n/2$.

Self-test: ArrayBST Representation

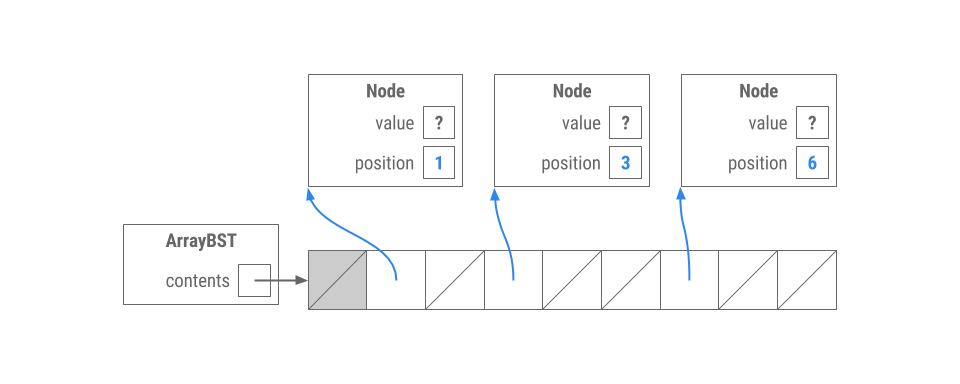
Suppose we have a class ArrayBST which implements a BST in the way described above.

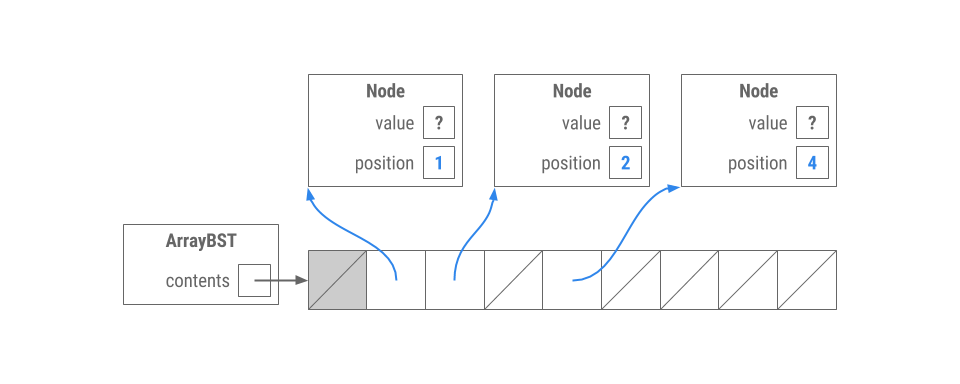
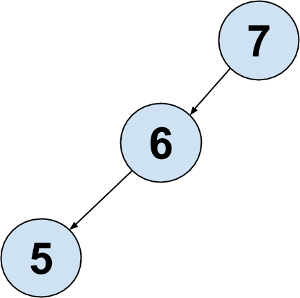
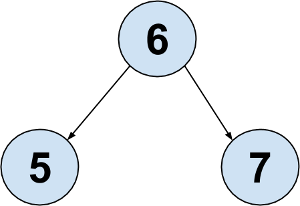
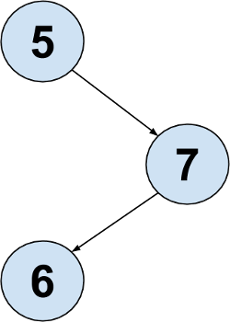
Which of the following trees could be represented by the ArrayBST shown above? (The values have been omitted and replaced with ?s)

Option 1	Option 2	Option 3	Option 4

Choose one answer.

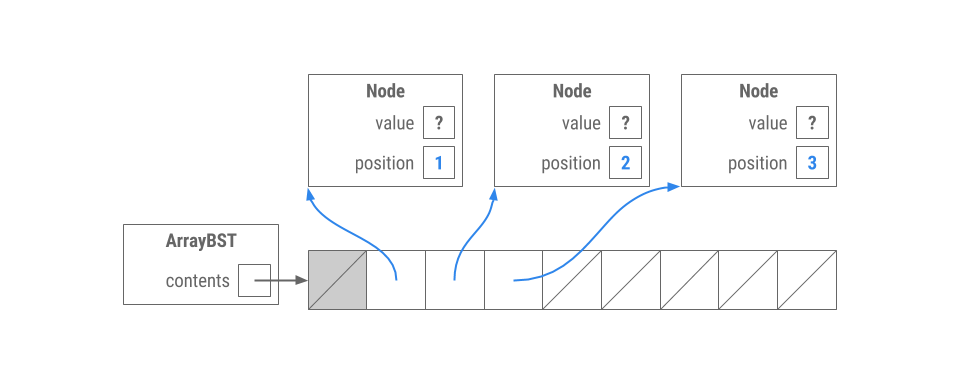
Now we have a new ArrayBST:

Which of the trees could represent it? Choose one answer.

Now suppose we have this ArrayBST:

Self-test: a Naive BST contains

In ArrayBST, the underlying collection that stores pointers to the node objects is an ArrayList contents. Code for the contains method appears below.

public boolean contains (int value) {
    for (Node treeNode : contents) {
        if (treeNode != null && treeNode.value == value) {
            return true;
        }
    }
    return false;
}`

The contains method runs in time proportional to what in the worst case?

How would you rewrite the contains method in ArrayBST to run in time proportional to the height of the tree?

C. Implementations of queues and priority queues

Stacks, Queues and Priority Queues

A stack is a last-in-first-out (LIFO) abstract data type; much like a physical stack, one can only access the top of the stack and must pop off recently added elements to retrieve previously added elements. Imagine a stack of plates: we can only remove the plate we last added. Stacks are often used for graph algorithms based on Depth-First-Search (which we'll cover later in this course) and recursion (remember the stack and heap diagrams from lab2?).

Today, we're more interested in the queue, which is a first-in-first-out (FIFO) abstract data type. Recall that a queue also acts like its namesake: when we process items in a queue, we process those added most recently last. Imagine a queue of people waiting in line: the first person to enter the queue is also the first person to leave the queue. Queues are often used for graph algorithms based on Breadth-First-Search (which we saw when implementing a tree iterator).

Sometimes, however, processing items in the order they arrive is not what we want to do. We may instead want to process items in order of importance or a priority score. Enter the priority queue...

Queues and priority queues can be implemented by many different data structures, but all have the same operations:

• construct an empty queue
• enqueue: add an element to the queue
• dequeue: remove an element from the queue (for a normal queue, this is the oldest element in the queue. For a priority queue, this is the one with most priority)
• isEmpty: check if the queue is empty
• peek: get the item at the front of the queue without removing it

Traditionally, Black Friday lines are like a queue. People are served based on the order they arrive, regardless of what they want to buy.

An emergency room is like a priority queue. The people waiting with the most pain are served first, regardless of when they arrived.

Why this is important: Priority queues are an integral component of many algorithms for graph processing (which we'll cover in a few labs). For example, the first few weeks of CS 170 typically involve graph algorithms that use priority queues. Look out for priority queues in other CS classes as well -- for example, you'll find them invaluable in the operating systems class CS 162, where they're used to schedule which processes in a computer to run at what times.

Self-test: Runtimes of Different Priority Queue Implementations

For the following examples, we will prioritize items with the smallest value first (assuming the items are Comparable). Note that you can create a priority queue with your own custom priority by using the following priority queue constructor: PriorityQueue(int initialCapacity, Comparator<? super E> comparator).

Consider the implementation of a priority queue with an unordered linked list of $N$ elements, and complete the following sentence:

In the worst case, the run time to insert something into the priority queue is in...

Consider the implementation of a priority queue with an unordered linked list of $N$ elements, and complete the following sentence:

In the worst case, the run time to remove the element with highest priority is in...

Consider the implementation of a priority queue with an ordered linked list of $N$ elements, and complete the following sentence:

In the worst case, the run time to insert something into the priority queue is in...

Consider the implementation of a priority queue with an ordered linked list of $N$ elements, and complete the following sentence:

In the worst case, the run time to remove the element with highest priority is in...

Consider the implementation of a priority queue with a balanced binary search tree of $N$ elements, and complete the following sentence:

In the worst case, the run time to insert something into the priority queue is in...

Consider the implementation of a priority queue with a balanced binary search tree of $N$ elements, and complete the following sentence:

In the worst case, the run time to remove the element with highest priority is in...

Queue and PriorityQueue in java.util

The java.util library contains a Queue interface and a PriorityQueue class that implements Queue. Queue methods include the following:

• offer(element), which adds the element to the queue (this is enqueue)
• peek(), which returns but does not remove the head of the queue
• poll(), which retrieves and removes the head of the queue (returning null if the queue is empty) (this is dequeue)

Java's priority queue is implemented with a data structure called a binary min heap. In the rest of this lab, you will study and implement this data structure yourself.

D. Binary heaps

Binary Heaps Intro

Having a fast implementation of a priority queue would be very helpful, but as we saw in the last exercise, the most obvious implementations each have flaws. Enter the binary heap. The binary heap is a data structure that will help us implement a priority queue with fast operations. We want to be able to quickly insert objects into the heap with different priority values, and we want to be able to quickly remove the most important item.

There are two flavors of binary heaps: min heaps and max heaps. They're very similar except the former organizes items by smallest, and the latter organizes items by largest. Choose either one depending on your definition of priority score.

In these labs we may work with either a max or min heap. It should be easy to figure out how the other one works by example. But pay attention so you don't get confused by which one we're using!

Summary: Understand the difference between priority and priority values. For both heaps, higher priority items appear at the top of the heap. However, in min heaps, items with smaller priority values have higher priority. In max heaps, items with larger priority values have higher priority. This is an important distinction to understand. Keep this in mind as you read through and implement the rest of this lab.

Binary Heaps Defined

Binary min heaps are basically just binary trees (but not binary search trees) --- they have all of the same invariants of binary trees --- with two extra invariants:

• Invariant 1: the tree must be complete (more on this later)
• Invariant 2: The priority value of some node must be smaller than that of its children. This is the min-heap property (there is another variation called the max-heap property where the reverse is true: the priority value of every node is larger than its children)

Invariant 2 guarantees that the element with the lowest priority value (and, therefore, the highest priority) will always be at the root of the tree. This helps us access that item quickly, which is what we need for a priority queue.

For the rest of this spec, we will be discussing operations in terms of min heaps.

Complete Trees

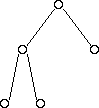
There are a couple different notions of what it means for a tree to be well balanced. A binary heap must always be what is called complete.

A complete tree:

• Has all available positions for nodes filled, except for possibly the last row, which must be filled left-to-right

Below are some examples of trees that are complete:

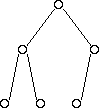
And some examples of trees that are not complete:

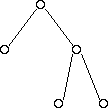
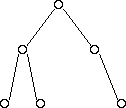
Operations

There are three operations that we care about: adding to the heap, removing the item with the highest priority (in a min heap, this is the item with the lowest priority value), and getting the highest priority item. When we do these operations, we need to make sure to maintain the above invariants (completeness and min/max-heap). Here's how we do it:

Getting the item with the smallest priority value

The item with the smallest priority value will always be stored at the root. Thus, we can just return the root node, without changing the structure of the heap (this is similar to the peek operation in queues).

Add an item

1. Put the item you're adding in the next available spot in the bottom row of the tree. If the row is full, make a new row (this ensures the completeness of the tree)
2. Swap the item you just added with its parent while its priority value is smaller than its parent, or until it is the new root. This is called bubbling up. (This ensures the min-heap property)

Remove the item with min priority value

1. Replace the item at the root with the item in the rightmost spot of the bottom row (again maintaining the completeness).
2. Bubble down the new root until its priority value is smaller than both its children. If you reach a point where you can either bubble down through the left or right child, you must choose the smaller of the two (this ensures the min-heap property is maintained).

Play with Heaps

We just covered a lot of new concepts for heaps. To test yourself and see if you understand them, try drawing a heap. Draw what happens when you insert numbers into the heap and when you decide to remove the smallest (or biggest) one.

Also, check out this interactive animation of a min heap. You can type in numbers to insert, or remove the min element (ignore the BuildHeap button for now; we'll talk about that shortly). You can use this animation to check your own drawings too -- there is no ambiguity when constructing heaps, so if you insert numbers in the same order, yours should look exactly the same as this animation.

Exercise: Implementing your own heap

The class ArrayHeap implements a binary min heap using an ArrayList, just like we discussed at the beginning of this lab. Open it up and read the provided methods.

What is the purpose of contents.add(null) in the constructor?

Fill in the missing methods in ArrayHeap.java.

• As John DeNero wisely says, code that doesn't respect abstraction barriers should BURN. Respect abstraction barriers! That is, when you implement insert, removeMin, and changePriority, you should be using bubbleUp and/or bubbleDown, and when you implement bubbleUp and bubbleDown, you should be using getLeft, getRight, and/or getParent.
• You should be able to work on the methods in order. The first couple are relatively easier. Don't forget to write a suite of JUnit tests to test your code.

E. Binary heap brainteasers

Self-test: Heaps and BSTs

Consider binary trees that are both max heaps and binary search trees.

How many nodes can such a tree have? Check all that apply.

Self-test: Determining if a Tree is Complete

It's not obvious how to verify that a linked binary tree is complete. A CS 61BL student suggests the following recursive algorithm:

1. A one-node tree is complete.
2. A tree with two or more nodes is complete if its left subtree is complete and has depth $k$ for some $k$, and its right subtree is complete and has depth $k$ or $k - 1$.

Here are some example trees. Think about whether or not the student's proposed algorithm works correctly on them.

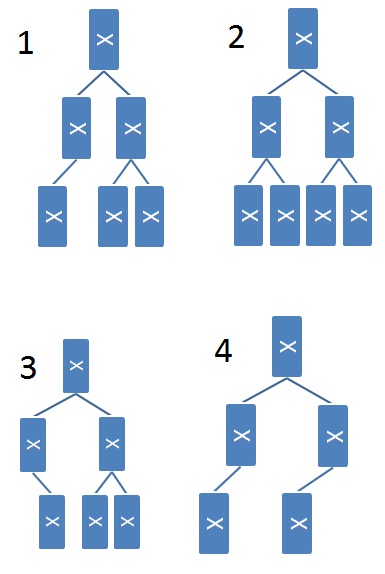
Check all that apply to test your understanding of the proposed algorithm.

Discussion: Complete Trees and BFS

Another CS 61BL student claims that a binary tree is complete if all the leaves in the tree come at the end of a breadth-first traversal of the tree. Give a counterexample to this claim.

Self-test: The Third Biggest Element in a Max Heap

Here's an example heap.

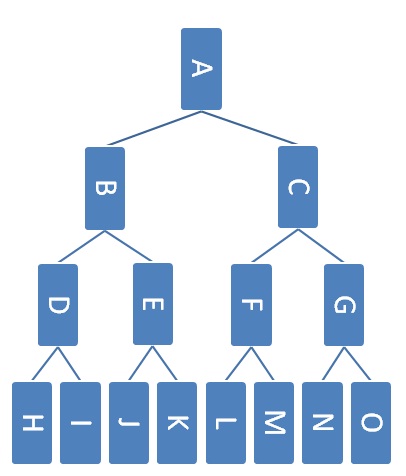
Which nodes could contain the third largest elements in the heap assuming that the heap does not contain any duplicates?

Which nodes could contain the third largest elements in the heap assuming that the heap can contain duplicates?

F. More with Binary Heaps

Heapsort

Suppose you have an array of $N$ numbers that you want to sort smallest-to-largest. One algorithm for doing this is as follows:

1. Put all of the numbers in a min heap.
2. Repeatedly remove the min element from the heap, and store them in an array in that order.

This is called heapsort.

Since each insertion takes proportional to $\lg N$ comparisons once the heap gets large enough, and each removal also takes proportional to $\lg N$ comparisons, the whole process takes proportional to $N \log N$ comparisons.

It turns out we can actually make step 1 of heapsort run faster -- proportional to $N$ comparisons --- using a process called heapify. (Unfortunately, we can't make step 2 run any faster than $N \log N$, so the overall heapsort must take $N \log N$ time.)

Heapify

The algorithm for taking an arbitrary array and making it into a min (or max) heap in time proportional to $N$ is called heapify. Pseudocode for this algorithm is below:

def heapify(array):
    index = N/2
    while index > 0:
        bubble down item at index
        index--

Conceptually, you can think of this as building a heap from the bottom up. To get a visualization of this algorithm working, click on the BuildHeap button on the animation we linked earlier. This loads a pre-set array and then runs heapify on it.

It is probably not immediately clear to you why this heapify runs in $O(N)$. For those who are curious, you can check out an explanation on Wikipedia or section 9.3.4 of the DSA textbook.

Finding the K Largest Elements

In the following problem you will reason about an algorithm that collects the $k$ largest elements in a list of length $N$. For this problem, let the priority value of any element be the value of the element itself (e.g. if we are working with Integers, then 3 will have a priority value of 3). Before you look at the questions, try to design an algorithm that could accomplish this in the asymptotically least amount of time.

You can use a heap to solve this problem. How large of a heap would you need?

Choose one answer.

What type of heap would be best to use?

Choose one answer.

What would the run-time be proportional to for this algorithm?

Choose one answer.

This is a tricky algorithm! If you still can't picture how it works, draw out the heap, add all the list elements to it, and see what happens.

G. Conclusion

Submission

Submit ArrayHeap.java.