A. Intro

There will be no new skeleton files for this lab. Locate your Graph.java file from the last lab, copy and paste it into lab20 directory, and create an IntelliJ project out of it.

B. More Graph Traversal Algorithms

Review of Traversal-Based Algorithms

Last lab, you were introduced to graphs and their representations, then moved on to basic graph iteration. A variety of algorithms for processing graphs are based on this kind of iteration. We've already seen two of them:

• Determining if a path exists between two different vertices
• Topological sorting

Neither algorithm depended on the representation of the fringe. Either depth-first traversal (using a stack) or breadth-first traversal (using a queue) would have worked.

We're now going to investigate an algorithm where the ordering of the fringe does matter. But first:

Keep Track of Extra Information

Recall the exercise from last lab where you located a path from a "start" vertex to a "stop" vertex. A solution to this exercise involved building a traversal, then filtering the vertices that were not on the path. Here was the suggested procedure:

"... Then, trace back from the finish vertex to the start, by first finding a visited vertex u for which (u, finish) is an edge, then an earlier visited vertex v for which (v, u) is an edge, and so on, finally finding a vertex w for which (start, w) is an edge. Collecting all these vertices in the correct sequence produces the desired path."

If each fringe element contains a vertex and its predecessor along the traversed path, we can make the construction of the path more efficient. Instead of searching for the previous vertex along the path, we merely follow the predecessor links. This is an example where it is useful to store extra information in the fringe along with a vertex.

Associating Distances with Edges

In graph applications we've dealt with so far, edges were used only to connect vertices. A given pair of vertices were either connected by an edge or they were not. Other applications, however, process edges with weights, which are numeric values associated with each edge. Remember that in an application, an edge just represents some kind of relationship between two vertices, so the weight of the edge could represent something like the strength or weakness of that relationship.

In today's exercises, the weight associated with an edge will represent the distance between the vertices connected by the edge. In other algorithms, a weight might represent the cost of traversing an edge or the time needed to process the edge.

A graph with edge weights is shown below.

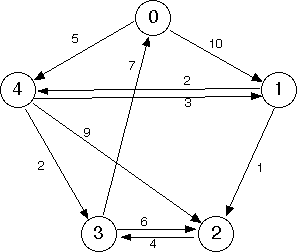
Observe the weights on the edges (the small numbers in the diagram), and note that the weight of an edge (v, w) doesn't have to be equal to the weight of the edge (w, v) (its reverse).

Shortest Paths

A common problem involving a graph with weighted edges is to find the shortest path between two vertices. This means to find the sequence of edges from one vertex to the other such that the sum of weights along the path is smallest.

A real life application of this is what online map software does for you. Say you want directions from one location to another. Your mapping software will try to find the shortest path from your location (a vertex), to another location (another vertex). Different paths in the graph may have different lengths and different amounts of traffic, which could be the weights of the paths. You would want your software to find the shortest, or fastest, path for you.

Self-test: Finding a Shortest Path

Given below is the graph from the previous step.

Suppose that the weight of an edge represents the distance along a road between the corresponding vertices. (A distance might not be the same going, say, north to south as in the opposite direction.) The weight of a path would then be the sum of the weights on its edges.

What is the shortest path—the one with the minimum distance sum—that connects vertex 0 with vertex 2?

Dijkstra's Shortest Path Algorithm

How did you do on the shortest path self-test? It's pretty tricky, right? Luckily, there is an algorithm devised by Edsger Dijkstra (usually referred to as Dijkstra's Algorithm), that can find the shortest paths between two vertices in a graph. Actually, it's tedious for humans to do by hand, but it isn't too inefficient for computers.

Below is an overview of the algorithm. Note: The algorithm below finds the shortest paths from a starting vertex to all other nodes in a graph (otherwise known as a shortest paths tree). To find the shortest path between two specified vertices s and t, simply terminate the algorithm after t has been visited.

Initialization:

1. Maintain a mapping, from vertices to their distance from the start vertex. This will be used by the fringe to determine the next vertex to visit.
2. Add the start vertex to the fringe with distance zero.
3. All other nodes can be left out of the fringe. If a node is not in the fringe, assume it has distance infinity.
4. For each vertex, keep track of which other node is the predecessor for the node along the shortest path found.

While-Loop

Loop until the fringe is empty.

1. Remove and hold onto the vertex v in the fringe for which the distance from start is minimal. (One can prove that for this vertex, the shortest path from the start vertex to it is known for sure.)
2. If v is the destination vertex (optional), terminate now. Otherwise, mark it as visited; likewise, any visited vertices should not be visited again.

3. Then, for each neighbor w of v, do the following:

   1. As an optimization, if w has been visited already, skip it (as we have no way of finding a shorter path anyways)
   2. If w is not in the fringe (or another way to think of it - it's distance is infinity or undefined in our distance mapping), add it to the fringe (with the appropriate distance and previous pointers).
   3. Otherwise, w's distance might need updating if the path through v to w is a shorter path than what we've seen so far. In that case, replace the distance for w's fringe entry with the distance from start to v plus the weight of the edge (v, w), and replace its predecessor with v. If you are using a java.util.PriorityQueue, you will need to call add or offer again so that the priority updates correctly - do not call remove as this takes linear time.

Every time a vertex is dequeued from the fringe, that vertex's shortest path has been found and it is finalized. The algorithm ends when the stop vertex is returned by next. Follow the predecessors to reconstruct the path.

One caveat: Although we often use the analogy of finding the shortest path in a map to describe Dijkstra's algorithm, note that it's possible to try to run Dijkstra's on any arbitrary graph structure. This means you may come across a graph with negative edge weights. For instance, consider a real-life example graph where the vertices are the locations. As a taxi driver, you are paid to drive customers between certain locations. However, you may lose money when you drive to pick up a new customer. In fact, Dijkstra's algorithm may not work in general on such graphs with negative edge weights! Consider why this is the case. You'll learn about alternatives in CS 170 (if you're very curious now, feel free to look up the Bellman-Ford algorithm, although you certainly are not responsible for this knowledge in 61BL).

Dijkstra's Algorithm Animation

Dijkstra's algorithm is pretty complicated to explain in text, so it might help you to see an animation of it. Here's a Youtube video that goes through an example of Dijkstra's algorithm using a similar implementation as the one we use in this class. Check it out if you want to see a visual of the algorithm (or likely, your TA has already demonstrated it!).

Note that in this video, he initializes the fringe by putting all the vertices into it at the beginning with their distance set to infinity. While this is also a valid way to run Dijkstra's algorithm for finding shortest paths (and one of the original ways it was defined), this is inefficient for large graphs. Semantically, it is the same to think of any vertex not in the fringe as having infinite distance, as a path to it has not yet been found.

Discussion: Dijkstra's Algorithm Animation

• In the animation you just watched, how can you tell what vertices were currently in the fringe for a given step?
• In the animation you just watched, after the algorithm has been run through, how can you look at the chart and figure out what the shortest path from A to H is?

Exercise: A Sample Run of Dijkstra's Algorithm

Run Dijkstra's algorithm by hand on the pictured graph below, finding the shortest path from vertex 0 to vertex 4. Keep track of what the fringe contains at every step.

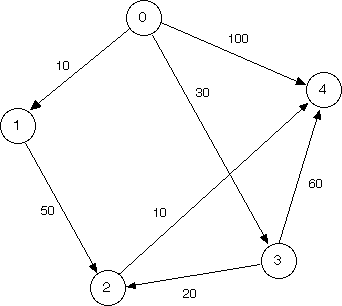
We recommend keeping track of a table like in the animation. Also, please make sure you know what the fringe contains at each step.

Exercise: Code Dijkstra's

Add Dijkstra's algorithm to Graph.java from yesterday. Here's the method header:

public ArrayList<Integer> shortestPath (int startVertex, int endVertex) {
    //your code here...
}

For this method, assume that each edge in the graph has a weight field that is a positive Integer. This will be represented by the Edge object's edgeInfo field.

It may be useful to write a getEdge method, that will return the Edge object corresponding to the input variables. Here's the header:

public Edge getEdge(int u, int v) {
    //your code here...
}

Hint 1: At a certain point in Dijkstra's algorithm, you have to change the value of nodes in the fringe. Java's priority queue does not support this operation directly, but you can add a new entry into the priority queue that contains the updated value (and will always be dequeued before any previous entries). Then, by tracking which nodes have been visited already, you can simply ignore any copies after the first copy dequeued.

Hint 2: Adding the vertices to our priority queue fringe directly won't be enough. Our vertices are Integers, so our priority queue will order them by their natural ordering. Is this what we want? If not, is there a way we can change how to order the items in the priority queue?

Runtime

Implemented properly using a binary heap, Dijkstra's algorithm should run in O((|V| + |E|) log |V|) time. This is because at all times our heap size remains a polynomial factor of |V| (even with lazy removal, our heap size never exceeds |V|^2), and we make at most |V| dequeues and |E| updates requiring heap operations.

For connected graphs, the runtime can be simplified to O(|E| log |V|), as the number of edges must be at least |V|-1. Using alternative implementations of the priority queue can lead to increased or decreased runtimes.

C. Other Graphs

Graph Applications

In the remainder of that lab we're going to be going over a couple of cool applications of graphs in the real world that might be familiar to you. But first, respond to the following discussion.

Discussion: Generic Graphs?

Remember the two graph data structures we introduced earlier: the adjacency matrix and the array of adjacency lists. Both of these made sense for graphs where the vertices were nonnegative integers, since we used the vertices to index into the matrix or the array.

What should we do if we want our graph to have vertices that are something else -- like strings, or other objects? Discuss one approach to solving this problem (there is more than one reasonable approach).

D. The Internet as a Graph

Vertices and Edges of the Internet

The World Wide Web can be viewed as directed graph in which the vertices are static pages, and two vertices are connected by an edge if one page contains a hyperlink to the other. A very small slice of the Internet appears below.

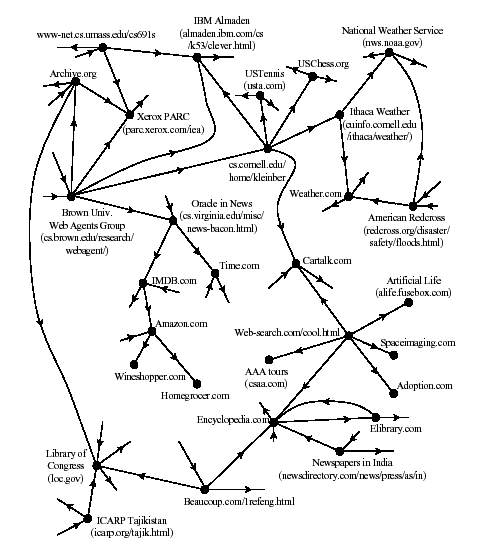
This is a very large graph. In 2001, there were estimated to be over four billion web pages. As of 2014, estimates on the size of the web vary wildly, and some have reached as high as at least one trillion.

The shape of the web

Most agree that a very large portion of the Internet is a strongly connected core of web pages, all of which are reachable from one another by following links. The majority of web sites you visit probably have pages in this core. However, it is also known that a significant portion of the Internet is made up of pages that are not a part of this strongly connected core, though the number and nature of these pages remains a topic of debate.

Web Crawlers and Search Engines

A web crawler is a program that traverses the graph that is the Internet, looking for "interesting" pages to index. A search engine takes a query and presents pages from the index, with the most "interesting" ones first.

The index is a massive table; the keys are the content words, and the values are the associated URLs. The crawler adds pages to the table, and the search engine retrieves them. The crawler must also maintain a second table to know what pages it has visited already.

Of course, this is a simplified explanation of how search engines work, but hopefully you can see how the data structures we've studied in this class apply.

Discussion: A Web Crawler's Table of Already Visited Web Pages

The table of already-visited pages used by the crawler has to be a hash map, not a hash set. Explain why, and say what value would be associated with a given key.

How Web Crawlers Define "Interesting"

A Web crawler isn't able to search the whole web; it's just too big. A user often finds that listings are three or four months out of date. The best indexes cover only around 25% of the accessible pages. Thus there is an incentive to maximize the "bang for the buck" by visiting only those pages that are likely to yield interesting elements of the index.

The search engine faces a similar problem when answering a query. There may be an enormous number of indexed pages that are possibly relevant to the query, and the search engine has to order them so that the most interesting pages get presented to the user first.

"Interesting" was traditionally defined by content. For example, a page might be evaluated according to how many "interesting" words it contained. On the search engine side, a page might be evaluated according to the position of the query words in the page (nearer the beginning is better), on the number of times previous users have accessed that page, or on the "freshness" or recency of the page. Soon, however, users seeking to maximize exposure to their pages uncovered ways to trick the content evaluation. For example, they would include many invisible copies of a popular keyword in their pages.

The big innovation of Google's inventors Larry Page and Sergey Brin (former Stanford grad students) was to include properties of the graph structure in the test for interestingness. Initially they gave priority to pages with higher in-degree, on the assumption that the more people that link to your page, the better your page must be. They later refined that idea: the more interesting pages link to you, the more interesting you must be. Web crawlers can use the same criterion to tell whether to continue their search through a given page.

Discussion: Think about a Way to Fool "Interestingness" Criteria

One reason for not just tallying in-degrees of pages was that devious users found a way to fool the system. Describe a way to design a Web site to make the pages look more "interesting", where "interesting" means "having a higher in-degree".

Improving Crawler/Search Engine Performance

Improving the performance of web crawlers and search engines is a thriving area of research. It relates to a wide variety of computer science research:

• natural language understanding;
• parallel computing algorithms;
• user interface design and evaluation;
• graph theory; and
• software engineering.

E. Java's Garbage Collection Mechanism

Garbage Collection

Another application of graphs and graph traversals is Java's garbage collection.

Suppose you create an object and then essentially throw it away, e.g.

TreeNode t = new TreeNode("xyz");
    ...
t = null;  // the "xyz" tree node is no longer accessible

You may have done this by accident in work earlier this semester. Sometimes, you may do it intentionally if you know you won't need the object anymore. One might wonder what happens to all these inaccessible objects; do they just hang around, continuing to clutter the program's memory, and if so, doesn't that cause any problems?

The answers are, yes, letting orphaned objects hang around can cause problems (these "memory leaks" can cause a program to run out of memory and crash), but there are remedies. One technique is garbage collection. When available memory for building objects runs out, the system steps in to classify all the program's memory as "in use" or "not in use". It then collects all the "not in use" memory—the "garbage"—in one place, thereby making it available for further uses of new. Garbage collection happens automatically. A Java programmer typically does not have to worry about it.

Language environments that use garbage collection include Java, Python and Scheme. Languages like C and C++ do not. With them, the user must manage his or her own storage; doing this incorrectly is the cause of many frustrating errors in C and C++ programs.

The Garbage Collection Algorithm

In garbage collection, the goal is to find objects that have no references that point to them. Doing this is going to involve graph traversal. What graph are we using? The graph of objects and references: essentially the box and pointer diagrams that you've been drawing all throughout the class!

The garbage collection algorithm requires that each object have a "mark" bit. The algorithm then proceeds like so:

1. First, all the marked bits are turned off. This involves a simple sweep through memory (not a graph traversal); each object has a header that includes its length, so we can just hop from object to object (this includes the orphaned objects).
2. We then mark all the objects that are currently in use. How do we find them? By starting with the references on the system stack (i.e. the local reference variables), going to the objects that those reference, and so on (this part is a graph traversal -- every object is a vertex, and every reference is an edge).

For example, let's work with the Line class that consists of an array of two Points, something that we've worked with early in the semester. In the main method, we may say

Line myLine = new Line(new Point(1,2), new Point(2,2));

The marking process would start by marking the Line object, then the array object that is an instance variable in the Line class, then the two Point references in that array, and finally the Point objects themselves.

1. Finally, the marked memory is compacted, leaving the unused memory all together and ready to be reused. (The bookkeeping necessary to keep references organized as they are moved elsewhere in memory is a bit tricky; you'll study this in CS 61C.)

A Problem with the Marking Phase

All the graph traversals we've done so far have involved an auxiliary structure like a stack or queue to hold the "fringe". When we're doing garbage collection, however, we have run out of memory; setting up a new stack or queue object may not be possible. This seems like a serious problem.

Graph Traversal without a Fringe

A solution to the inability to set up a separate structure to keep track of the traversal is to use the pointer fields in the objects being traversed to store the information that would have gone into the stack. We of course have to restore this information when we're done.

Here's how this technique would work with a linked list. Our task is to go down to the end of the list, then to come back up, revisiting the nodes in reverse order. It's easy enough to go down the list with just an auxiliary pointer:

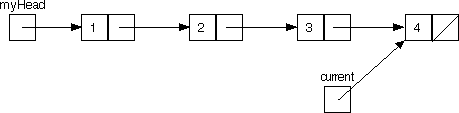
With just this one pointer, once we hit vertex 4 we have no way to go back up to 3 (remember that occasionally in graph traversal we have to backtrack). An idea: add one more auxiliary pointer, and reference the pointers as we go:

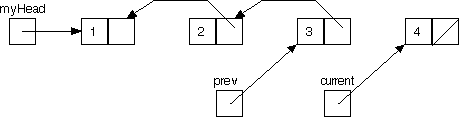
Notice how now once we hit vertex 4, it will be possible to traverse all the way back up to 1.

Reversed Linked List Traversal

Before continuing with the lab, figure out what the statements should be that complete the next step of the backward traversal, that is, the statements that take us from

to

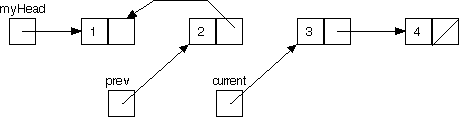
If you're unsure, check your answer with a neighboring partnership.

Tree Traversal without a Stack

Let's expand the idea of reversed linked list traversal without a stack to tree traversal without a stack.

We now present an algorithm by Deutsch, Schorr, and Waite that traverses a binary tree without a stack, using only a constant amount of space plus a "tag" bit and a back-pointer bit in each node. Two pointers are maintained, one named current and the other prev. Going down the tree, current leads the way; prev points to the parent. Going back up the tree, prev leads the way. The left and right pointers keep track of where we've been, and the back-pointer bit indicates which field in the node contains the back pointer. Here are the possibilities.

Notation

What happens when we traverse down the left one step:

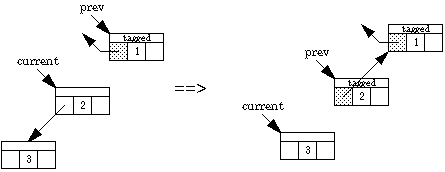
What happens when we traverse down the right one step (if, say, the left is blocked):

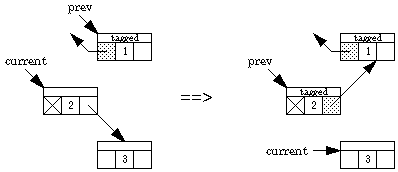
Switching from a left branch to a right branch

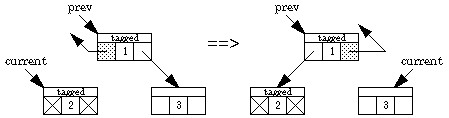
Backing up one step when the back pointer is in the left field

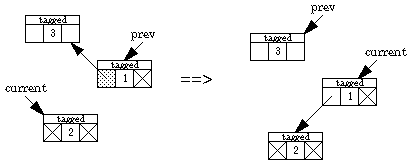
Backing up one step when the back pointer is in the right field

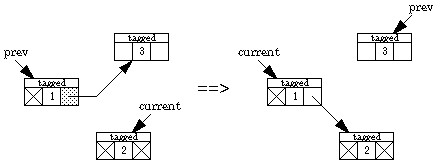
Generalization of Stackless Traversal

We've now seen this pointer-reversal idea used for singly linked lists and binary trees (and graphs with out-degree 2). It can be generalized to more than two outgoing pointers per object; each outgoing pointer is reversed to temporarily hold an incoming pointer.

Thus the garbage collection system is using the programmer's own data structures. Garbage collection must leave them in the same form as they started; the "going back up" process does this.

Cool, right?

Modern Garbage Collection Techniques

In practice, most programs contain a small number of objects that live for a long time, and a large number of objects that come and go quickly. A technique called generational garbage collection handles this by segregating objects that have been around a long time into their own section of memory. These sections of older "generations" get traversed less frequently.

The various steps of garbage collection all basically take over the processing while they do their work. Some real-time applications, however, can't afford to be interrupted by a process as complicated as garbage collection. Modern operating systems allow concurrent garbage collection, where the garbage collector is allowed to run for a short while, then the application program (even though the garbage collection process hasn't finished!), switching back and forth between the two.

F. Getting Started: Autocomplete

At this point, if you haven't already, I recommend you read the (relatively brief) sections of the Project 3 spec on tries and testing. Before leaving lab, write a few unit tests for your as-of-yet unwritten Trie class. You don't need to submit these tests along with today's lab, but these tests will be graded when you turn them in with the remainder of your proj3 work.

G. Conclusion

Submission

As lab20, submit:

• Graph.java, now with Dijkstra's algorithm

Reading

For next lab, please read Jonathan's notes (linked on front page).