A. Intro
Pull the files for lab 23 from the skeleton repository and make a new IntelliJ project out of them.
In previous labs, we have seen various types of graphs, including weighted, undirected graphs, as well as algorithms that can be performed on them. In this lab, we will be introducing Kruskal's algorithm, which can be used to find a minimum spanning tree. Before we can introduce the algorithm, we must first introduce a new data structure that is used in it, disjoint sets.
B. Disjoint Sets
Suppose we have a collection of items, and we want to be able to determine if any two items are connected transitively. For example, if we have a collection of companies that have gone under mergers or acquisitions, we want to develop a data structure that allows us to determine if any two companies are in the same conglomerate, i.e. Google, Niantic, and Alphabet are in the same conglomerate and are all connected.
The disjoint sets data structure represents a collection of sets that are disjoint, meaning that any item in this data structure is found in no more than one set. We will limit our data structure to two operations, union and find. The union operation will combine two sets into one set. The find operation will take in an item, and tell us which set that item belongs to. With this data structure, we will be able to solve the connected components problem efficiently.
Let's say that we had the following companies.

To start off, each company is in its own set with only itself in it. A call to find(Google) will return Google, and so forth for the remaining companies. If we were to do a call to union(Alphabet, Google), the call to find(Google) will now return Alphabet (showing that Google is a part of Alphabet). The unioned result is shown below.

Quick Find
For the rest of the lab, we will work with non-negative integers as the items in our disjoint sets.
One implementation you could think of is that we have each set maintain a list of the items in the set, and each item of the set holds a reference to the set that contains it.
Considering this data structure, how long would the find operation take in the worst case?
|
$\Theta(1)$
|
Correct! Because each item contains a reference to the set it is contained in, we can find in constant time.
|
|
|
$\Theta(\lg n)$
|
Incorrect.
|
|
|
$\Theta(n)$
|
Incorrect.
|
|
|
$\Theta(n \lg n)$
|
Incorrect.
|
|
|
$\Theta(n^2)$
|
Incorrect.
|
How about the worst case runtime of the union operation?
|
$\Theta(1)$
|
Incorrect. Think about all of the other items in the set.
|
|
|
$\Theta(\lg n)$
|
Incorrect.
|
|
|
$\Theta(n)$
|
Correct! Because of we want transitive connectiveness, we must update all of the other items in the set, not just the item we pass into the
union
operation.
|
|
|
$\Theta(n \lg n)$
|
Incorrect.
|
|
|
$\Theta(n^2)$
|
Incorrect.
|
This list-based approach uses the quick-find algorithm, prioritizing the runtime of the find operation. However, union operations are slow.
Quick Union
Suppose we prioritize making the union operation fast instead. One way we can do that is that instead of representing each set as a list, we represent each set as a tree. This tree will be very simple: each node only needs a reference to its parent, and the root of each tree will be the face of the set it represents. In the previous example, Alphabet would be the face of the set represented by Alphabet and Google.
Now union(u, v) is a fast $\Theta(1)$ operation if u and v are both the roots of their own tree, we simply need to make the root of one set connect to the root of another set. The cost of a quick union, however, is that find can now be slow. In order to find which set an item is in, we must travel to the root of the tree, which is $\Theta(N)$ in the worst case (an example of this kind of tree is pictured below). Unioning two leaves could lead to the same case, making union a linear time operation in the worst case. However, we will soon see some optimizations that we can do in order to make this runtime faster.
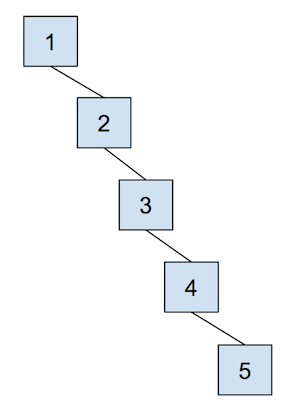
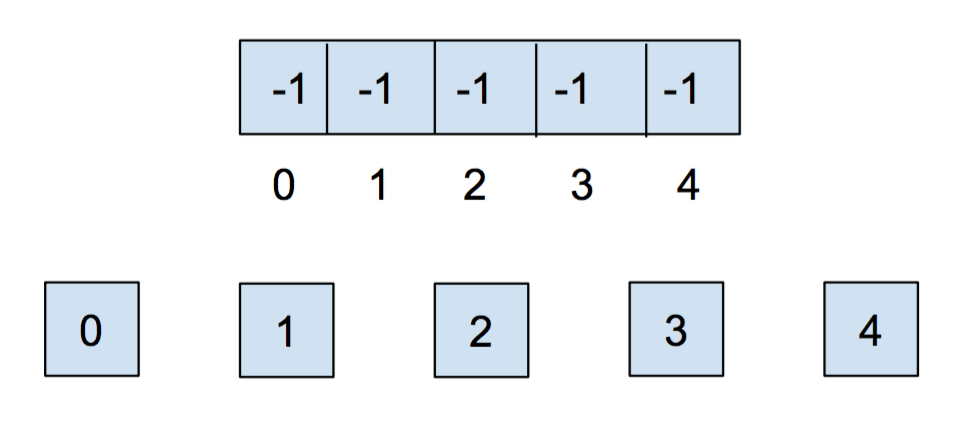
How do we actually create this data structure though? Let's take advantage of the fact that all of our items are non-negative integers. We can then use an array to keep track of our sets. The indices of the array will correspond to the item itself. We will put the parent references inside the array. If an item does not have a parent, we will instead record the size of the set. In order to distinguish that from parent references, we will record the size $s$ of a set, as $-s$ inside of our array.
Because we are using an array as our underlying representation, we must initialize our disjoint sets with a fixed number of sets. Initially, each item is in its own set, so we will initialize all of the elements in the array to -1.
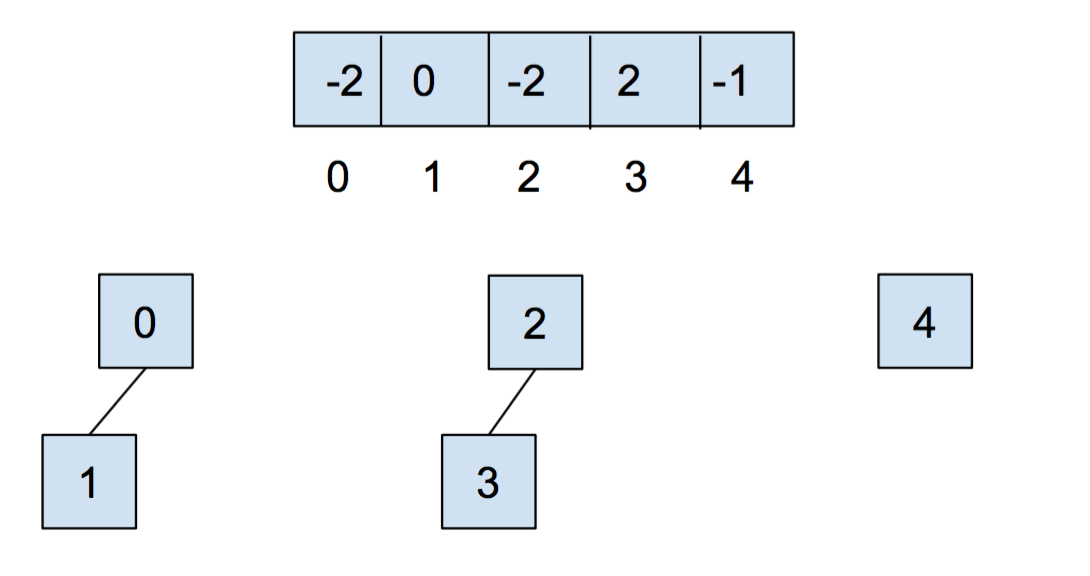
After we call union(0,1) and union(2,3), our array and our abstract representation look as below:
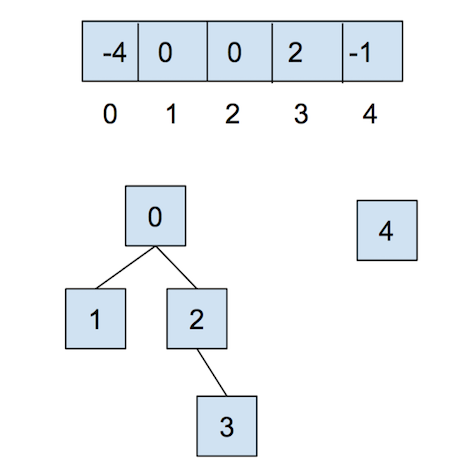
After calling union(0,2), they look like:
Weighted Quick Union
The first optimization that we will do is called "union by size". We do this in order to keep trees as shallow as possible. When we union two trees, we will make the smaller tree a subtree of the larger one, breaking ties arbitrarily. We call this weighted quick union.
Because we are now using "union by size", the maximum depth of any item will be in $O(\lg n)$, where $n$ is the number of items stored in the data structure. Some brief intuition for this is because the depth of any element $x$ only increases when the tree $T_1$ that contains $x$ is placed below another tree $T_2$. When that happens, the size of the resulting tree will be at least double the size of $T_1$ because size($T_2) \ge$ size($T_1$). The tree that contains $x$ can only double its size at most $\lg n$ times until we have reached a total of $n$ items.
Path Compression
Even though we have made a speedup by using a weighted quick union data structure, there is still yet another optimization that we can do. What would happen if we had a tall tree and called find() repeatedly on the deepest leaf? Each time, we would have to traverse the tree from the leaf to the root. A clever optimization is to move the leaf up the tree so it becomes a direct child of the root. That way, the next time you call find() on that leaf, it will run much more quickly. An even more clever idea is that we could do the same thing to every node that is on the path from the leaf to the root, connecting each node to the root as we traverse up the tree. Once you find an item, path compression will make finding it in the future faster.
The running time for any combination of $f$ find and $u$ union operations takes $\Theta(u + f \alpha(f+u,u))$ time, where $\alpha$ is an extremely slowly-growing function called the inverse Ackermann function. And by "extremely slowly-growing", we mean it grows so slowly that for any practical input that you will ever use, the inverse Ackermann function will never be larger than 4 (though it can grow arbitrarily large). That means for any practical purpose (but not on any exam), a quick-union disjoint sets data structure with path compression has find operations that take constant time on average.
You can visit this link here to play around with disjoint sets.
C. Kruskal's Algorithm
Recall that we began the disjoint sets section by mentioning the connected components problem. We'll now see how the disjoint sets can be actually used to solve the transitive connectivity problem and an application where that is needed, Kruskal's Algorithm.
Minimum Spanning Trees
Consider an undirected graph G = (V,E). A spanning tree T = (V, F) of G is tree (which if you recall, is a type of graph) that contains all of the vertices of G and |V| - 1 edges from G. Recall that in a tree, there is only one path between any two vertices. It is possible for G to have multiple spanning trees. Some spanning trees are shown below for a graph G.
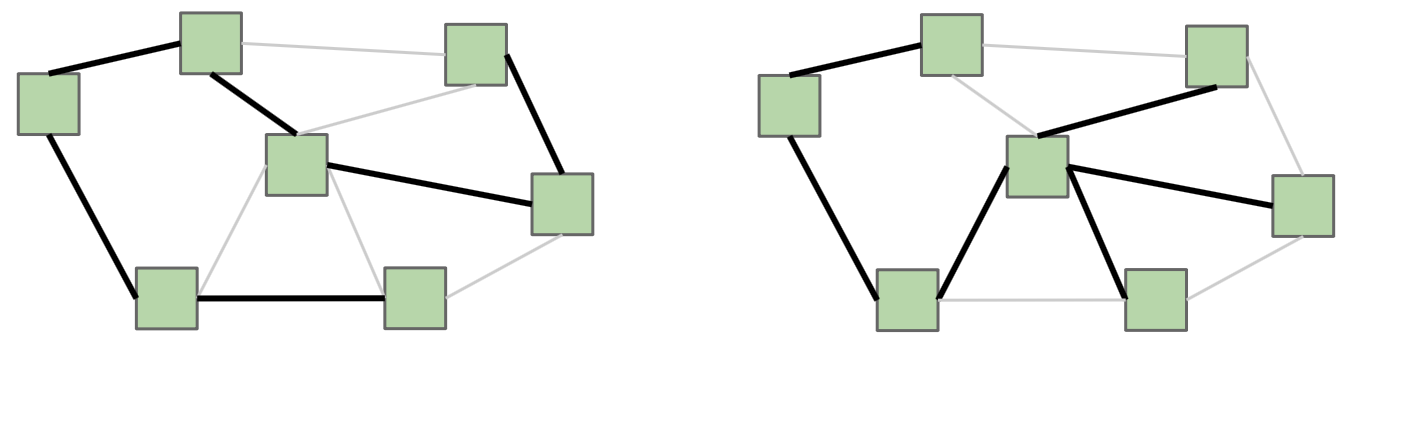
If G is not a connected graph, then a similar idea is one of a spanning forest, which is a collection of trees, each having a connected component of G.
A minimum spanning tree (MST for short) T of a weighted undirected graph G is a spanning tree where the total weight (the sum of all of the weights of the edges) is minimal. That is, no other spanning tree of G has a smaller total weight.
Consider the graph below. Which edge is NOT in the MST of this graph?
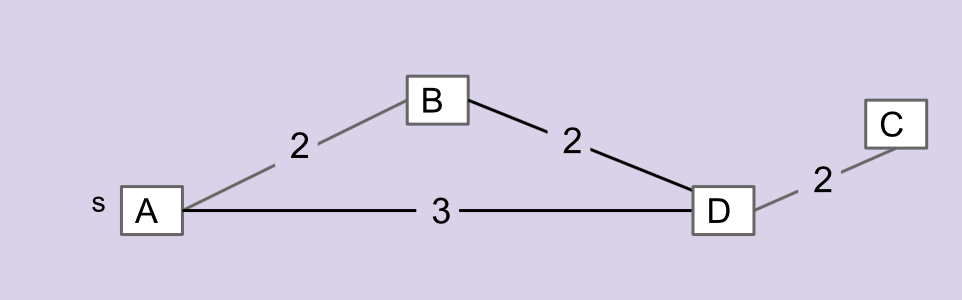
|
AB
|
Incorrect.
|
|
|
AD
|
Correct!
|
|
|
BD
|
Incorrect.
|
|
|
DC
|
Incorrect.
|
Algorithm
Kruskal's algorithm is a type of greedy algorithm (which you will learn more about in CS170) that can calculate the MST of G. It goes as follows:
1. Create a new graph T with the same vertices as G, but no edges (yet).
2. Make a list of all the edges in G.
3. Sort the edges by weight, from least to greatest.
4. Iterate through the edges in sorted order.
For each edge (u, w):
If u and w are not connected by a path in T, add (u, w) to T.Because Kruskal's algorithm never adds an edge if there is a path that already connects it, T is going to be a tree (if G is connected).
As for why Kruskal's algorithm produces a minimum spanning tree, suppose we are considering an edge (u,w) to add to T, and u and w are not yet connected. Let U be all of the vertices in T that have been connected so far to u (by Kruskal's algorithm) and W be a set of vertices of that contains everything else. This partitioning of vertices is called a cut of graph G. Let's define a bridge edge or a crossing edge to be any edge that connects a vertex in U to a vertex in W. A spanning tree of G must contain at least one of these crossing edges to be connected. If we choose the crossing edge with the minimum weight, we know that edge is in the MST. Because we must pick one edge of all these crossing edges to connect U to W, picking the crossing edge with minimum weight will be guaranteed to be in our MST. If there is more than one edge with minimum weight, we can arbitrarily pick one. This is called the cut property.
Because we go through the edges in sorted order by weight and the partitions of vertices U and W have not been connected yet, the edge (u,w) we are considering must be the minimum weight edge across the cut. If (u, w) was not the minimum weight edge across the cut, the partitions would have been connected already by another edge due to the order we iterate through the edges.
How about the runtime of Kruskal's algorithm? As we've seen in previous labs, sorting |E| edges will take $O(|E| \lg |E|)$ time. The tricky part of Kruskal's is determining if u and w are already connected. We could do a DFS or BFS starting from u and seeing if we visit w. However, if we were to do that, Kruskal's would run in worst case $\Theta(|E| |V|)$ time.
However, we just introduced a data structure that can find connections in almost constant time, the disjoint sets data structure. We can have the vertices of G be the items in our data structure. Whenever we add an edge (u,w) to T, we can union the sets that u and w belong in. To check if there is already a path connecting u and w, we can call find() on both of them and see if they are part of the same set. Thus the runtime of Kruskal's is in $O(|E| \lg |E|)$. Note this assumes that graph creation is in constant time. If it is not, then we must take that into consideration as well.
Go here to play around with Kruskal's algorithm.
D. Implementation
For this lab, you will be implementing a naive version of Kruskal's algorithm as well as an optimized version using the disjoint sets data structure. You will be able to time your code using our harness in order to visually confirm that by using clever data structures, you can have remarkable increases in speed!
Graph.java + Edge.java
Graph.java and Edge.java will define the Graph API we will use for this lab. It's a bit different from previous labs and so we will spend a little time discussing its implementation. In this lab, our graph will employ vertices represented by integers, and edges represented as an instance of Edge.java. Vertices are numbered starting from 0, so a Graph instance with n vertices will have vertices numbered from 0 to n-1. A Graph instance maintains three instance variables:
neighbors: a HashMap mapping vertices to a set of its neighboring vertices.edges: a HashMap mapping vertices to its adjacent edges.allEdges: a TreeSet of all the edges present in the current graph.
A Graph instance also has a number of instance methods that may prove useful. Read the documentation to get a better understanding of what each does!
UnionFind.java
When you open up UnionFind.java, you will see that it has a number of method headers with empty implementations. This file will hold your implementation of the disjoint sets data structure. Read the documentation to get an understanding of what methods need to be filled out! Take note of the tie-breaking scheme described in some of the methods and remember to implement both optimizations discussed above. Note that this tie-breaking scheme is chosen arbitrarily. In addition, remember to ensure that the inputs to your functions are valid.
Kruskal.java
Like UnionFind.java, Kruskal.java will also only have method headers initially. This file will hold your implementation of Kruskal's algorithm for calculating MSTs. For this file, you will need to implement isConnected(Graph g, int v1, int v2) which will determine if two vertices are connected using a naive algorithm such as BFS or DFS, minSpanTree(Graph g) which will hold Kruskal's algorithm using the naive implementation of isConnected, and minSpanTreeFast(Graph g) which will hold Kruskal's algorithm using the disjoint sets data structure to efficiently determine if two vertices are connected.
Main.java
This file holds our timing harness. The harness randomly generates a graph and then runs both naive Kruskal's and optimized Kruskal's on it to calculate its MST. It will then print out the time to the command line. By default, Main.java will randomly generate a graph with 1000 vertices, however you can define how many vertices are in the graph by passing in an integer to Main.
>> javac Main.java
>> java Main.java 1337Try running Main.java with commands growing by factors of 10 (100, 1000, 1000). What can you infer about the time as you scale the input size?
Your Task
Your task for this lab is to fully implement the methods in UnionFind.java and Kruskal.java - thus allowing Main.java to function properly. Afterwards, try running Main.java at powers of 10 to see if you see any general patterns about scale. You won't need to turn in your thoughts, but it's a good exercise to solidify your understanding of Kruskal's runtime!
Testing
You'll notice that the code directory has included with it a directory named inputs. This folder contains text documents which can be read in by Graph.java to create a new graph. The syntax is as follows.
# Each line defines a new line in in the graph. The format for each line is
# fromVertex, toVertex, weight
0, 1, 3
1, 2, 2
0, 2, 1This document creates defines a graph with three edges. One from vertex 0 to 1 with weight 3, one from 1 to 2 with weight 2, and one from 0 to 2 with weight 1. You may optionally have your text file only add vertices into the graph. This can be done by having each line contain one number representing the vertex you want to add.
# Start of the file.
0
4
2This creates the graph with vertices 0, 4, and 2. You can define and use your own test inputs by creating a file, placing it into inputs and then reading it in using Graph.loadFromText!
E. Conclusion
Summary
Today we learned about disjoint sets and MSTs. There are other applications that disjoint sets are used for (including maze generation if you want to try it). MSTs also have many usages in the real world, including connections to how the internet works.
Although we restricted ourselves to have disjoint sets with only non-negative integers as its items, we can always create an additional array that maps the integer to an object that we actually want to be in the disjoint sets. However, for many applications, we don't care about that at all, and we care just about the ability to see if two items are in the same set.
There are also other algorithms that you can use to compute the MST, such as Prim's algorithm, which is very similar to Dijkstra's.
Submission
Complete the implementations of UnionFind.java and Kruskal.java. Then, push all files to GitHub.