Navigation
- A. Introduction & Setup
- B. The Trie
- C. AlphabetSort
- D. Autocomplete
- E. Testing
- F. Submission
- G. Acknowledgments
A. Introduction & Setup
In this final project, you will be exploring various applications of Tries. You will be working with your lab partner.
Pull the project skeleton from GitHub:
git pull skeleton masterB. The Trie
Implementation
In Trie.java, implement a Trie as we will cover in lecture in any way you wish. It must implement the following two methods:
public boolean find(String s, boolean isFullWord) {
}
public void insert(String s) {
}And it must support Strings consisting of any sequence of char.
Given some word s of length N, insert should add s to the Trie in O(N) time and space. Note that, for comparison, adding all prefixes of a String of length N to a hash table takes expected O(N^2) time and space.
Given some query String s of length N, find whether or not the query String is in the Trie in O(N) time. If isFullWord is false, then partial prefix matches should return true; if isFullWord is true, then only full word matches should return true.
For example, given the following main method:
public static void main(String[] args) {
Trie t = new Trie();
t.insert("hello");
t.insert("hey");
t.insert("goodbye");
System.out.println(t.find("hell", false));
System.out.println(t.find("hello", true));
System.out.println(t.find("good", false));
System.out.println(t.find("bye", false));
System.out.println(t.find("heyy", false));
System.out.println(t.find("hell", true));
}We should expect to see this as output when the program is run:
true
true
true
false
false
falseError Cases
In your Trie class, throw an IllegalArgumentException when:
- A null or empty string is added. Null and empty strings by definition are never in the Trie.
C. AlphabetSort
As an example use of Tries, consider the following problem:
You are constructing a large dictionary for another language that uses some non-English alphabet. You want this dictionary to be ordered in the same way the foreign alphabet is ordered. This dictionary is very large, and you don't want to use a O(NM log N) time comparison-based sorting algorithm (where N is the number of words and M is the max length of the words).
AlphabetSort sorts a list of words into alphabetical order, according to a given permutation of some alphabet. It takes input from stdin and prints to stdout. The first line of input is some alphabet permutation. The remaining lines are the words to be sorted. The output should be the sorted words, each on its own line, printed to stdout. The runtime should be linear in the length of the file: if the longest word is of length M and we have N words then it should run in time O(MN).
For example: given some input file called test.in with the following content:
agdbecfhijklmnopqrsty
hello
goodbye
goodday
deathWe should expect to see this as output when the program is run with test.in.
To use test.in as the input file, we use input redirection, linking stdin to a file descriptor:
$ java AlphabetSort < test.inExpected output:
goodday
goodbye
death
helloNOTE: "goodday" is before "goodbye" because in the specified ordering of the alphabet, "d" comes before "b". Both "goodday" and "goodbye" are before "death" and "hello" because "g" comes before either "d" or "h" in the specified ordering of the alphabet.
Warning: Do not use the StdIn class from the Princeton Standard Library. It's buggy and you might fail the autograder.
Special Cases
In your AlphabetSort class, throw an IllegalArgumentException when:
- No words or alphabet are given.
- A letter appears multiple times in the alphabet.
In addition, if an input word has a character that is not in the alphabet, ignore that word.
D. Autocomplete
Description
Autocompletion is an extremely common feature amongst software. Use cases range from web search to text editors; as a result, string algorithms are fairly well studied.
In this part, you will implement an immutable data type that provides autocomplete functionality for a given set of terms and weights. You will implement the following API:
public class Autocomplete {
/**
* Initializes required data structures from parallel arrays.
* @param terms Array of terms.
* @param weights Array of weights.
*/
public Autocomplete(String[] terms, double[] weights) {
}
/**
* Find the weight of a given term. If it is not in the dictionary,
* return 0.0.
*/
public double weightOf(String term) {
}
/**
* Return the top match for given prefix, or null if there is no
* matching term.
* @param prefix Input prefix to match against.
* @return Best (highest weight) matching string in the dictionary.
*/
public String topMatch(String prefix) {
}
/**
* Returns the top k matching terms (in descending order of weight)
* as an iterable.
* If there are less than k matches, return all the matching terms.
*/
public Iterable<String> topMatches(String prefix, int k) {
}
}Your algorithm should have a best case runtime that is much less than the number of matching prefixes.
Put more formally, let Np be the number of terms that match a query prefix p. For a best case input, your program should consider fewer than Np weights when collecting the top k matches. What constitutes a best case input depends on your implementation. Put another way, your algorithm should not have the property that it always examines all Np prefix matches.
Basically what this means is that your code shouldn't be checking every possible match for some prefix. You will be graded on runtime.
Your constructor should run in O(nm) time where n is the number of terms and m is the max length of the input terms.
It is up to you to decide which data structures and algorithms to design and use. The final subsection describes one sample effective strategy. You don't have to use it if you think your design will also meet the runtime requirements.
There is one caveat though: any data structures or libraries you use must come from the Java Standard Library; if it does not have something you need, write your own.
Input format
We provide a number of sample input files for testing. Each file consists of an integer N followed by N pairs of terms and positive weights. There is one pair per line, with the weight and term separated by a tab. The terms can be arbitrary strings consisting of Unicode characters, including spaces (but not tabs or new lines).
The file wikitionary.txt contains the 10,000 most common words in Project Gutenberg along with weights equal to their frequencies. The file cities.txt contains nearly 100,000 cities along with weights equal to their populations.
Input parsing is given to you in the form of a command-line test client in the skeleton code.
Your task
Implement Autocomplete.java to conform to the above runtime requirements. The skeleton gives the interface you must implement, along with a test client for your testing convenience.
You may break ties arbitrarily for this and the following part.
Here are a few sample executions of the test client that are also reflected in the autograder:
$ java Autocomplete wiktionary.txt 5
auto
6197.0 automobile
4250.0 automatic
comp
133159.0 company
78039.8 complete
60384.9 companion
52050.3 completely
44817.7 comply
the
56271872.0 the
3340398.0 they
2820265.0 their
2509917.0 them
1961200.0 there
$ java Autocomplete cities.txt 7
M
12691836.0 Mumbai, India
12294193.0 Mexico City, Distrito Federal, Mexico
10444527.0 Manila, Philippines
10381222.0 Moscow, Russia
3730206.0 Melbourne, Victoria, Australia
3268513.0 Montreal, Quebec, Canada
3255944.0 Madrid, Spain
Al M
431052.0 Al Mahallah al Kubra, Egypt
420195.0 Al Mansurah, Egypt
290802.0 Al Mubarraz, Saudi Arabia
258132.0 Al Mukalla, Yemen
227150.0 Al Minya, Egypt
128297.0 Al Manaqil, Sudan
99357.0 Al Matariyah, EgyptError Cases
There are several cases in which you should throw an IllegalArgumentException:
- The length of the terms and weights arrays are different
- There are duplicate input terms
- There are negative weights
- Trying to find the k top matches for non-positive k.
Sample Approach
Here, we will suggest one strategy that combines a Ternary Search Trie with a priority queue. The ternary search trie (TST) contains all of the terms, along with their weights. In addition, each node stores the maximum weight of its subtries - we will exploit this auxiliary information when we implement the search algorithm. You do not have to use this approach. An augmented trie can also work, depending on implementation details.
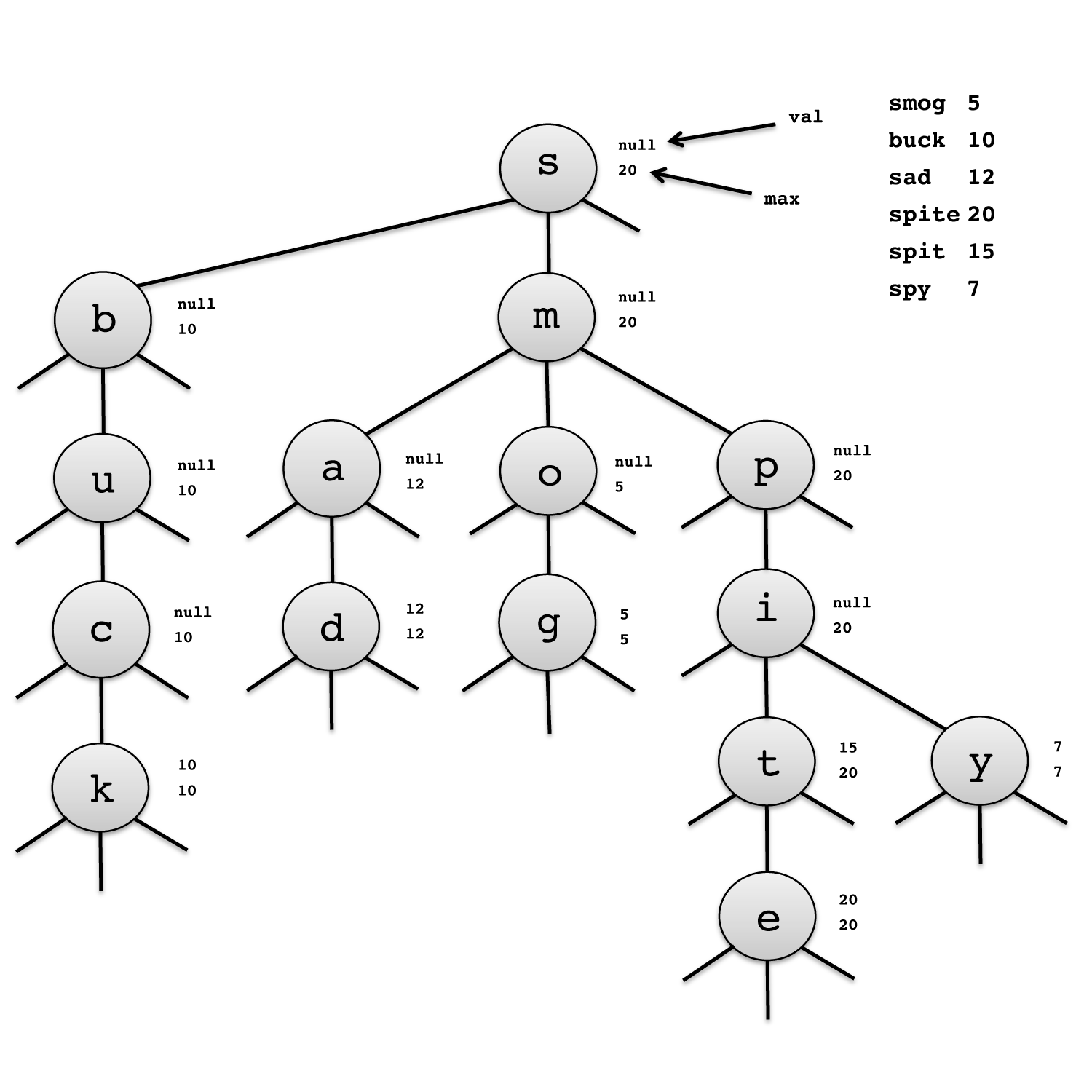
NOTE: A TST does not store words in the same way as a Trie! For example, the word "sbuck" is not in this TST (it's not a word in the first place!).
The TST shown above contains the words "smog", "buck", "sad", "spite", "spit", and "spy". In our implementation, we've essentially "reached" a word when we see that a weight has been set for it (e.g. at "k" on the left bottom node for the word "buck", the weight is set to 10.
If a given prefix matches some node's character, we can descend into that node's middle subtrie. If not, we look either to the left or right subtrie, depending on whether or not the character comes before or after the node. For example, for the word "buck", since "b" doesn't match "s", we look to the left subtrie because "b" < "s" and find "b".
For the word "sad", we first match with "s", then see that "a" < "m", so we descend into the left subtrie of the "m" node.
For our problem, we need to find the top k terms among those that start with a given prefix. All of the matching words are in the subtrie corresponding to the prefix, so the first step is to search for this node, say x. Now, to identify the top k matches, we could examine every node in the subtrie rooted at x, but this takes too long if the subtrie is large. Instead, we will use the weight of the node and the maximum weight of its subtries to avoid exploration of useless parts of the subtrie.
Specifically, we execute a modified tree traversal on the TST where we use a priority queue (instead of a stack for DFS or queue for BFS) pq that is maximally-oriented on the heaviest reachable node and we keep track of a Collection bestAnswer of the k highest weighted prefix-matching terms seen so far.
We can terminate the search as soon as the weight of the heaviest reachable node in the priority queue pq is less than or equal to the weight of the kth heaviest term in the Collection bestAnswer, because no remaining term in the subtrie has weight larger than the weight of the heaviest node in pq.
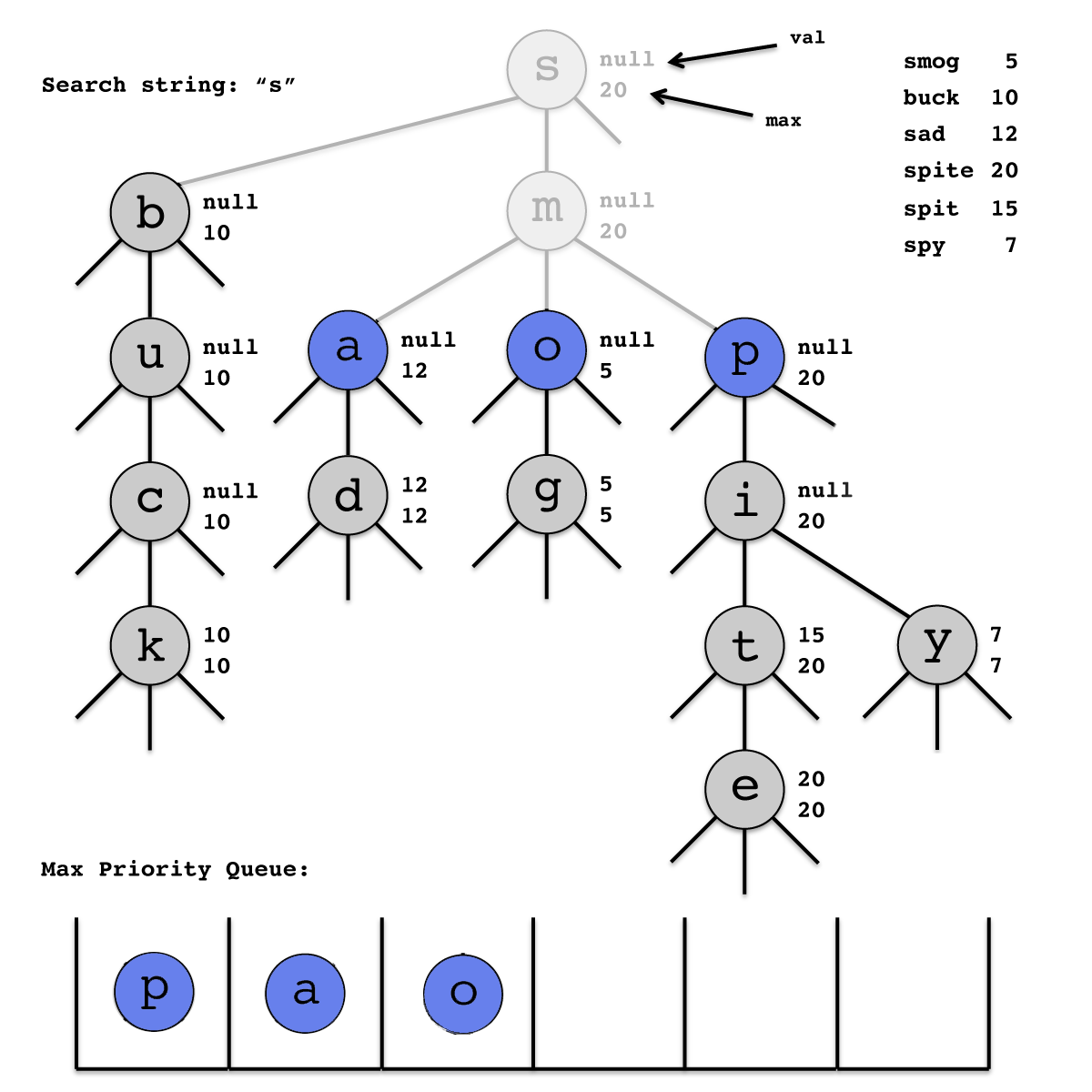
Below is a snapshot of the algorithm when searching for the top 3 terms that start with the prefix "s". The next node to be examined is the one containing the letter "p". The first matching term that is discovered will be "spit", followed by "spite", and "sad". The subtries rooted at "y" and "o" will never be explored.
Interactive GUI
Interactive GUI (optional, but fun and no extra work). Compile AutocompleteGUI.java. The program takes the name of a file and an integer k as command-line arguments and provides a GUI for the user to enter queries. It presents the top k matching terms in real time. When the user selects a term, the GUI opens up the results from a Google search for that term in a browser.
E. Testing
To get full credit on this project, your Trie and Autocomplete classes must be thoroughly unit tested. You must place your tests in the given TestTrie.java and TestAutocomplete.java files and submit them along with the rest of your code. Your tests will be graded manually by the staff and will be worth four points.
F. Submission
Submit the following files, any of their dependencies, and whatever tests you have written:
Trie.javaAlphabetSort.javaAutocomplete.java
by pushing to your group repository.
Please ensure that your code is within the style guidelines, and your methods and classes are well commented, explaining their implementations and runtimes.
G. Submission
This project is borrowed from Josh Hug's spring 2015 offering of CS 61B.