A. Intro
Obtaining the Files
Pull the files for lab 15 from the skeleton.
Learning Goals
In today's lab, we'll learn about an incredible data structure that can provide constant time insertion, removal, and containment checks. Yes, you read that correctly: constant, $O(1)$, runtime! In the best case scenario, the hash table can provide amortized constant time access to its elements regardless of whether we're working with 10 elements, 1,000 elements, or 1,000,000 elements.
Before we jump in to hash tables, we'll first introduce a small example class, SimpleNameMap, that provides a mapping from first names to last names and implements some of the basic ideas behind hashing. Through the course of this lab, we will add new functionality for the SimpleNameMap to make it more robust. We will also analyze the SimpleNameMap to see exactly how it works and why we need to make a distinction between the best and worst case runtimes.
Finally, we'll implement a real HashMap by generalizing the lessons we learned in the process of developing SimpleNameMap. Along the way, we'll also discuss the merits and drawbacks of Java's hashCode, or hash function, and how we can design our own hash functions.
B. Fast Maps
TreeMap
Recall that we developed a binary tree-based Set implementation last lab. It was certainly quite fast with $O(\log N)$ insertion, retrieval, and removal assuming a balanced tree. But I think we can do even better!
Discussion: Faster Than Fast
How can we design a constant time implementation of Map? If you're familiar with Python, a map is like a dictionary: it provides a mapping from some key (like a word in an English dictionary) to its value (like the definition for that word). It's similar to Set in that keys are guaranteed to be unique.
We need to design a data structure where, no matter how many elements we insert into the Map, we can still retrieve any single element in $O(1)$ time. Remember that a balanced TreeMap can take up to $O(\log N)$ time to retrieve any single element because we may need to traverse $\log N$ other nodes to reach a leaf at the bottom of the tree. Our goal, then, is to figure out how we can design a Map that does not need to consider any significant portion of other keys.
Hint: Which data structure have we seen before in class that provides constant-time access to any arbitrary element? What kind of changes might we need to implement to make it work with the Map interface?
C. SimpleNameMap
A Constant Time Implementation
We've seen before in class that arrays are fast. Unlike a linked list or a tree, there’s no need to traverse any part of the collection to reach an element: we can simply use bracket notation, array[i], to jump right to the ith index in constant time.
For the most part, this works great! Consider the following implementation of a simple Map that associates a number with each key. In this scheme, we let the first letter in each key name determine its index in the final array. For example, if the key is "Aidan", the letter 'A' tells us that this key-value pair will map to array[0].
| Key | Value | Array Index |
|---|---|---|
| "Aidan" | "Clark" | 0 |
| "Brijen" | "Thananjeyan" | 1 |
| "Daniel" | "Nguyen" | 3 |
| "Giulio" | "Zhou" | 6 |
| "Kevin" | "Lin" | 10 |
| "Matt" | "Mussomele" | 12 |
| "Sarah" | "Kim" | 18 |
| "Wan Fung" | "Chui" | 22 |
We can define this process in a hash function whose job, when given a key, is to return a specific integer for that key. In this case, the hash function uses the first character of the string to figure out the correct index to return.
public class String {
public int hashCode() {
return (int) (this.charAt(0) - 'A');
}
}(We want to subtract 'A' because the ASCII table encodes the capital letter 'A' as starting at 65, not 0.)
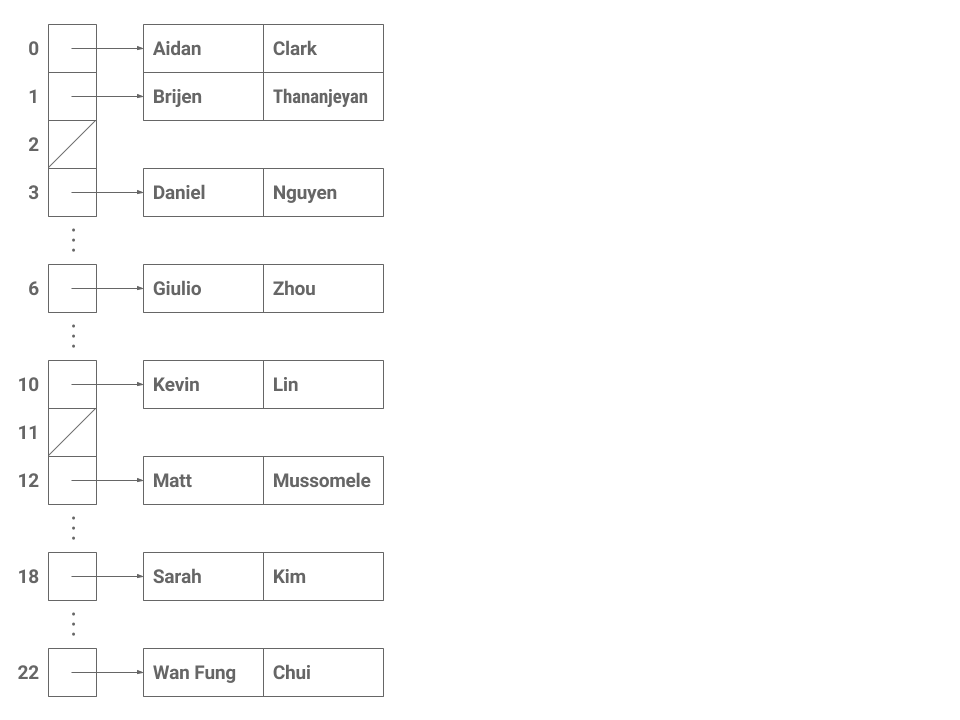
Since we know exactly which index each string will map to, there's no need to iterate across the entire array to find a single element! For example, if we put "Giulio" into the map, we can find it later by simply indexing to array[6] because Giulio's 'G' lives in the sixth array entry. Insertion, removal, and retrieval of a single element in the table, no matter how full, will only ever take constant time because we can just index based on the first character of the key's name.
Exercise: Introduction to SimpleNameMap
Take a look around SimpleNameMap.java. We've started you off with a very basic skeleton containing a simple Entry static nested class which is used to represent an entry, or key-value pair, in our map. There's also a helper function isValidName(String key) which tells us if a given key is a valid name starting with an uppercase letter.
Implement an array-backed data structure based on the details above in SimpleNameMap.java. Fill in a constructor, add any instance variables if necessary, and implement the following methods.
/** Returns true if the map contains the KEY. */
boolean containsKey(String key);
/** Returns the value for the specified KEY. */
String get(String key);
/** Put a (KEY, VALUE) pair into this map. */
void put(String key, String value);
/** Remove a single entry, KEY, from this table and return the VALUE if successful or NULL otherwise. */
String remove(String key);You may also want to write your own hash(String key) function that works like the String.hashCode() example introduced above to simplify the code. Remember that we need to subtract 'A' when hashing so that the zero-indexing will work correctly!
Limitations
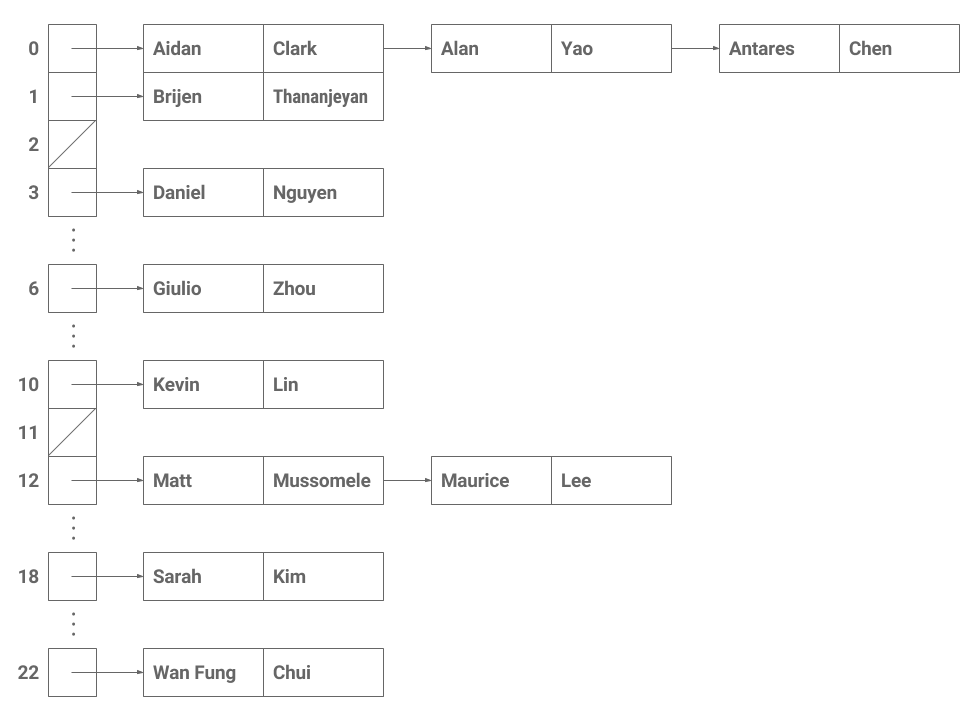
Now that we've completed a basic implementation of SimpleNameMap, can you spot any problems with the design? Consider what happens if we try to add all the TA's to the map like below.
| Key | Value | Array Index |
|---|---|---|
| "Aidan" | "Clark" | 0 |
| "Alan" | "Yao" | 0 |
| "Antares" | "Chen" | 0 |
| "Brijen" | "Thananjeyan" | 1 |
| "Daniel" | "Nguyen" | 3 |
| "Giulio" | "Zhou" | 6 |
| "Kevin" | "Lin" | 10 |
| "Matt" | "Mussomele" | 12 |
| "Maurice" | "Lee" | 12 |
| "Sarah" | "Kim" | 18 |
| "Wan Fung" | "Chui" | 22 |
Discussion: Not Quite Perfect
What are the drawbacks of the SimpleNameMap?
If we simply try to add all the elements in the table above to the map, what will happen?
What if we want to use lowercase letters or special characters as the first letter of the name? Or any character, ever, in any language?
How can we use this structure with objects other than strings?
- Collisions: Aidan, Alan, and Antares all share index 0 while Matt and Maurice both share index 12. What happens if we need to include multiple A-names or M-names in our
SimpleNameMap? - Memory inefficiency: The size of our array needs to grow with the size of the alphabet. For English, it's convenient that we can just use the first letter of each name. But in other languages, that might not be true. And to support any possible symbol, we might need an array with a length in the thousands or millions to ensure complete compatibility even though we may only need to store a handful of names.
- Hashing: How do we generalize the indexing strategy in
SimpleNameMap? The underlying principle behind hashing is that it provides a scheme for mapping an arbitrary object to an integer. For string names, we can get away with using the first character, but what about other objects? How can we reliably hash an object like aPotato?
We'll see later that all three of these points above play a large role in the runtime and efficiency of a hash table. For the remainder of this lab, we will be extending the SimpleNameMap to workaround each of these limitations before implementing a fully-fledged HashMap that implements Map61BL.
D. The Hash Table
Collisions
In the previous example, the keys had mostly different values, but there were still several collisions caused by distinct keys sharing the same hash value. "Aidan", "Alan", and "Antares" are all distinct keys but they happen to map to the same array index, 0, just as "Matt" and "Maurice" share the index 12. Other hash functions, like one depending on the length of the first name, could produce even more collisions depending on the particular data set.
There are two common methods of dealing with collisions:
- Linear Probing: Store the colliding keys elsewhere in the array, potentially in the next open array space. Rarely used in practice.
- External Chaining: A simpler solution is to store all the keys with the same hash value together in a collection of their own, such as a linked list. This collection of entries sharing a single index is called a bucket.
We primarily discuss external chaining implemented using linked lists in this course. Here are the example entries from the previous step, hashed into a 26-element table of linked lists using the function based on the first letter of the string as defined earlier.
public class String {
public int hashCode() {
return (int) (this.charAt(0) - 'A');
}
}
Inserting ("Alan", "Yao") into this map after previously inserting ("Aidan", "Clark") appends Alan's entry to the end of the linked list.
Discussion: External Chaining
What happens if we were to insert the following sequence of key-value entries? Describe the step-by-step process in as much detail as you can.
("Aidan", "Clark"), ("Sarah", "Kim"), ("Alan", "Yao"), ("Antares", "Chen"), ("Alan", "Yao")Now, a bit of runtime analysis! Assume for a moment that all of the keys in the table have different hash codes and, as a result, end up in different indices in the array. What is the runtime of getting a key with respect to the total number of keys, $N$, in the map?
An example input might look like: ("Brijen", "Thananjeyan"), ("Sarah", "Kim"), ("Maurice", "Lee").
$O(1)$. We can index into the array in constant time. Then we search for the key in the bucket. But there is only one item in the bucket, so this search also runs in $O(1)$ time.
Now, assume instead that all the keys in the table happen to have the same hash code (despite being different keys), and they end up in the same bucket. For example, suppose all our keys begin with the letter 'A'. If we add external chaining, what is the runtime of getting a key with respect to the total number of keys, $N$, in the map?
An example input might look like: ("Aidan", "Clark"), ("Alan", "Yao"), ("Antares", "Chen").
$O(N)$ in the worst case where $N$ is the number of keys in the map. To find a key, we first index into the array at the proper location in constant time. But then we have to search through all of the items in the bucket to find the appropriate key. If the bucket is a linked list, we just have to iterate through the linked list until we find the key. In the worst case, all the keys end up in the same bucket, so this could take up to $N$ steps.
Exercise: Implementing External Chaining
Let's add external chaining to our SimpleNameMap. We can either use Java's LinkedList class or modify the Entry static nested class (by adding next pointers) to support multiple entries in a bucket.
Make changes to the following functions to support external chaining.
boolean containsKey(String key);
String get(String key);
void put(String key, String value);
String remove(String key);Remember that any class that implements Map cannot contain duplicate keys.
Note that if you're using the Java LinkedList, you'll need to put in a little work to get it working with Java arrays. See this StackOverflow post and this one as well for workarounds.
Reasonably-Sized Tables
Another issue that we discussed is memory inefficiency: for a small range of hash values, we can get away with an array that individuates each hash value. This works well if our indices are small and close to zero. But remember that Java's 32-bit integer type can support numbers anywhere between -2,147,483,648 and 2,147,483,647. Now, most of the time, our data won't use anywhere near that many values. But even if we only wanted to support special characters, our array would still need to be 1,112,064 elements long!
Instead, we'll slightly modify our indexing strategy. Let's say we only want to support an array of length 10 so as to avoid allocating excessive amounts of memory. How can we turn a number that is potentially millions or billions large into a value between 0 and 9, inclusive?
This is exactly how modulus works. Remember that the modulo operator is like a remainder. For example, $65 \equiv 5 \mod 10$ because, after subtracting 60, we're left with a remainder of 5. A number in mod 10 will return an integer value between 0 and 9 which is exactly what we need to index into an array of size 10.
More generally, we can locate the correct index for any key with the following.
key.hashCode() % array.lengthIn Java, the % operator takes the modulus.
Exercise: Adding modulo
Make changes to the following functions to support modulo.
boolean containsKey(String key);
String get(String key);
void put(String key, String value);
String remove(String key);E. Hashing
Hash Functions
The idea underlying hashing is the transformation of any object into a number. If this transformation is fast and different keys transform into different index values, then we can approximate the direct, constant-time access that an array provides.
The transforming function is called a hash function, and the int return value is the hash value. In Java, hash functions are defined in the object's class as a method called hashCode with return value int. The built-in String class, for example, might have the following code.
public class String {
public int hashCode() {
...
}
}This way, we can simply call key.hashCode() to generate an integer hash code for a string instance called key.
Exercise: Using hashCode
Now, modify our SimpleNameMap so that, instead of using the first character as the index, we instead use key's hashCode method.
Make changes to the following functions to support hashCode.
boolean containsKey(String key);
String get(String key);
void put(String key, String value);
String remove(String key);Note that, to use hashCode results as an index, we must convert the hash code to a valid index. Because hashCode can return negative values, use
hashCode() & 0x7FFFFFFFto return only a non-negative index instead.
Runtime Considerations
We learned earlier that collisions are troublesome: exactly how many collisions occur defines the difference between an $O(1)$ runtime or an $O(N)$ runtime. To reduce collisions and distribute entries throughout the table, our hash function should return distinct values for different keys.
Discussion: Collisions
Given the following dataset, compare the first-letter hash function we defined earlier against the results of Java's String.hashCode.
| Key | First | First % 10 | hashCode |
hashCode % 10 |
hashCode % 23 |
|---|---|---|---|---|---|
| "Aidan" | 0 | 0 | 63256137 | 7 | 19 |
| "Alan" | 0 | 0 | 2043320 | 0 | 0 |
| "Antares" | 0 | 0 | 817534694 | 4 | 16 |
| "Brijen" | 1 | 1 | 1998038522 | 2 | 2 |
| "Daniel" | 3 | 3 | 2039744959 | 9 | 10 |
| "Giulio" | 6 | 6 | 2133232127 | 7 | 21 |
| "Kevin" | 10 | 0 | 72389729 | 9 | 12 |
| "Matt" | 12 | 2 | 2390836 | 6 | 9 |
| "Maurice" | 12 | 2 | 359402906 | 6 | 7 |
| "Sarah" | 18 | 8 | 79654635 | 5 | 0 |
| "Wan Fung" | 22 | 2 | 375148228 | 8 | 12 |
Describe the differences. Which hash code, first letter or String.hashCode, minimizes the number of collisions? What else affects the number of collisions?
Load Factor
No matter what, if the underlying array of our hash table is small and we add a lot of keys to it then we will start getting more and more collisions. Because of this, a hash table should expand its underlying array once it starts to fill up (much like how an ArrayList expands once it fills up).
To keep track of how full our hash table is, we define a load factor which is a fraction between 0 and 1 giving the upper limit for the ratio of the number of entries over the total physical length of the array.
$\text{Load factor} = \frac{size()}{\texttt{array.length}}$
Once the number of keys, $size()$, causes the ratio to exceed the specified load factor, then the hash table should resize, usually by doubling the array length. Java's default load factor is 0.75 which provides a good balance between a reasonably-sized array and reducing collisions.
As an example, let's see what happens if our hash table has an array length of 10 and currently contains 7 elements. Each of these 7 elements are hashed modulo 10 because we want to get an index within the range of 0 through 9. The current load factor is $\frac{7}{10}$, or 0.7, just under the threshold.
If we insert one more element, we'll have 8 elements and a load factor of 0.8. This necessitates a resize to an array of size 20. Remember that since our procedure for locating an entry in the hash table is to take the hashCode() % array.length, since our array's length has changed from 10 to 20, all the elements in the hash table need to be relocated.
Exercise: Implementing Resizing
Update SimpleNameMap to include the automatic resizing feature described above. For the purposes of this assignment, just implement resizing upwards from smaller arrays to larger arrays. (In real life, Java's HashMap also resizes downward if enough entries are removed from the map.)
Make changes to the following functions to support resizing.
void put(String key, String value);It might help to write a resize helper method instead of trying to cram all the details into put.
Discussion: Putting It All Together
We've learned that external chaining is one method for resolving collisions in our hash table. But why use a linked list? Why not use an array instead? What are the benefits and drawbacks of each?
How does the load factor play a part in this? Assuming that the keys are perfectly distributed, how many entries should be in each bucket and how does this affect the runtime?
Java hashCode Functions
Print the hash values for several instances of builtin classes such as java.awt.Point, java.lang.String, and java.lang.Integer to get an idea of what kind of values a hashCode method typically produces.
Browse the Java 8 source for Point.hashCode(), String.hashCode(), and Integer.hashCode(). Try to explain to yourself how each hashCode method works.
Discussion: Inventing a Hash Function
Here are eleven integer keys.
10 100 32 45 58 126 1 29 200 400 15Using what we've learned thus far, define a hash function that, when used with an empty chained table of size 11, produces three or fewer total collisions when the eleven keys are added to the table. Jot down your ideas or write a little pseudocode describing your function. Then, discuss your hash function with your neighbors.
F. HashMap
Exercise: Write HashMap
We've covered all the basics in a hash table. Now, let's write HashMap.java! Or, rather, since we've already written SimpleNameMap.java, let's just make the necessary changes to generalize the code to comply with Map61BL.
Copy SimpleNameMap.java to a file named HashMap.java and modify the type parameters everywhere in the code so that the key and value are generic types. For example, the class header might read:
public class HashMap<K,V> implements Map61BL<K,V>Remember also to modify method return values and formal parameters. Don't forget to implement the following additional functions as required by the Map61BL interface!
/** Removes all of the mappings from this map. */
void clear();
/** Returns an Iterator over the keys in this map. */
Iterator<K> iterator();
/** Remove and return a particular key-value mapping. */
V remove(K key, V value);In implementing iterator, you may find it useful to write another inner class. Refer back to the lab on iterators for more ideas. The iterator does not need to implement remove since it's an optional operation, so just throw new UnsupportedOperationException() in that case.
To speed up testing, we've provided the full test suite in the skeleton. Our tests additionally expect a couple of extra constructors and methods:
/** Create a new hash map with a default array of size 16 and load factor of 0.75. */
HashMap();
/** Create a new hash map with an array of size INITIALCAPACITY and default load factor of 0.75. */
HashMap(int initialCapacity);
/** Create a new hash map with INITIALCAPACITY and LOADFACTOR. */
HashMap(int initialCapacity, float loadFactor);
/** Return the capacity of this hash table's internal array. */
int capacity();G. Conclusion
Summary
In this lab, we learned about hashing, a powerful technique for turning a complex object like a String into a smaller, discrete value like a Java int. The hash table is a data structure which combines this hash function with the fact that arrays can be indexed in constant time. Together, under the right circumstances, we can build a HashMap which allows for amortized constant time access to any single element so long as we know which bucket it falls into.
However, we quickly demonstrated that the naive implementation has several drawbacks: collisions, size limitations, and the hash function itself. To workaround each of these challenges, we introduced three different features:
- We added external chaining to solve collisions by allowing multiple entries to live in a single bucket.
- To allow for smaller array sizes, we used the modulo operator to shrink hash values down to within a specified range.
- Lastly, we compared the first-letter hash function to Java's
String.hashCodeto see how different hash functions distributed keys and how it affects the runtime of the hash table.
In the next lab, we'll discuss some of the finer details of hashing.
Submission
Turn in the completed HashMap.java.