Introduction
This initial programming assignment is intended as an extended finger exercise, a mini-project rather than a full-scale programming project. True, there is quite a bit of background reading, but the necessary program is not (or rather need not be) terribly big. The intent is to give you a chance to get familiar with Java and the various tools used in the course.
We will be grading solely on whether you manage to get your
program to work (according to our tests) and to hand in the assigned
pieces. There is a slight stylistic component: the submission and
grading machinery require that your program pass a mechanized style
check (style61b), which mainly checks for formatting and the
presence of comments in the proper places. See the course website for a brief description of the style rules.
To obtain the skeleton files (and set up an initial entry for your project in the repository),
you can use the command git pull skeleton master. From there, you can set up an IntelliJ project as you did in the labs.
Background
You may have heard of the Enigma machines that Germany used during World War II to encrypt its military communications. If you have not, I recommend you read the wikipedia page on them (or whatever resource you wish), especially the part about design and operation. This project involves building a simulator for a very simplified version of this machine (there were actually a number of varieties of the machine, each implementing its own encryption algorithm. Ours is probably closest to M4, used by the German navy. We have left off the plugboard (Steckerbrett,) which added an additional configurable permutation to the encryption, increasing the number of possible configurations by a factor of roughly $5.5\times10^{20}$. We've also omitted the configurability of the alphabet ring (Ringstellung) on each rotor, which allowed changing the points at which the rotor sequenced). Your program will take descriptions of possible initial configurations of the machine and messages to encode or decode (the Enigma algorithms were reciprocal, meaning that the encryption is its own inverse operation.)
The Enigmas effect a substitution cipher, on the letters of a message. That is, at any given time, the machine performs a permutation---a one-to-one mapping---of the alphabet onto itself. The alphabet consists solely of the 26 letters in one case (there were various conventions for spaces and punctuation).
Plain substitution ciphers are easy to break (you've probably seen puzzles in newspapers that consist of breaking such ciphers). The Enigma, however, implements a progressive substitution, different for each subsequent letter of the message. This made decryption considerably more difficult.
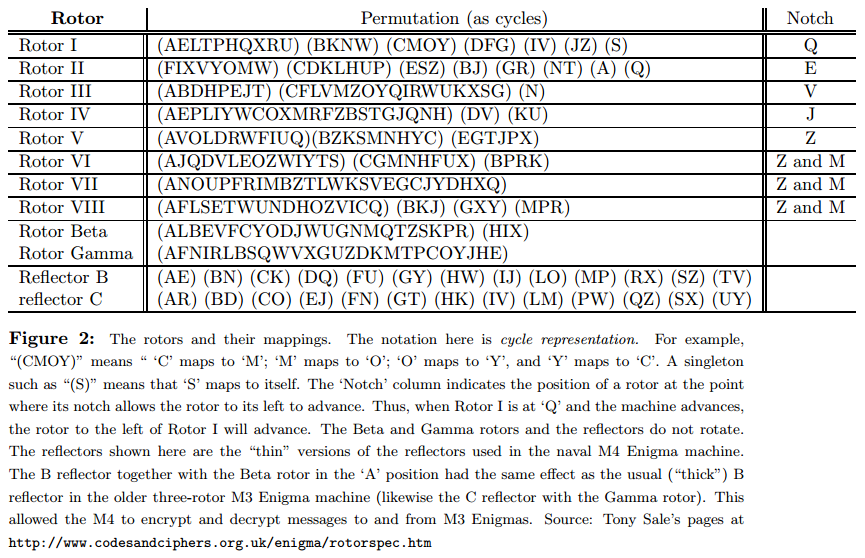
The device consists of a simple mechanical system of interchangeable rotors (Walzen) that sit side-by-side on a shaft and make electrical contact with each other. In our simulator, there will be a total of 12 rotors:
- Eight rotors labeled with roman numerals I—VIII, of which three will be used in any given configuration as the rightmost rotors,
- Two additional non-moving rotors (Zusatzwalzen) labeled "Beta" and "Gamma", of which one will be used in any configuration, as the fourth-from-right rotor, and
- Two special reflectors (Umkehrwalzen), labeled 'B' and 'C', of which one will be used in any given configuration as the leftmost rotor.
Each of the first ten rotors has 26 contacts on both sides, which are wired together internally so as to effect a permutation of signals coming in from one side onto the contacts on the other (and the inverse permutation when going in the reverse direction). The reflectors are special "rotors" that don't rotate during translation and have all of their contacts on one side. They simply connect half of their contacts to the other half. Figure 2 shows the permutations implemented by all the rotors and reflectors.
A signal starting from the right through one of the 26 possible contacts will flow through wires in four rotors, "bounce" off the reflector, and then come back through the same rotors by a different route, always ending up permuted to a letter position different from where it started (A significant crytographic weakness, as it turned out. It doesn't really do a would-be code-breaker any good to know that some letters in an encrypted message it might be the same as the those in the plaintext if he doesn't know which ones. But it does a great deal of good to be able to eliminate a possible decryption because one position in the encrypted text would have the same letter as the plaintext.).
Each rotor and each reflector implements a different permutation, and the overall effect depends on their configuration: which rotors and reflector are used, what order they are placed in the machine, and which rotational position they are initially set to. This configuration is the secret key used to encrypt or decrypt a message. On our simple machine, there are thus 614175744:
- Two possible reflectors times
- Two possible rotors in the fourth position, times
- $8!/(8-3)! = 336$ choices for the rightmost three rotors and their ordering, times
- $26^4$ possible initial rotational settings for the rightmost four rotors (each reflector has only one possible position.).
In what follows, we'll refer to the selected rotors in a machine's configuration as 1—5, with 1 being the reflector, and 5 the rightmost rotor.
Before a letter of a message is translated, a spring-loaded pawl (lever), one for each of rotors 3—5, tries to engage a ratchet on the right side of its rotor and to rotate that rotor by one position, thus changing the permutation performed by the rotor. The lever on the right rotor (5) always succeeds, so that rotor 5 (the "fast" rotor) rotates one position before each character. The pawls pushing rotors 3 and 4, however, are normally blocked from engaging their rotors by a ring on the left side of the rotor to their right (rotors 4 and 5 respectively). This ring holds the pawl away from its ratchet, preventing its wheel from moving, except when the pawl is positioned over a notch in the ring when the pawl moves. Each of the I—VIII rotors has at least one such notch (two in the case of rotors VI—VIII). A "feature" of the design (It was corrected in other versions of the Enigma, since it reduced the period of the cipher) is that when a pawl is in a notch, it also moves the notch and the wheel it is connected to, so that the rotors on both sides of the pawl move. This means that rotor 4 experiences "double stepping"---if it advances on one step so that its notch moves under the pawl to its left (belonging to rotor 3), then on the next step, when rotor 3 advances, its pawl also advances rotor 4 (even though rotor 4's own pawl has moved off the notch to its right on the previous move and does not contact the ratchet on rotor 4). This peculiarity only affects rotor 4: rotor 5 always advances anyway, and rotors 1 and 2 have no pawls and never move.
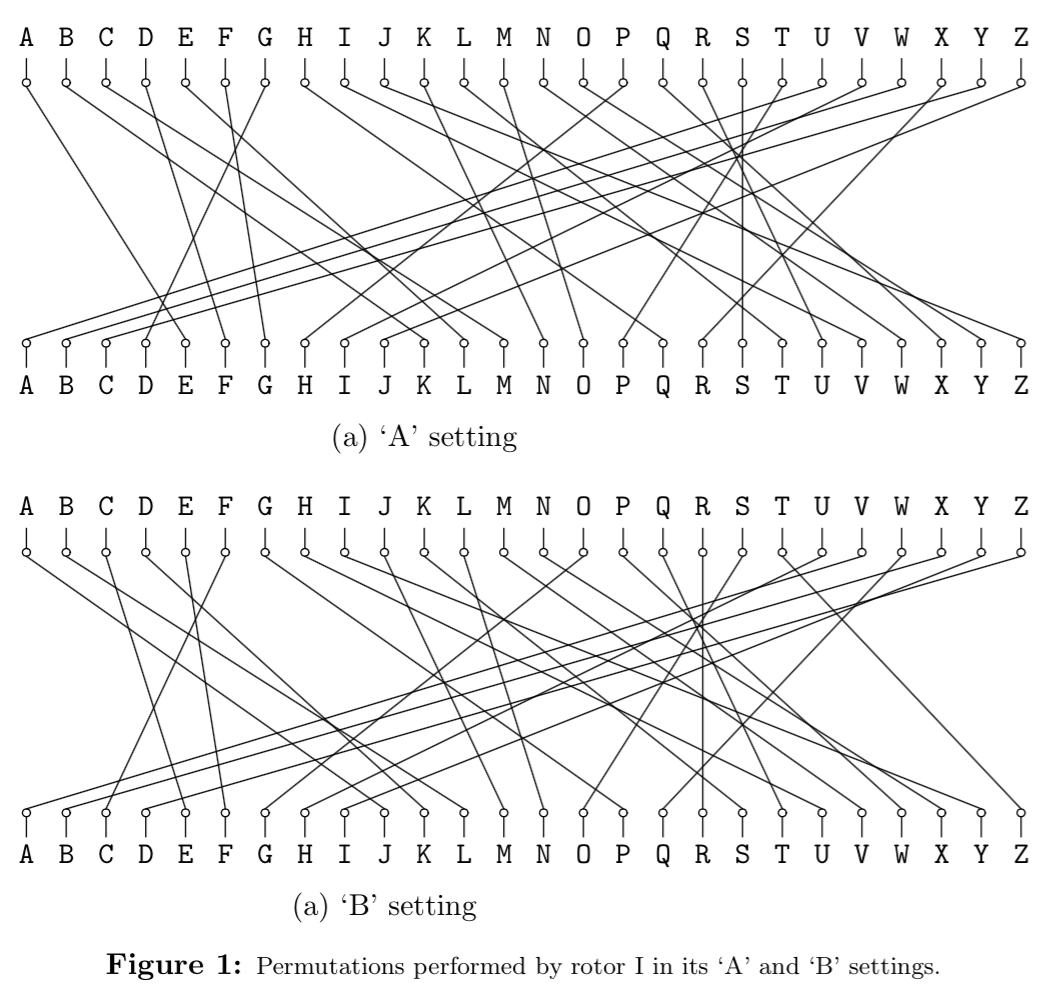
The effect of advancing a wheel is to change where on the wheel a certain signal enters or leaves. When a wheel is in its 'A' setting in the machine, then a signal that arrives at, say, the 'C' position, goes into the 'C' contact on the wheel. Likewise, a signal the leaves the wheel from its 'C' contact exits at the 'C' position. When the wheel is rotated by one to its 'B' setting, a signal that arrives at the 'C' position goes instead into the 'D' contact on the wheel, and a signal that leaves through the 'D' contact does so at the 'C' position. It's easier to see if we use numbers 0—25 rather than letters ('A' is 0, 'B' is 1, etc.). Then, when the wheel is in its $k$ setting, a signal entering at the $p$ position enters the $p+k \bmod 26$ contact on the wheel, and a signal exiting through the $c$ contact does so at the $c - k \bmod 26$ position. Figure 1 shows the effect of moving rotor I from its 'A' to its 'B' setting.
The contacts on the rightmost rotor's right side connect with stationary input and output contacts, which run to keys that, when pressed, direct current to the contact from a battery or, when not pressed, direct current back from the contact to a light bulb indicating a letter of the alphabet. Since a letter never encrypts or decrypts to itself, the to and from directions never conflict.
The operator can set the initial positions of the rotors using finger wheels on each rotor. Each rotor has an alphabet running around its perimeter and visible to the operator through the top of the machine. The letter that is showing at any given time indicates the setting of that rotor.
Example
As an example of a translation, suppose that the rotors in positions 1—5 are, respectively, B, Beta, III, IV, and I and assume that 2—5 are currently at positions A, X, L, E, respectively. We input the letter 'F', which causes the following steps:
- The pawls all move. This causes rotor 5 to advance from E to F. The other two pawls are not over notches, so rotors 3 and 4 do not move.
- The letter 'F' enters the right side of rotor 5 (an I rotor). Since this rotor is at position 'F' (letter number 5 of the alphabet, numbering from 0), the signal enters the rotor at position $5+5=10$, or 'K'.
- According to Figure 2, rotor I converts 'K' to 'N' (letter number 13). Because of the rotation of rotor I, however, the signal actually comes out at letter position $13-5=8$ ('I').
- The 'I' signal from rotor 5 now goes into the right side of rotor 4. Since rotor 4 is a IV rotor and is in the 'L' (or 11) position, the 'I' enters the $8+11=19$ ('T') position, and is translated to 'G' (6), which comes out at position $6-11=-5 = 21 \bmod 26$, the fifth letter from the end of the alphabet ('V').
- The 'V' from rotor 4 goes now to the right side of rotor 3, a III rotor in position 'X' (23). The signal enters the rotor at position $21+23 = 44 = 18 \bmod 26$ ('S'), is translated to 'G' (6), which exits at position $6 - 23 = -17 = 9 \bmod 26$ ('J').
- Rotor 2 (Beta) is in position 'A', and thus translates 'J' to 'W'.
- Rotor 1 (B) converts the 'W' to 'H' and bounces it back to the left side of rotor 2.
- Rotor 2 (Beta in the 'A' position) converts 'H' on its left to 'X' (23) on its right.
- The 'X' from rotor 2 now goes into the $23 + 23 = 46 = 20 \bmod 26$ ('U') position on the left side of rotor 3 (III in position 'X'), and is converted to 'W' (22), which comes out at position $22-23=-1=25 \bmod 26$ ('Z') on the right side of rotor 3.
- 'Z' now enters the left side of rotor 4 (IV in position 'L') at $25+11=36=10 \bmod 26$ ('K'), is translated to 'U' (20), which comes out at position $20 - 11=9$ ('J') on the right side of rotor 4.
- Finally, the 'J' from rotor 4 enters the left side of rotor 5 (I at position 'F') at position $9 + 5= 14$ ('O'), is translated to 'M' (12), and comes out at position $12 - 5 = 7$ ('H') on the right side of rotor 5.
Therefore, 'F' is converted to 'H'.
After a total of 12 characters are converted, the rotor settings will have become 'AXLQ'. Just before the next character is converted, rotor 5 will advance to 'R' and, since its notch is at position 'Q', rotor 4 will advance to 'M', so that the rotor configuration will be 'AXMR' before the 13th character is converted. After an additional 597 characters have been converted, the configuration will be 'AXIQ'. The character after that will advance rotor 5 to 'R' and rotor 4 to 'J', giving 'AXJR'. The next character will advance 5 to 'S', and, since rotor IV's notch is at 'J', rotor 3 will advance to 'Y'. Also, as rotor 3's pawl advances rotor 3, it also moves the notch on rotor 4, advancing rotor 4 to 'K', so that the configuration goes from 'AXJR' to 'AYKS'. Rotor 3 in this case has a notch at 'V', but since rotor 2 has no pawl, rotor 3's notch never has any effect.
Input and Output
To run your program, you can use the command
java enigma.Main [input file name] [output file name]The input to your program will consist of a sequence of messages to decode, each preceded by a line giving the initial configuration. A configuration line looks like this:
* B BETA III IV I AXLE(all upper case.) This particular example means that the rotors used are reflector B, and rotors Beta, III, IV, and I, with rotor I in the rightmost, or fast, slot. Rotor 1 is always the reflector; rotor 2 is Beta or Gamma, and each of 3—5 is one of rotors I—VIII. A rotor may not be repeated. The last four-letter word gives the initial positions of rotors 2—5 (i.e., not including the reflector,) in the same order as they were specified.
After each configuration line comes a message on any number of lines. Each line of a message consists only of letters, blanks, and tabs (0 or more). The program should ignore the blanks and tabs and convert all letters to upper case. The end of message is indicated either by the end of the input or by a new configuration line (distinguished by its leading asterisk). The machine is not reset between lines, but continues stepping from where it left off on the previous message line. Because the Enigma is a reciprocal cipher, a given translation may either be a decryption or encryption; you don't have to worry about which, since the process is the same in any case.
Output the translation for each message line in groups of five upper-case letters, separated by blanks (the last group may have fewer characters, depending on the message length). Figure 3 contains an example that shows an encryption followed by a decryption of the encrypted message. Since we have yet to cover the details of File I/O, you will be provided the File IO machinery for this project.

Handling Errors
You can see a number of opportunities for input errors:
- The input might not start with a configuration.
- The configuration line can contain the wrong number of arguments.
- The rotors might be misnamed.
- A rotor might be repeated in the configuration.
- The first rotor might not be a reflector.
- The initial positions string might be the wrong length or contain non-alphabetic characters.
- The message might contain non-alphabetic characters.
A significant amount of a program will typically be devoted to
detecting such errors, and taking corrective action. In our case, the
only corrective action needed is throwing an EnigmaException with an explanatory message.
Testing
To help with testing some basic functionalities of your project, we have provided
you with a couple of JUnit test cases in the file SanityCheckTest.java. After setting
up JUnit, you should be able to run these tests from the command line using
$ java org.junit.runner.JUnitCore tests.SanityCheckTestor from IntelliJ using its built-in JUnit testing capabilities. In addition, we encourage you to extend the provided tests with some test cases of your own. While it may be tempting to follow ADD (in other words, Autograder-driven Development), you'll likely have a much better time testing your project locally rather than waiting in a queue.
What to Turn In
Submit your project by pushing to github.
You may change any of the code we've provided, as long as the resulting program works according to the specifications here.
Your finished programs should be workmanlike, and of course, we will enforce the mechanical style standards. Make sure all methods are adequately commented---meaning that after reading the name, parameters, and comment on a method, you don't need to look at the code to figure out what a call will do.
Don't leave debugging print statements lying around. In fact, don't use them; learn to use the debugger.
Advice
First, get started immediately, of course. Don't just jump in and code, though. Make sure you understand the specifications (which have their subtleties) and plan out how you're going to meet them. Read the skeleton code and understand the design. Figure out how to break this problem down into small pieces, and how to implement and test them one piece at a time. Know in detail how you're going to do something before writing a line of Java code for it. In particular, take some time to understand how the rotors work, and especially how the rotor position modifies the permutation.
Don't allow things to remain mysterious to you, or they'll surely bite
you at some point. You don't have to use any of the skeleton
code we've provided as long as the command java enigma.Main
works as specified. However, if you find yourself throwing something
away because you don't understand it, STOP! You're allowing
yourself to be mystified by something that is intended to be simple.
There is a fair amount of string-hacking involved.
The Java library can help you. Look at the documentation of
String, Character, and perhaps
java.util.regex.Pattern
in the on-line Java library documentation.
We particularly invite you to consider
| From String | From Character |
|---|---|
| charAt | isLetter |
| replaceAll | isWhitespace |
| split | |
| startsWith | |
| substring | |
| toUpper | |
| trim |
A useful property of characters is that the type char is
actually an integer type, and that if c is an upper-case letter,
then c - 'A' is the position of c in the alphabet ('A' is
0, 'B' is 1, etc.). Contrariwise, if p is the position of an
upper-case letter in the alphabet, then (char) (p + 'A') is the
corresponding character.
Be creatively lazy. Feel free to browse the Java library for useful
stuff, even if you haven't seen it in class. For example, you might
find a use for HashMap or ArrayList.
If you find yourself writing:
if (rotor.equals("I") {
if (c == 'A')
e = 'E';
else if (c == 'B')
e = 'K';
...
}or something equally hideous, STOP! you are doing something wrong!
You can write JUnit tests of the overall system before you write a line of code. Be particularly careful to include tests that at one point caused your program to fail (regression tests) so that you can be sure you don't backslide when you make further changes. There's no reason you can't have tests that you fail, by the way; they'll serve to remind you of things you still need to do.
Use the git repository. Frequently commit your work so that you'll never have to reconstruct too much if your files somehow vanish mysteriously.
Above all, it is always fair to ask for help and advice. We don't ever want to hear about how you've been beating your head against the wall over some problem for hours. If you can't make progress, don't waste your time guessing or bleeding: ask. If nobody's available to ask, do something else (or get some sleep).