Lab 8: Abstract Data Types & Interfaces

Before You Begin

Pull the code for Lab 8 and create a new IntelliJ project for it.

Learning Goals

Today we’re going to learn about the more advanced features of Java’s inheritance system, namely Abstract Classes and Interfaces. These two constructs allow us to make a more complicated system of class interrelations than we have seen previously, and the correct utilization of both concepts is key to being able to write generalizable and neat code.

Once introduced, we will use these two concepts to explain the workings of the Java Collections Framework, to which many of the data structures you have encountered belong. Finally, we’ll get a chance to work with some of these data structures to solve practical problems.

Introduction

Read Chapter 4.1, 4.4, and 5.2 of the online textbook. The textbook provides motivation for learning interfaces and abstract classes, though we’ll first jump back and gets some hands-on experience defining classes with interfaces and abstract classes before jumping deeper into solving problems with abstract data types.

In the first two weeks of CS 61BL, we’ve implemented the list abstract data type using two, different underlying data structures: linked lists and resizing arrays. We’ve seen that SLList/DLList and AList share quite a few of the same methods. While we didn’t implement all of the methods for both classes, we should now have a good idea of how we might go about it on our own.

public void add(int index, Item item);
public void addFirst(Item item);
public void addLast(Item item);
public Item get(int index);
public Item getFirst();
public Item getLast();
public void remove(Item item);
public Item removeFirst();
public Item removeLast();
public int size();

Exercise: `GregorianDate`

Let’s start with an example of an abstract class. Date.java is an abstract class used to represent calendar dates (we will ignore leap years). In addition, we have included two classes that extend Date that are shown below.

/**
 * In a nonleap year in the French Revolutionary Calendar, the first twelve
 * months have 30 days and month 13 has five days.
 */
public class FrenchRevolutionaryDate extends Date {

    public FrenchRevolutionaryDate(int year, int month, int dayOfMonth) {
        super(year, month, dayOfMonth);
    }

    @Override
    public int dayOfYear() {
        return (month - 1) * 30 + dayOfMonth;
    }

    ...
}

public class GregorianDate extends Date {

    private static final int[] MONTH_LENGTHS = {
        31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
    };

    public GregorianDate(int year, int month, int dayOfMonth) {
        super(year, month, dayOfMonth);
    }

    @Override
    public int dayOfYear() {
        int precedingMonthDays = 0;
        for (int m = 1; m < month; m += 1) {
            precedingMonthDays += getMonthLength(m);
        }
        return precedingMonthDays + dayOfMonth();
    }

    private static int getMonthLength(int m) {
        return MONTH_LENGTHS[m - 1];
    }
}

Add an abstract method named nextDate to the Date class. nextDate returns the new date that is the result of advancing this date by one day. It should not change this. Then, modify GregorianDate accordingly so that it follows the correct convention for dates. Make sure to test out your methods to be sure that they behave as you expect them to!

Interfaces

When a class implements an interface, it is giving a guarantee that it can perform a certain functionality, as defined by the interface it implements. You’ll find that the idea of an interface is actually very central to software engineering in general. When you’re asked to implement a set of methods to perform some specific task, that’s implementing an interface. Often when working on a group project, a good approach is to split the work into parts that will be integrated together at the end. In order to allow work to be done in parallel, it is important to establish what each part will accomplish and how it will interact with other parts so that they can be merged together without issue. Establishing what each of these parts will do and how they interact with other parts is essentially treating each part as an interface. Using interfaces is all about not knowing the actual implementation, but instead utilizing the input-to-output, defined behavior given by the interface; implementing an interface to specification like you are asked for assignments and projects is about making sure the program you write under some interface gives the correct output for all inputs.

Collections

Collection classes represent collections of data. Most of the data structures we will study the rest of this class are used to implement collections. At the most general level, pretty much anything you use to store multiple items at once is going to fulfill the requirements to be a collection. The most commonly used collections are lists, sets, and maps, but there are many others.

All collections are organized into an inheritance hierarchy. At the root is the top-level Collection interface. This interface specifies methods like isEmpty(), or add(T o) (generic type T), among many others

All collection classes implement Collection in one way or another. Each of List, Set, and Map support their own set of key operations. In this lab, we’ll take a closer look at the Java Set, Map, and List collection interfaces.

The `List` Interface

A list is an ordered collection, or sequence, so the elements in a list have positions. An element can appear as many times as desired as duplicates are allowed. Thus, they support the following operations:

Adding an element at a given position or at the end of the list.
Removing an element at a given position or at the end of the list.
Checking whether a given item is in the list.
Returning the value at a given position in the list.

Implementation of a list normally involves storing the elements of the list explicitly, like we implemented in our linked lists and resizing array lists.

It’s important to realize that List, although a sub-interface of Collection, is itself an interface, and might be defined like this:

public interface List<Item> extends Collection<Item> {
    ...
}

The `Set` Interface

A set is a group of items with no duplicates. The Set interface does not require ordering (Java’s HashSet), but some set implementations can be ordered (Java’s TreeSet). Sets support at least the following operations:

Adding an element to the set if it’s not already there.
Removing an element from the set.
Checking whether a given item is in the set.

Without the additional requirement of maintaining order, sets can often be more efficient than lists, and we’ll implement one example that demonstrates the difference later in this lab.

The Set interface might be declared like this,

public interface Set<Item> extends Collection<Item> {
    ...
}

The `Map` Interface

A map is a collection of key-value mappings, like a dictionary from Python. Like a set, the keys in a map are unique. Maps also do not need to maintain order (Java’s HashMap), but some map implementations can be orered (TreeMap, for example). Maps support at least the following operations:

Adding a key-value pair to the map, or updating the value if the key already exists.
Removing a key-value pair from the map.
Checking whether a given key is in the map.
Returning the value associated with a given key.

The same reason that sets can be implemented more efficiently than lists also applies to maps. A map can also be thought of as a set whose item, instead of just being a single object like Item, is instead a pair of items.

public interface Map<Key, Value> {
    ...
}

Unlike set and list, Map is not a direct sub-interface of the Java Collection interface. This is because Collection specifies collections of a single element type, but Map operates on key-value pairs. Instead, “The Map interface provides three collection views, which allow a map’s contents to be viewed as a set of keys, collection of values, or set of key-value mappings.”

keySet(), which returns a Set of all the keys. The keys are unique, so a set is an appropriate choice here.
values(), which returns a Collection of all the values. The values are not necessarily unique, which is why we prefer a more general Collection rather than a Set.
entrySet(), which returns a Set of key-value pairs with a wrapper type called Entry. The entry class’s job is just to hold the key and the value together in a single class, so you can imagine that it might look something like this.
```
  public static class Entry<Key, Value> {
      private Key key;
      private Value value;

      ...
  }
```

Exercise: `CodingChallenges`

Knowing when, where, and how to use abstract data types is an important skill.

For this part, we’ll be using abstract data types to help us solve small programming challenges. These questions are similar to the kinds of questions you might get asked to solve in a technical interview for a software engineering position. Complete the methods outlined in CodingChallenges.java.

Since all of the abstract data types in Java are interfaces, we’ll need a few concrete implementations to actually use them. For this lab, it’s fine to use the following initializations. We’ll be learning more about each of these concrete classes in future labs.

For these problems you might notice that there isn’t necessarily just one way to solve the problem. Try to reason through the runtime for each approach and choose the one which gives the best possible runtime. We list the runtime for common operations in each class below, where $N$ is the asymptotic variable representing the size of the collection.

List

For lists, use ArrayList. This is our resizing array list except with a couple of additional enhancements that we’ll be learning more about next week.

  List<String> list = new ArrayList<>();

add(int index, E element): $O(N)$ .
add(E e): $O(N)$ , but usually $\Theta(1)$ .
contains(Object o): $O(N)$ .
remove(int index): $O(N)$ .
remove(Object o): $O(N)$ .

Set

For sets, use HashSet. HashSet has the unique advantage over ArrayList of having usually constant-time operations, for reasons we’ll explore later in this lab with BooleanSet and later in a few weeks when we learn about hashing.

  Set<String> set = new HashSet<>();

add(E e): $O(N)$ , but usually $\Theta(1)$ .
contains(Object o): $O(N)$ , but usually $\Theta(1)$ .
remove(Object o): $O(N)$ , but usually $\Theta(1)$ .

Map

For maps, use HashMap. Like a HashSet, most operations are usually constant time, but it has the advantage of supporting the Map interface.

  Map<String, Integer> map = new HashMap<>();

containsKey(Object key): $O(N)$ , but usually $\Theta(1)$ .
containsValue(Object value): $O(N)$ and not much better than that due to linear search through the data structure.
get(Object key): $O(N)$ , but usually $\Theta(1)$ .
put(K key, V value): $O(N)$ , but usually $\Theta(1)$ .
remove(Object key): $O(N)$ , but usually $\Theta(1)$ .

For more information on what methods are available in each class, search online for the Java documentation. Use IntelliJ to help you import classes as you need them.

If you’d like extra practice, there are a few optional problems in ExtraCodingChallenges.java.

Exercise: `BooleanSet`

The file SimpleCollection.java contains a simplified version of the Collection interface which only accepts integers as members. The files SimpleSet.java and SimpleList.java contain simplified versions of the Set and List collection interfaces. Read all three files so you can understand how interfaces and inheritance are being used here, as well as to understand what each of the interfaces require.

Earlier, we implemented an array-based list, AList, which supported automatic resizing and generics. For this lab, we’ll be using the same underlying array data structure except now we’ll be using it to implement the new set abstract data type.

The file BooleanSet.java is an incomplete implementation of the SimpleSet interface. It maintains uniqueness of elements in the set by storing a boolean array contains. This version of the SimpleSet interface only deals with positive integers and uses a boolean array to keep track of what values are currently in the Set. Check the example below:

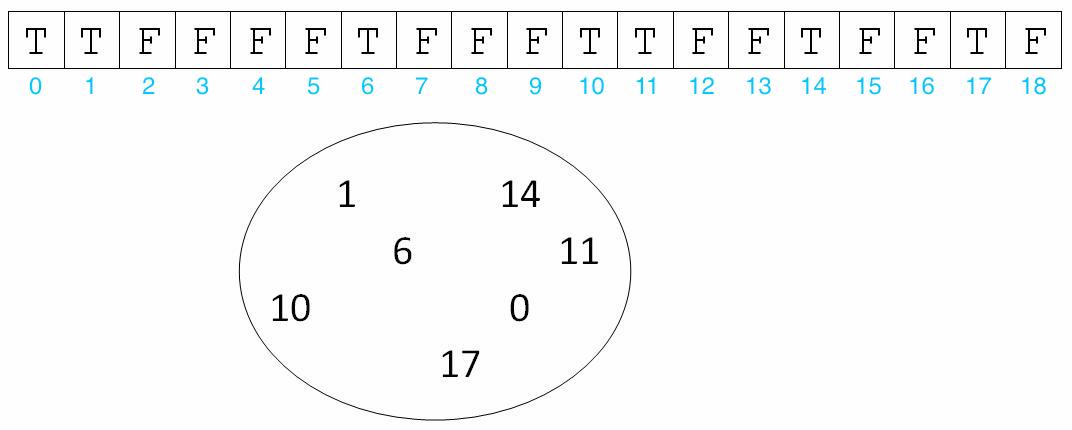
BooleanSet array

Implement the methods of the BooleanSet.java class, and use the BooleanSetTest.java file to test your methods. We only provide a basic test, so feel free to add more comprehensive tests to this file.

Generics and Autoboxing

Read Chapter 5.1 and 5.3 which we skipped earlier, covering generics and autoboxing in Java. These two topics will be helpful for implementing data structures in the next segment of the course, though these topics won’t be emphasized in this lab.

Recap

We introduced a few key topics in this lab: inheritance, abstract classes, and interfaces, and we saw how each of these Java features could be used to help us implement abstract data types.

Abstract Data Types

Previously, we went over interfaces which, in a traditional sense (disregarding default methods which will be defined a bit lower), requires certain methods to be implemented in a class if it is said a type of that interface. Abstract Data Types follow this philosophy, and are defined to be some sort of Object that is defined by some set of operations rather than the implementation of these operations.

Interfaces

There are 2 types of inheritance that we have gone over in previous lectures:

Interface inheritance: What (the class can do).
Implementation inheritance: How (the class does it).

Default Methods

The way we have dealt with interfaces, there is no content in them. We only define a certain set of operations that need to be fulfilled by anything that implements the interface. However, we can create default methods that take the following form:

  default void methodName(){...}

Normal interface methods have no body and only state what needs to be defined. Default methods on the other hand provide how a method by providing a method body.

Variables can exist in interfaces but they are public static final.
Classes can implement more than 1 interface.
Methods are public unless stated otherwise
Interfaces cannot be instantiated.

Abstract Classes

Abstract classes can be thought of as a hybrid of a normal class and an interface. Abstract classes are like interfaces in that they cannot be instantiated. All methods in an Abstract class are like normal methods in classes unless they have word abstract in front of them. If that is the case then they are treated like normal methods in interfaces and do not need to have a body and can instead have an implementation in whatever class extends them. A very important difference between abstract classes and interfaces is that a class can only extend one abstract class but can implement more than one interface.

Immutability

Immutable data types are types that cannot change. To make sure that a variable does not change, use the final keyword. Once a variable is declared final, it can never change after initial assignment. An important note is that if an address is declared final it means that the address can’t change: it says nothing about its contents. For example the below syntax is valid.

  final int[] arr = new int[1];
  arr[0] = 1;
  arr[0] = 3

But this one is not:

  final int[] arr = new int[3];
  arr = new int[4];

Because you are changing the address of the actual array the variable is pointing to.

Deliverables

Here’s a quick summary of what you need to do for this lab:

Add an abstract method nextDate to the Date class and implement GregorianDate.nextDate.
Solve the programming puzzles in CodingChallenges.java.
Implement and test each method in BooleanSet.java.

There’s no assessment for this lab. However, you’ll still need to complete the weekly self-reflection to receive full credit on the lab.