Lab 21: Heaps and Priority Queues

Introduction

As usual, pull the files from the skeleton and make a new IntelliJ project.

We’ve learned about a few abstract data types already, including the stack and queue. The stack is a last-in-first-out (LIFO) abstract data type where, much like a physical stack, one can only access the top of the stack and must pop off recently added elements to retrieve previously added elements. The queue is a first-in-first-out (FIFO) abstract data type. When we process items in a queue, we process the most recently added elements last.

But what if we want to model an emergency room, where people waiting with the most urgent conditions are served first? We would need to serve patients regardless of when they arrive, since those arriving first or most recently will not necessarily be the ones most in pain.

Sometimes, processing items LIFO or FIFO is not what we want. We may instead want to process items in order of importance or a priority value.

The priority queue is an abstract data type that contains the following methods:

insert(item, priority): Inserts item into the priority queue with priority value priority.
poll: Removes and returns the highest priority item in the priority queue.
peek: Returns the highest priority item.

It is similar to a Queue though the insert method will insert an item with a corresponding “priority value” and the poll method in the priority queue will remove the element with the highest priority, rather than the oldest element in the queue.

Note: The element with the highest priority may not always have the highest priority value. Priorities are a function of priority values: if we have a maximum priority queue, the elements with higher priority will be the ones with larger priority values; on the other hand, if we have a minimum priority queue, the elements with higher priority will be the ones with smaller priority values.

Exercise: PQ Implementations

For the following exercises, we will think about the underlying implementations for our priority queue. Choose from the following runtimes:

$\Theta(1), \Theta(\log N), \Theta(N), \Theta(N \log N), \Theta(N^2)$

Discuss with your partner, and submit your answers to the Gradescope assessment.

Note: For these exercises, each item will be associated with a priority value, and we will prioritize items with the smallest priority value first.

Exercise 1: Unordered Linked List

Considering the implementation of a priority queue with an unordered linked list of $N$ elements, determine the runtime for each scenario.

In the worst case, describe the runtime to insert an item into the priority queue.
In the worst case, describe the runtime to remove the element with highest priority.

Exercise 2: Ordered Linked List

Considering the implementation of a priority queue with an ordered linked list of $N$ elements, determine the runtime for each scenario.

In the worst case, describe the runtime to insert an item into the priority queue.
In the worst case, describe the runtime to remove the element with highest priority.

Exercise 3: Balanced Binary Search Tree

Considering the implementation of a priority queue with a balanced binary search tree of $N$ elements, determine the runtime for each scenario.

In the worst case, describe the runtime to insert an item into the priority queue.
In the worst case, describe the runtime to remove the element with highest priority.

But can we do better?

Java’s priority queue is actually implemented with a data structure called a binary min heap. For the remainder of this lab, we will study the heap data structure and create our own implementation of a priority queue using a binary min heap.

Heaps

Having a fast implementation of a priority queue would be very helpful, but as we saw in the last exercise, each of the implementations we tried has flaws. Instead, let’s take a closer look at the data structure Java uses to implement its priority queue.

The heap is a tree-like data structure that will help us implement a priority queue with fast operations. In general, heaps will organize elements such that the lowest or highest valued element will be easy to access. To use a heap as the underlying implementation of a priority queue, we can use the priority values that each of the priority queue’s items are associated with as the elements inside our heap. This way, the lowest or highest priority value object will be at the top of the heap, and the peek operation will be very fast.

There are two flavors of heaps: min heaps and max heaps. They’re very similar except that min heaps keep smaller elements towards the top of the heap, and max heaps keep larger elements towards the top. Whichever heap (min or max) that is used as the underlying structure of the priority queue will determine what kind of values inside the heap will correspond to a higher priority. For example, if one uses a min heap as the underlying representation of a priority queue, then smaller priority values will be kept at the top of the heap. This means that priority is given to objects with smaller priority values. This is also how Java’s PriorityQueue organizes its objects under the hood!

Let’s now go into the properties of heaps.

Heap Properties

Heaps are tree-like structures that follow two additional invariants. Elements in a heap can have any number of children, but we will restrict our view to binary heaps where each element will have only two children. Thus, binary heaps are essentially binary trees with two extra invariants. However, it is important to note that they are not binary search trees.

The invariants are listed below.

Invariant 1: Completeness

In order to keep our operations fast, we need to make sure the heap is well balanced. We will define balance in a binary heap’s underlying tree-like structure as completeness.

A complete tree has all available positions for elements filled, except for possibly the last row, which must be filled left-to-right. A heap’s underlying tree structure must be complete.

Here are some examples of trees that are complete:

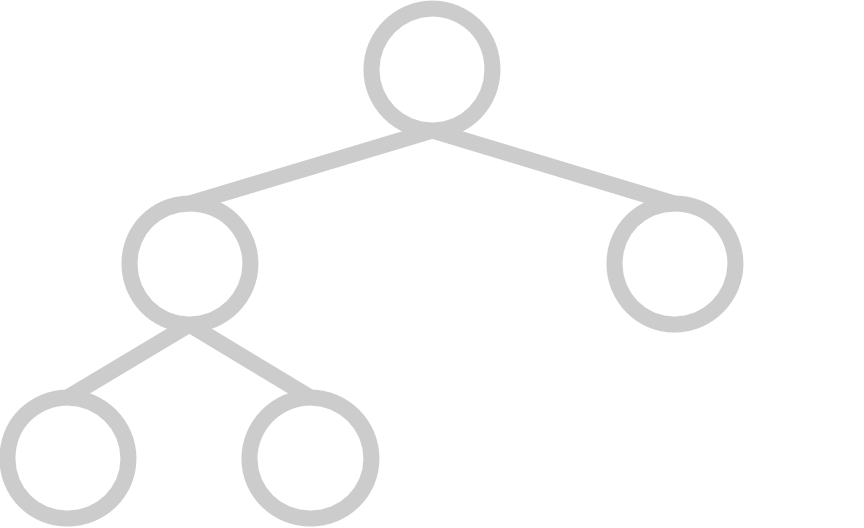And here are some examples of trees that are not complete:

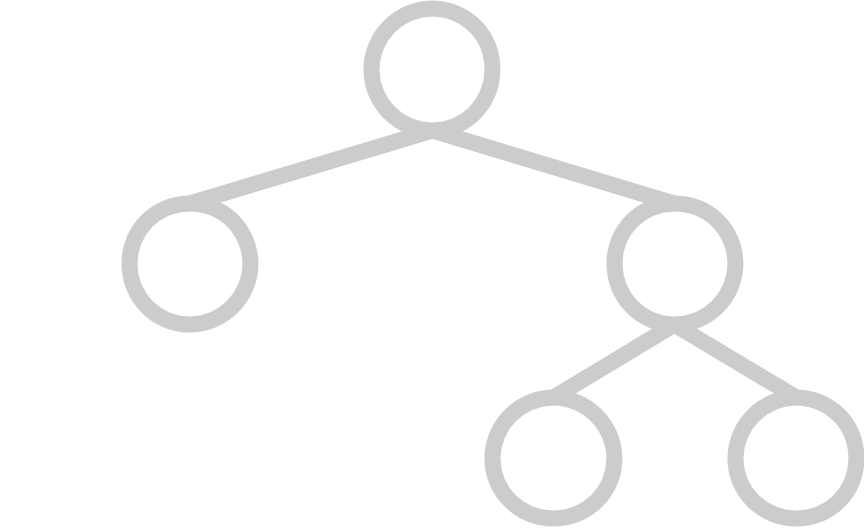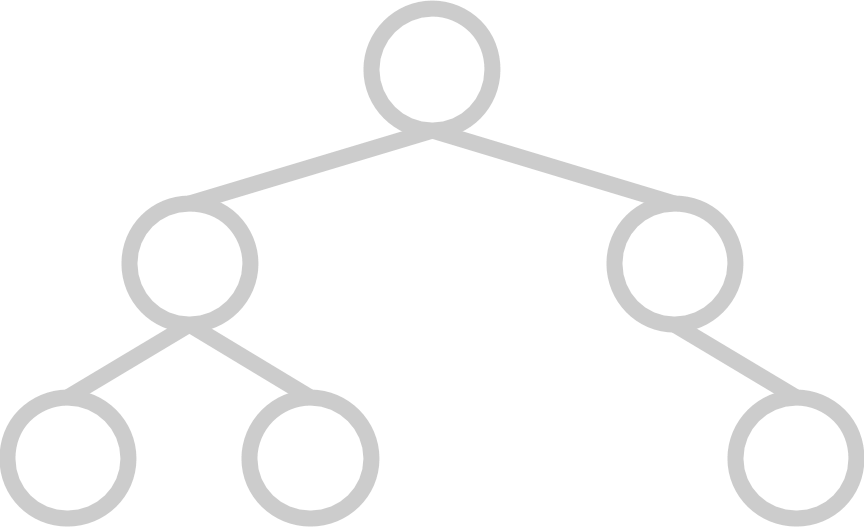Invariant 2: Heap Property

We will also introduce another property that will allow us to organize the heap in a way that will result in fast operations.

Every element must follow the heap property, which states that the value of element $E$ must be smaller than those of all of its children or larger than those of all of its children. The former is known as the min-heap property, while the latter is known as the max-heap property.

If we have a min heap, this guarantees that the element with the lowest value will always be at the root of the tree. If the elements are our priority values, then we are guaranteed that the lowest priority valued element is at the root of the tree. This helps us access that item quickly, which is what we need for a priority queue!

For the rest of this lab, we will be discussing operations in terms of binary min heaps. However, this logic can be applied to max heaps or heaps with any number of children.

Representation

In previous labs, we discovered that lists could be implemented using arrays or linked nodes. Then, when we learned about disjoint sets, we saw that they could be represented by both arrays and linked nodes too. It turns out that this dual representation extends to trees as well! Trees are generally implemented using nodes with parent and child links, but they can also be represented using arrays.

Here’s how we implement a binary tree using an array:

The root of the tree will be in position 1 of the array (nothing is at position 0; this is to to make indexing more convenient).
The left child of a node at position $N$ is at position $2N$ .
The right child of a node at position $N$ is at position $2N + 1$ .
The parent of a node at position $N$ is at position $N / 2$ .

Because binary heaps are essentially binary trees, we can use this array representation to represent our binary heaps!

Exercise: PQ Representation

In the MinHeap.java class that has been provided for you, implement the binary tree representation discussed above by implementing the following 6 methods:

private int getLeftOf(int index);
private int getRightOf(int index);
private int getParentOf(int index);
private int min(int index1, int index2);

Our code will use an ArrayList instead of an array so we will not have to resize our array manually, but the logic is the same.

Discussion: `contains`

In our MinHeap, the node objects are contained in an ArrayList called contents. Code for a hypothetical contains method is shown below.

public boolean contains(E value) {
    for (E element : contents) {
        if (element != null && element.equals(value)) {
            return true;
        }
    }
    return false;
}

The contains method runs in time proportional to what in the worst case?

Discuss with your partner, and pick one of the following answers and submit to the Gradescope assessment.

$h$ , the height of the tree
$n$ , the number of nodes in the tree
$l$ , the length of the array that contains the tree

Heap Operations

For min heaps, there are three operations that we care about:

insert: Inserting an element to the heap.
removeMin: Removing the item with the lowest value. This would correspond to removing the highest priority element in the corresponding priority queue.
peek: Returning the lowest value without removal. This would correspond to accessing the highest priority element in the corresponding priority queue.

When we do these operations, we need to make sure to maintain the invariants mentioned earlier (completeness and the heap property). Let’s walk through how to do each one.

`insert`

Put the item you’re adding in the next available spot in the bottom row of the tree. If the row is full, make a new row. This is equivalent to placing the element in the next free spot in the array representation of the heap. This ensures the completeness of the heap because we’re filling in the bottom-most row left to right.
If the element that has just been inserted is N, swap N with its parent as long as N’s value is smaller than its parent’s value or until N is the new root. This is called bubbling up, and this ensures the min-heap property because once we finish bubbling up the element, all elements below it must be greater than it, and all elements above must be less than it.

`removeMin`

Swap the element at the root with the element in the bottom rightmost position of the tree. Then, remove the right bottommost element of the tree (which should be the previous root and the minimum element of the heap). This ensures the completeness of the tree.
If the new root N is greater than either of its children, swap it with that child. If it is greater than both of its children, choose the smaller of the two children. Continue swapping N with its children until it is smaller than its children or it has no children. This is called bubbling down, and this ensures the min-heap property since we stop bubbling down only when the element N is less than both of its children and also greater than its parent.

`peek`

The element with the smallest value will always be stored at the root due to the min-heap property. Thus, we can just return the root node, without changing the structure of the heap.

Exercise: Heap Operations

Now, fill in the following missing methods in MinHeap.java:

public E peek();
private void bubbleUp(int index);
private void bubbleDown(int index);
public void insert(E element);
public int size();
public E removeMin();

When you implement insert and removeMin, you should be using bubbleUp and/or bubbleDown, and when you implement bubbleUp and bubbleDown, you should be using getLeft, getRight, getParent, min, and swap.

Playing with Heaps

We just covered a lot of new concepts for heaps. To test yourself and see if you understand them, try drawing a heap. Draw what happens when you insert numbers into the heap and when you remove the smallest (or biggest, depending on if the heap is a max or min heap) element. Discuss the results with your partner.

Also, take a look at the USFCA interactive animation of a min heap. You can type in numbers to insert, or remove the min element (ignore the BuildHeap button for now; we’ll talk about that later this lab) and see how the heap structure changes.

You can use this animation to check your own drawings too—there is no ambiguity when constructing heaps, so if you insert numbers in the same order, yours should look exactly the same as this animation.

Exercise: `MinHeapPQ`

Now let’s use the MinHeap class that we created earlier to implement our own priority queue!

Take a look at the code provided for MinHeapPQ, a class that implements the PriorityQueue interface. Then, implement the methods of the interface (duplicated below) of the MinHeapPQ class

public T peek();
public void insert(T item, double priority);
public T poll();
public void changePriority(T item, double priority);
public int size();

For the changePriority method, you may want to implement the update method from the MinHeap class!

Exercise: Heap Brainteasers

Now, let’s get into some deeper questions about heaps.

For all the following questions, discuss with your partner and submit your answer to the Gradescope assessment.

Exercise 1: Heaps and BST’s

Consider binary trees that are both max heaps and binary search trees.

How many nodes can such a tree have? Choose all that apply.

1 node
2 nodes
3 nodes
4 nodes
5 nodes
Any number of nodes
No trees exist

Exercise 2: Determining Completeness

It’s not obvious how to verify that a linked binary tree is complete. A CS 61BL student suggests the following recursive algorithm to determine if a tree is complete:

A one-node tree is complete.
A tree with two or more nodes is complete if its left subtree is complete and has depth $k$ for some $k$ , and its right subtree is complete and has depth $k$ or $k - 1$ .

Here are some example trees. Think about whether or not the student’s proposed algorithm works correctly on them.

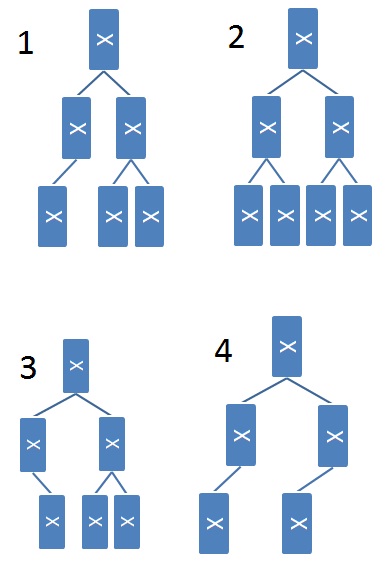
sample-trees

Choose all that apply to test your understanding of the proposed algorithm.

Tree 1 is complete
Tree 1 would be identified as complete
Tree 2 is complete
Tree 2 would be identified as complete
Tree 3 is complete
Tree 3 would be identified as complete
Tree 4 is complete
Tree 4 would be identified as complete

Discussion: Complete Trees and BFS

Another CS 61BL student claims that a binary tree is complete if all the leaves in the tree come at the end of a breadth-first traversal of the tree. Discuss with your partner to come up with counterexample to this claim.

Exercise 3: The Third Biggest Element in a Max Heap

Here’s an example max heap.

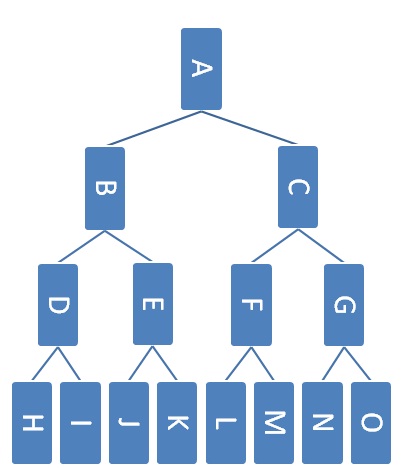
third-largest

Which nodes could contain the third largest element in the heap assuming that the heap does not contain any duplicates?

Node A
Node B
Node C
Node D
Node E
Node F
Node G
Node H
Node I
Node J
Node K
Node L
Node M
Node N
Node O

Which nodes could contain the third largest element in the heap assuming that the heap can contain duplicates?

Node A
Node B
Node C
Node D
Node E
Node F
Node G
Node H
Node I
Node J
Node K
Node L
Node M
Node N
Node O

Heapsort

Now, let’s move onto an application of the heap data structure. Suppose you have an array of $N$ numbers that you want to sort smallest-to-largest. One algorithm for doing this is as follows:

Put all of the numbers in a min heap.
Repeatedly remove the min element from the heap, and store them in an array in that order.

This is called heapsort.

Now, what is the runtime of this sort? Since each insertion takes proportional to $\log N$ comparisons once the heap gets large enough and each removal also takes proportional to $\log N$ comparisons, the whole process takes proportional to $N \log N$ comparisons.

It turns out we can actually make step 1 of heapsort run faster—proportional to $N$ comparisons—using a process called heapify. (Unfortunately, we can’t make step 2 run any faster than $N \log N$ , so the overall heapsort must take $N \log N$ time.)

Heapify

The algorithm for taking an arbitrary array and making it into a min (or max) heap in time proportional to $N$ is called heapify. Pseudocode for this algorithm is below:

def heapify(array):
    index = N / 2
    while index > 0:
        bubble down item at index
        index -= 1

Conceptually, you can think of this as building a heap from the bottom up. To get a visualization of this algorithm working, click on the BuildHeap button on USFCA interactive animation of a min heap. This loads a pre-set array and then runs heapify on it.

Try to describe the approach in your own words. Why does the index start at the middle of the array rather than the beginning, 0, or the end, N? How does each bubble down operation maintain heap invariants?

It is probably not immediately clear to you why this heapify runs in $O(N)$ . For those who are curious, you can check out an explanation on Wikipedia.

Conclusion

In today’s lab, we learned about another abstract data type called the priority queue. Priority queues can be implemented in many ways, but it is often implemented with a binary min heap. It is very easy to conflate the priority queue and the heap data structure, so make sure to understand the difference between the two!

Additionally, we learned how to represent a heap with an array, as well as some of its core operations. We then explored a few conceptual questions about heaps and learned about a new sort that this new data structure provides, heapsort.

All in all, priority queues are an integral component of many algorithms for graph processing (which we’ll cover in a few labs). For example, the first few weeks of CS 170, Efficient Algorithms and Intractable Problems, typically involve graph algorithms that use priority queues. Look out for priority queues in other CS classes as well! You’ll find them invaluable in the operating systems class CS 162, where they’re used to schedule which processes in a computer to run at what times.

Deliverables

To receive credit for this lab:

Complete MinHeap.java
Complete MinHeapPQ.java
Submit the Gradescope assessment.