Introduction
There is no worksheet for this lab. The coding submission will be worth the full 3 points for today.
As usual, pull the files from the skeleton and make a new IntelliJ project. You make work with any partner you choose today, and you may work either in your personal repository, or on a shared repository today. Remember that everyone needs to make their own Gradescope submission, but your code may be similar or identical to that of your partner.
In this lab, we will introduce another data structure called a tree. The meaning of the tree data structure originates from the notion of a tree in real life.
Below is a conceptual visualization of a tree. It’s not really a box and pointer diagram and should not be interpreted as a literal implementation in Java.
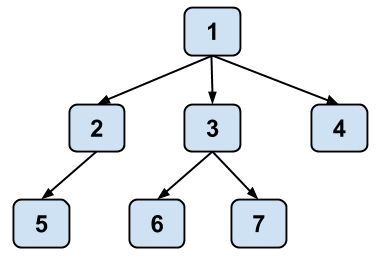
Note that while a tree in real life is rooted at the bottom and branches out and upwards, trees in computer science are typically drawn such that they are rooted at the top and branch out and downwards.
Vocabulary
In order to be able to talk about trees, we first need to define some terminology.
| Term | Description | Example Above |
|---|---|---|
| Node | Single element in a tree | 1, 2, 3, 4, 5, 6, and 7 are all nodes. |
| Edge | A connection between two nodes | There is a direct edge from 1 to 2, but there is no direct edge from 1 to 7. |
| Path | A series of one or more edges that connects two nodes without using an edge more than once | There is a path from 1 to 7, consisting of edges 1 -> 3 and 3 -> 7. |
| Leaf | A node with no children | 4, 5, 6, and 7 are leaf nodes. |
| Root | The topmost node, which does not have a parent | 1 is the root node. |
Relationships
These following terms are defined with respect to a particular node.
| Term | Description |
|---|---|
| Child | A node directly below the current node |
| Parent | Single node connected directly above the current node |
| Siblings | Nodes with the same parent |
| Ancestors | All nodes on the path from the selected node up to and including the root |
| Descendants | All the children, children’s children, and so forth of a node |
| Subtree | The tree consisting of the node and all of its descendants |
| Height | The length of the path from the node to its deepest descendant. By length, we mean the number of nodes traveled along a given path. Therefore, the height of a leaf node is 1. (Note: There is an alternate definition of height as the number of edges traversed. In that case, the height of a leaf would be 0.) |
| Depth | The length of the path from the node to the root. The depth of the root node is 0. |
Sometimes we’ll refer to the height and depth of a tree as a whole. In these cases, it’s usually assumed that we’re referring to the height of the root node and the depth of the deepest leaf, respectively.
Definition
For a linked structure of nodes to be considered a tree:
- nodes must have no parents or 1 parent
- there can be no cycles (paths that start and end at the same node)
- there can only be one path between any two nodes in a tree
- all nodes must be a descendant of the root (except the root itself)
Discussion: Examples of Trees
Discuss with your partner whether the following examples would be considered trees as we’ve introduced them above.
- Linked List
- Family Tree
Trees are naturally recursive structures, so you’ll find that we implement a lot the methods in this lab using recursion because it tends to be the simplest solution.
Amoeba Family Tree
An amoeba family tree is an example of our above definition of a tree. It is simpler than a normal family tree because amoebas do not need partners in order to reproduce. An amoeba has one parent, zero or more siblings, and zero or more children. An amoeba also has a name.
Below is the skeleton code for an Amoeba. The full code is located in the AmoebaFamily.java file. Below, we are seeing the ArrayList for the first time. It is quite similar to the ArrayDeque you made! Take a look at the API for more information on its methods and usage.
class Amoeba {
public String name;
public Amoeba parent;
public ArrayList<Amoeba> children;
}
And below is a box and pointer diagram of our Amoeba.
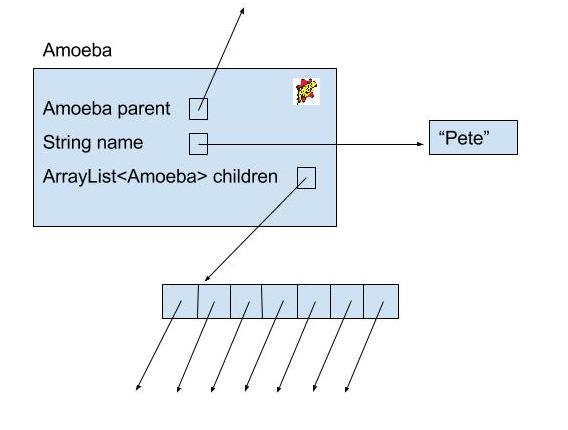
Amoebas (or amoebae) live dull lives. All they do is reproduce, so all we need to keep track of them are the following methods:
/* Creates an AmoebaFamily, where the first Amoeba's name is NAME. */
public AmoebaFamily(String name) {
root = new Amoeba(name, null);
}
/* Adds a new Amoeba with childName to this AmoebaFamily as the youngest
child of the Amoeba named parentName. This AmoebaFamily must contain an
Amoeba named parentName. */
public void addChild(String parentName, String childName) {
if (root != null) {
root.addChildHelper(parentName, childName);
}
}
The Amoeba objects are the nodes of our tree, represented by the AmoebaFamily object. You will find that most of the methods of this AmoebaFamily will be implemented through recursive helper methods of the Amoeba class.
Void Recursive Methods
In the AmoebaFamily class, we provide the method addChild to add a new Amoeba to the AmoebaFamily tree. The method implements a general traversal of the tree using a void recursive method in the Amoeba class. You will now implement another void recursive method, print, and your goal is to make the solution to this method as similar as possible to addChild.
Exercise: print
This print method should print the root Amoeba’s name and the names of all its descendants. One name should be printed per line. The names of the children of each descendant Amoeba should be printed on the lines immediately following. Each name should be indented four spaces more than the name of their parent Amoeba. Thus, the output should appear in the following form:
amoebaName
childName
grandchildName
greatGrandchildName
greatGreatGrandchildName
grandchildName
childName
grandchildName
childName
childName
grandchildName
We have included an example AmoebaFamily in the tester file AmoebaFamilyTest.java, so when you call print on that AmoebaFamily, you should receive the following output if implemented correctly:
Amos McCoy
mom/dad
me
Mike
Bart
Lisa
Homer
Marge
Bill
Hilary
Fred
Wilma
auntie
You will likely need a helper method whose argument keeps track of the indenting level, but the form should still be similar to addChild!
Non-void Recursive Methods
So far, the methods we’ve seen for the AmoebaFamily class have not returned anything; they have only been modifying the state of the AmoebaFamily. We will be able to do cooler things if we can return values, and the next example will take advantage of this.
Exercise: longestName
Implement the longestName method in the AmoebaFamily class. Make this as similar to longestNameLength as possible. You will find that these non-void recursive methods follow a specific pattern, one that you will likely draw upon again when solving problems that you face in the future.
You will not need to use longestNameLength directly in your implementation of longestName.
Binary Trees
We’ll now move on from trees and explore a common, special case of the tree data structure: the binary tree. A binary tree is a tree in which each node has at most two children. Rather than store the children in an ArrayList as was done in Amoeba nodes, one normally just has two separate variables left and right for the left and right children of the binary tree.
Exercise: BinaryTree
The file BinaryTree.java defines a BinaryTree class and a TreeNode class. First, read over the code and then implement the following three methods.
Note: See BinaryTreeTest.java for the same sample trees that the autograder uses, and write your own tests there to verify correctness.
Exercise 1: height
First, switch which partner is coding if you haven’t recently.
Add a height method to the BinaryTree class. The height of an empty tree is 0; the height of a one-node tree is 1; the height of any other tree is 1 + the greater of the heights of the two children.
Exercise 2: isCompletelyBalanced
Add an isCompletelyBalanced method for the BinaryTree class. A tree with no nodes and a tree with one node are both completely balanced; any other tree is completely balanced if and only if the height of its left child is equal to the height of its right child, and its left and right children are also completely balanced. Make sure you test your code with trees of height 3 or more to ensure that your code works!
Exercise 3: fibTree
This exercise deals with “Fibonacci trees”, trees that represents the recursive call structure of the Fibonacci computation. (The Fibonacci sequence is defined as follows: \(F_0 = 0, F_1 = 1\), and each subsequent number in the sequence is the sum of the previous two.) The root of a Fibonacci tree should contain the value of the Nth Fibonacci number, the left subtree should be the tree representing the computation of the N-1th Fibonacci number, and the right subtree should be the tree representing the computation of the N-2th Fibonacci number. The two exceptions to this rule are when we pass in 0 or 1 to the fibTree method. The first few Fibonacci trees appear below.
| Function | Tree |
|---|---|
fibtree(0) |  |
fibtree(1) |  |
fibtree(2) | 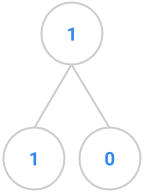 |
fibtree(3) | 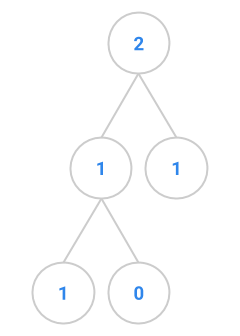 |
fibtree(4) | 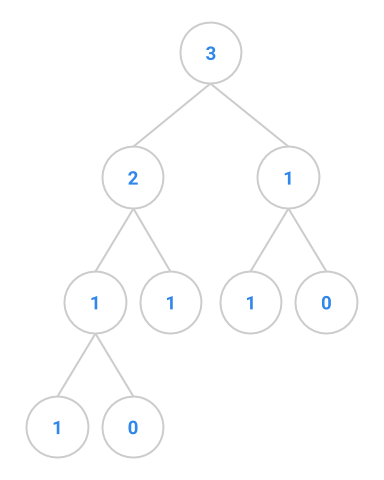 |
fibtree(5) | 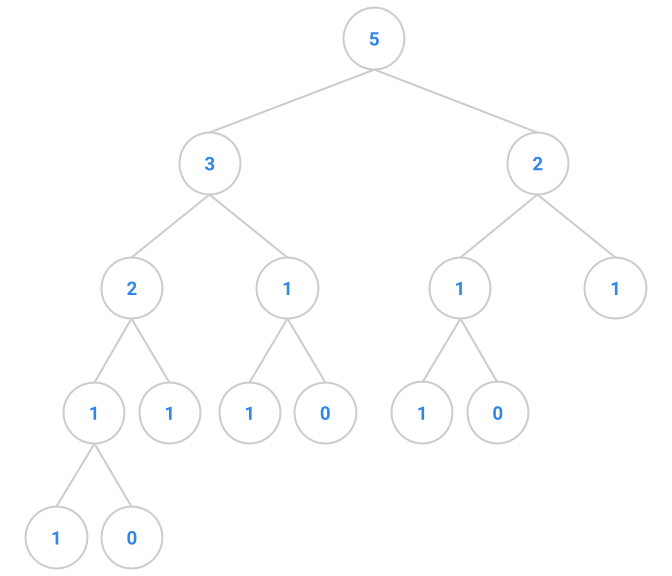 |
Supply the static fibTree method in BinaryTree that takes in a non-negative integer N, and returns a BinaryTree that stores the N-th Fibonacci value using the representation above.
Remember how we’ve been delegating structuring all our methods so far for the best code!
Conclusion
Readings
We will soon go into binary search trees in more depth. You may find Shewchuk’s notes on Binary Search Trees helpful.
Deliverables
To finish this lab, make sure to finish the following and submit to Gradescope:
- Complete the following methods in
AmoebaFamily:print()longestName()
- Complete the following methods in
BinaryTree:height()isCompletelyBalanced()fibTree()
There is no worksheet for this lab. The coding submission will be worth the full 3 points for today.
