The worksheet today will be worth 1.5 points and the code submission will be worth 1.5 points.
Introduction
Making Your Shared Partner Repository
Please do not skip this section. Partnerships are required and you must complete your work in the shared repository. See the Collaboration Guide for more information.
Today, you should be working with the partner you intend to collaborate with for project 2. Starting today, you two will be required to work together through the due date of the project on both the labs and the project. If you are looking for a partner, please let your TA know; they’d love to help!
The two of you will be working from a shared repository. Please go to the Partnerships page on Beacon, and invite your Project 2 partner (Only one partner needs to do this!). Generate the magic link and have your partner click on it to confirm.
Once confirmed, your partnership page on beacon will contain a link to view the repository on GitHub, which should have a name of the form su19-proj2-s***-s***.
Both of you should clone this repository. Make sure you do not clone this repository inside of another repository–you will experience git problems if you do so.
$ git clone https://github.com/Berkeley-CS61B-Student/su19-proj2-s***-s***.git
Change directory into it:
$ cd su19-proj2-s***-s***
And add the skeleton remote:
$ git remote add skeleton https://github.com/cs61bl/skeleton-su19.git
You’ll then be able to pull as usual:
$ git pull skeleton master
If you get an error similar to “fatal: refusing to merge unrelated histories”, you can fix this by, for this time only, running:
$ git pull --rebase --allow-unrelated-histories skeleton master
You should be using this shared repository for this week’s labs and the project. Both you and your partner will work together on the same code base. After adding and commiting your own work, you can receive your partner’s work:
$ git pull origin master
Overview
Yesterday we looked at Trees and Binary Trees, trees in which each node can have no more than two children. Today we will explore ways of traversing these trees; ways in which we can examine or process each node in the data structure. Note that unlike a linear structure such as a linked list, which can only be traversed from front to back (or back to front), with trees there are many more orderings in which we can explore its contents.
We know that anytime we want to do something over and over again (in this case, visit the “next” node over and over again until we are done), we have two approaches we can use: recursion and iteration. Let’s start by looking at recursive strategies first.
Recursive Traversals
If we were to write recursive pseudocode to visit every node, it would probably look something like this:
// This is pseudocode.
binaryTreeTraversal(node):
if left != null:
binaryTreeTraversal(left)
if right != null:
binaryTreeTraversal(right)
Visiting each node allows us to get to node instance, but when we get to a node, we aren’t doing anything. (Why go to Napa if you’re not going to taste some fine wines?)

If I wanted to process the nodes in some way (such as by printing its value, destructively squaring its value, etc.), there are three places I can do that in this recursive traversal code. I can put my print line, for example, either:
binaryTreeTraversal(node):
// HERE
if left != null:
binaryTreeTraversal(left)
// HERE
if right != null:
binaryTreeTraversal(right)
// OR HERE
It turns out, processing at those three different locations yields different orders in which the nodes are processed. Thus, we give each of these locations a special name:
- Pre-order means to process the current node before pre-order traversing down the left and right of the current node.
- In-order means to first in-order traverse the left of the current node, process the current node, and then in-order traverse down the right of the current node.
- Post-order means to post-order traverse down the left and right of the current node before finally processing the current node.
Thus we have,
binaryTreeTraversal(node):
preorder(node)
if left != null:
binaryTreeTraversal(left)
inorder(node)
if right != null:
binaryTreeTraversal(right)
postorder(node)
Worksheet: 1. Recursive Traversals
Complete this exercise on your worksheet.
Visual Trick
Visually, you can determine the order nodes are processed during pre-, in-, or post-order traversal by drawing a peg on the west, south, or east side of each node, respectively, and tracing a line around the tree diagram as shown below. The nodes are processed in the order the yellow line touches each red peg.
Pre-order has pegs on the west side of each node. A, B, C, D, E. 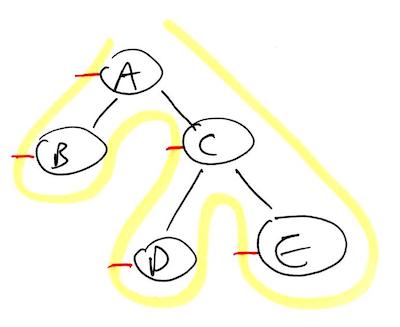
In-order has pegs on the south side of each node. B, A, D, C, E. 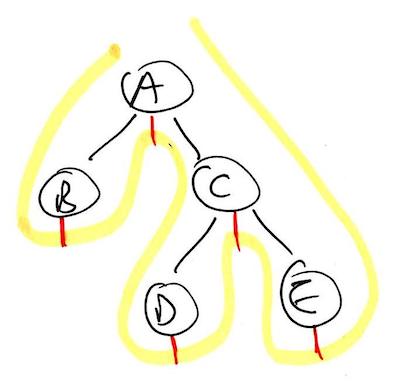
Post-order has pegs on the east side of each node. B, D, E, C, A. 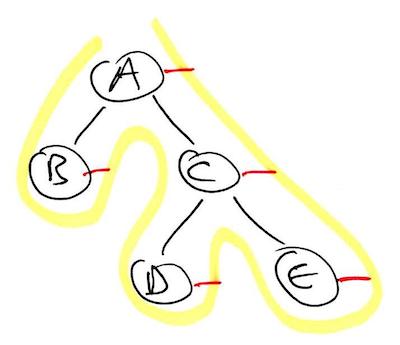
This trick always works because it is a literal translation of what the pseudocode is doing. For example, pre-order is defined as processing the current node before going to the left and right children, and so here in our picture, we ensure the line we are tracing runs into the peg, which we’ve placed on the west side of the node, before it ventures around to the left and right children of the node. As for the reasoning behind the traced line itself, well that is the natural order in which the nodes are visited when the code is run recursively.
Go back to question 1 and verify that the answers you’ve derived from the code match what you get if you just read off the traversals visually.
Out of pre-order, in-order, post-order, which of these definitions would make sense being extended to trees with more than just two children?
Answer: Only pre-order and post-order. We can process either before or after visiting all of the children, but the definition of in-order relies on processing between the left and right child visit; if there are more than two children, the time at which this process operation should be performed isn’t really clear anymore.
Exercise: Recursive Traversals
Using the pseudocode provided above, implement preorder(), inorder() and postorder() in BinaryTree.java (this file is similar to that from the previous lab). You will probably want to create helper functions to help you track the current node.
Print the items on a single line, separated with a space. System.out.print(n.item + " ").
If root == null your traversal functions should print nothing and terminate without encountering any errors (i.e. this case should not cause a NullPointerException).
In BinaryTreeTest.java you have a test which loads up worksheetTree(), which is the same tree shown on the worksheet. Modify the test to ensure your three functions print a list containing the same numbers you determined in worksheet question 1.
Stacks and Queues
Before we go into the iterative traversals, we will go over two new data structures that will help us.
Recall that your Deque data structures from Project 1 allowed for adding and removing from both the front and the back (first and last). However sometimes that is too powerful and we do not need all of that functionality. Thus, we will introduce the stack and the queue data structures, which are similar, but have more limited, precise functionality.
A stack models a stack of papers, or plates in a restaurant, or boxes in a garage or closet. A new item is placed on the top of the stack, and only the top item on the stack can be accessed at any particular time. Stack operations include the following:
- pushing an item onto the stack
- popping the top item off the stack
- peeking/accessing the top item of the stack (but not removing it)
- checking if the stack is empty.
As a result, we often refer to stacks as processing in LIFO (last-in, first-out) ordering; the first pancake to come off griddle will land on the plate first but will be the last pancake to be eaten since I must eat the fresh pancakes on the top of the stack before I can eat the earlier-cooked ones which are sitting lower in the stack. Essentially, this is like only allowing addFirst() and removeFirst() operations, except we call them push() and pop() instead.

A queue is a waiting line. As with stacks, access to a queue’s elements is restricted. Queue operations include:
- enqueueing/adding/offering an item to the back of the queue
- dequeueing/polling the item at the front off of the queue
- peeking at the front item (but not removing it)
- checking if the queue is empty
As a result, we often refer to queues as processing in FIFO (first-in, first-out) ordering; the first person to jump in line for fish and chips at the marina will be served first, and as new people jump in line, they must wait until everyone before them has been served before they have a chance to enjoy light, flaky fish steaks paired with luscious tarter sauce and a generous side of fries. Essentially, this is like only allowing addLast() and removeFirst() operations, except we call them offer() and poll().

Worksheet: 2. Stacks and Queues
Complete this exercise on your worksheet.
Iterative Traversals
When we traverse an array we need an index/counter variable and when we traverse a LinkedList we need a node pointer. For tree traversal, we can use certain data structures to help us keep track of where we are. This is called a fringe.
Here is our pseudocode for iteratively traversing through a tree (do you see the similarities it has with a linked list iterative traversal?)
// This is pseudocode.
Use a STACK as the fringe.
Add root to fringe.
while fringe not empty:
Remove next from fringe.
Add its children to fringe.
Process removed node.
This particular traversal is called DFS or Depth First Search Traversal.
Similarly, we can make a small change to end up with what is called BFS or Breadth First Search Traversal:
Use a QUEUE as the fringe.
Add root to fringe.
while fringe not empty:
Remove next from fringe.
Add its children to fringe.
Process removed node.
Worksheet: 3. Iterative Traversals
Complete this exercise on your worksheet.
You may notice that the directions tell to add the children in a specific order for each traversal. How does doing so ensure that we examine the left side of the tree first for both traversals? (We like to do these on-paper problems by breaking ties from left to right, but in code, technically both ways of breaking such a tie are valid.)
Exercise: Iterative Traversals
Using the pseudocode provided above, implement dfs() and bfs() in BinaryTree.java. You may want to use Java’s LinkedList implementation for your fringe, since its functions can make it behave as either a stack or a queue (Java’s LinkedList implements the Java Deque interface).
Print the items on a single line, separated with a space. System.out.print(n.item + " ").
If root == null your traversal functions should print nothing and terminate without encountering any errors (i.e. this case should not cause a NullPointerException).
Again, use BinaryTreeTest.java and the worksheetTree() to test your implementations against the results you determined in question 3.
Worksheet: 4. Follow-up Questions
Complete this exercise on your worksheet.
Exercise: Sum Paths
Define a root-to-leaf path as a sequence of nodes from the root of a tree to one of its leaves. Complete the method printSumPaths(int k) in BinaryTree.java that prints out all root-to-leaf paths whose values sum to k.
For example, for the binary tree rooted in 10 in the diagram below, if k is 13, then the program will print out 10 2 1 on one line and 10 4 -1 on another.
10
/ \
2 4
/ \ \
5 1 -1
You may assume that this function will only be called when the generic T is Integer.
If root == null your function should print nothing and terminate without encountering any errors (i.e. this case should not cause a NullPointerException).
Use BinaryTreeTest.java to write tests.
Conclusion
Readings
The next lab will cover binary search trees. You may find Shewchuk’s notes on Binary Search Trees helpful.
Deliverables
Fill in the methods in BinaryTree.java:
preorderinorderpostorderdfsbfsprintSumPaths
Submit the worksheet to your lab TA by the end of your section.