The worksheet today will be worth 1 point, the weekly survey will be worth 0.5 points, and the code submission will be worth 1.5 points.

Before You Begin

As usual, pull the skeleton code.

Learning Goals

In this lab, you’ll learn about two fundamental parts of comparing objects, the .equals() method for equality, and the Comparator and .compareTo() method for ordering. Both techniques will be widely used in the remainder of the class.

Comparison

Read Chapter 4.3 from Max Function through Comparables to help motivate the problem we’re solving and the tools we’ll use along the way.

While we haven’t explicitly learned about sorting yet, the idea of sorting should be intuitive enough. You have a list of things, and you want to put it in sorted order. While this makes sense immediately for things like ints, which we can compare with primitive operations like < and ==, this becomes less clear for general objects.

Take a look at the Java API for the Comparable<T> interface. A lot of things implement Comparable in the Java standard library, as comparing two of the same type of object is a very common idea.

The only method required by Comparable is compareTo(T o) which takes another object of the (same) type T and returns an int whose value represents whether this or o should come first. In order to sort a list in Java, most sorting algorithms will call compareTo and make pairwise comparisons to determine which object should come first, repeatedly, and swap elements until the entire list is sorted. (The thing that makes sorting interesting, then, is determining which compareTo ‘questions’ (and how many) will be necessary in order to achieve proper ordering).

Here are a few key details from compareTo, slightly adapted:

Compares this object with the specified object for order. Returns a negative integer, zero, or a positive integer if this object is less than, equal to, or greater than the specified object, respectively.

There are other requirements that usually just happen naturally with a reasonable implementation, but are still important to specify:

The implementor must also ensure that the relation is transitive: (x.compareTo(y) > 0 && y.compareTo(z) > 0) implies x.compareTo(z) > 0.

It is strongly recommended, but not strictly required that x.compareTo(y) == 0 is equivalent to x.equals(y). Generally speaking, any class that implements the Comparable interface and violates this condition should clearly indicate this fact. The recommended language is “Note: this class has a natural ordering that is inconsistent with equals.”

Typically, a class will compare to objects of the same type as itself (although it does not strictly have to). Doing so means data structures that require ordering (like sorted lists, and in the future, search trees) can contain the class.

Exercise: User

In User.java, we’ve provided an example of how a website might model a user.

Make User implement Comparable. Use the generic parameter to Comparable to ensure that User can only be used to compare against other Users.

The natural ordering for User is to compare by ID number. If their ID numbers are the same, then compare them on their username.

After implementing this, you should be able to sort Users:

public static void main(String[] args) {
    User[] users = {
        new User(3, "Christine", ""),
        new User(4, "Matt", ""),
        new User(-1, "Alex", ""),
        new User(2, "Lauren", ""),
        new User(2, "Itai", "")
    };
    Arrays.sort(users);
    for (User user : users) {
        System.out.println(user);
    }
}

User{id=-1, name=Alex, email=}
User{id=2, name=Itai, email=}
User{id=2, name=Lauren, email=}
User{id=3, name=Christine, email=}
User{id=4, name=Matt, email=}

Note that here we use Arrays.sort because users is an array; if it was a Java Collection like ArrayList, we would use Collections.sort.

Higher-Order Functions

Then, read about Higher-Order Functions, the topic we’ll be exploring and building upon for the next portion of the lab.

A higher-order function is a function that treats other functions as data. In the textbook, we saw that we could create higher-order functions with the help of inheritance by defining additional classes to represent each operation.

public interface IntUnaryFunction {
    int apply(int x);
}

public class TenX implements IntUnaryFunction {
    /* Returns ten times the argument. */
    public int apply(int x) {
        return 10 * x;
    }
}

By defining the IntUnaryFunction interface, the Java compiler is able to type check and ensure that all parts of the program are safe to run.

There are some significant downsides to this design. For every function you want to use, you have to define a new class, along with writing all super-interfaces for the whole hierarchy. One shortcut you can take is defining anonymous classes, a common pattern used in programming for the Android OS, but one we will not explore in this course. Instead, we’ll take a look at a few other recent Java features like lambdas, which reduce the amount of code we need to write by having the compiler do as much as it can to infer the relationship between TenX and IntUnaryFunction.

Comparators

A Comparator<T> is an example of a Java higher-order function for imposing ordering on objects (if they have no natural ordering), and/or overriding their natural ordering as specified by Comparable.

Read Comparator in Chapter 4.3 of the online textbook.

Comparator only requires one method to be implemented: compare(T o1, T o2), which “Returns a negative integer, zero, or a positive integer as the first argument is less than, equal to, or greater than the second.” It should behave transitively & symmetrically, and returning zero should also imply that o1.equals(o2).

Then, we can pass in the Comparator object as the second argument to Arrays.sort (the same works for Collections.sort) and sort on whatever we want. For example, if we wanted to sort integers in reverse order, we can create a ReverseComparator and reverse the result usual Integer comparison.

public class ReverseComparator implements Comparator<Integer> {

    public Integer compare(Integer o1, Integer o2) {
        return -(Integer.compare(o1, o2));
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3};
        Arrays.sort(arr, new ReverseComparator());
        // The above line sorts based on ReverseComparator's compare method
        System.out.println(Arrays.toString(arr)); // [3, 2, 1]
    }
}

Function Interface

The Java standard library now includes a Function interface, a standard interface for any programmer to pass around function objects. Instead of having to use our own made-up interface, we can implement interfaces from Java’s universal Function hierarchy.

Now, when it comes to writing things like Comparators, it means we no longer have to write a custom class. This is because a Comparator is a functional interface (that is, it only has one abstract method that must be implemented) and can be replaced by any appropriate lambda function or method reference.

Now we can use Arrays.sort like a true higher order function. Let’s revisit the example of sorting integers in reverse order.

Here are two ways to do it.

Using a method reference

public class IntSorter {
    public static int reverseCompare(Integer i1, Integer i2) {
        return -(Integer.compare(i1, i2));
    }

    public static void main(String[] args) {
        int[] arr = {1, 2, 3};
        Arrays.sort(arr, IntSorter::reverseCompare);
        System.out.println(Arrays.toString(arr)); // [3, 2, 1]
    }
}

The :: notation denotes the reverseCompare method of the IntSorter class. You can also do this for instance methods (without associating it with an object) or with the instance method of a particular object (like instance::method). This is the equivalent of passing the method around by reference.

Note some of the differences between this and the previous Comparator example. Here, we pass in a method reference. IntSorter does not implement the Comparator interface, and we never make a new instance of IntSorter

Using a lambda expression

public static void main(String[] args) {
    Integer[] arr = {1, 2, 3};
    Arrays.sort(arr, (o1, o2) -> -(Integer.compare(o1, o2)));
    System.out.println(Arrays.toString(arr)); // [3, 2, 1]
}

Notice the syntax here. First, the arguments to the method are declared, then an arrow, followed by the return value. The typed parameters are not provided, and the compiler will infer them automatically by their use. Of course, longer and more specific lambda statements are possible, using multiple statements and return statements, and using typed parameters, like so:

Arrays.sort(arr, (Integer o1, Integer o2) -> {
            System.out.println("Do more stuff here");
            return -(Integer.compare(o1, o2));
        });

Worksheet: 1. Comparators

Complete this exercise on your worksheet.

Exercise: getOrderedBy

Take a look at DBTable.java. It is a simple thin wrapper around a List<T>. You will be adding functionality for a few common operations on a list of things like what we find in databases. In our example, T will always be a User, but your code should generalize to any type.

Implement getOrderedBy.

public <R extends Comparable<R>> List<T> getOrderedBy(Function<T, R> getter)

The <R extends Comparable<R>> is a method generic, which declares a generic type local to a single method (rather than the entire class), and can be used throughout the method similar to generics in classes. The method generic goes after the visibility keyword, public, and before the return type declaration, List<T>. Additionally, there is a bound on the generic type R, stating that only types that extend Comparable<R> will be accepted by the compiler.

getOrderedBy should take in a method reference to a getter method of the T class, and return a new List<T>, ordered on the return value of that getter method. Example usage:

public static void main(String[] args) {
    List<User> users = Arrays.asList(
        	new User(3, "Christine", ""),
       		new User(4, "Matt", ""),
        	new User(-1, "Alex", ""),
        	new User(2, "Lauren", ""),
        	new User(2, "Itai", "")
            );
    DBTable<User> t = new DBTable<>(users);
    List<User> l = t.getOrderedBy(User::getName);
    l.forEach(System.out::println);
}

User{id=-1, name=Alex, email=}
User{id=3, name=Christine, email=}
User{id=2, name=Itai, email=}
User{id=2, name=Lauren, email=}
User{id=4, name=Matt, email=}

Like before, the Function interface only requires a single method be implemented, R apply(T t), which represents the behavior of the Function itself. Functions also have other methods, which are marked default, that can do other cool features, like composing functions with the compose method, similar to currying in CS 61A, and chaining functions through andThen.

Implement getOrderedBy according to specification. You will need to make usage of a custom comparator, without writing Comparator once.

Hint: Use a lambda statement. Do not mutate DBTable’s entries.

Recap

A max Function

Suppose we want to write a function max() that returns the max of any array regardless of type. If we write a method max(Object[] items), where we use the ‘>’ operator to compare each element in the array, this will not work! Why is this the case?

Well, this makes the assumption that all objects can be compared. But some objects cannot! Alternatively, we could write a max() function inside the Dog class, but now we have to write a max() function for each class that we want to compare! Remember, our goal is to write a “one true max method” that works for all comparable objects.

OurComparable Interface

The solution is to create an interface that contains a compareTo(Object) method; let’s call this interface OurComparable. Now, our max() method can take a OurComparable[] parameter, and since we guarantee that any object which extends the interface has all the methods inside the interface, we guarantee that we will always be able to call a compareTo method, and that this method will correctly return some ordering of the objects.

Now, we can specify a “one true max method”. Of course, any object that needs to be compared must implement the compareTo method. However, instead of re-implementing the max logic in every class, we only need to implement the logic for picking the ordering of the objects, given two objects.

Comparable Interface

Java has an in-built Comparable interface that uses generics to avoid any weird casting issues. Plus, Comparable already works for things like Integer, Character, and String; moreover, these objects have already implemented a max, min, etc. method for you. Thus you do not need to re-do work that’s already been done!

Comparator Interface

The term “Natural Order” is used to refer to the ordering implied by a Comparable’s compareTo method. However, what if we want to order our Dog objects by something other than size? We will instead pass in a Comparator<T> interface, which demands a compare() method. We can then implement the compare() method anyway we want to achieve our ordering.

Worksheet: 2. Collections

Complete this exercise on your worksheet.

Binary Search

In the last question above, we achieve an improved runtime by employing the well known divide-and-conquer algorithm known as binary search. Used with an array where low, mid, and high are array indices, it assumes that the elements of the array are in increasing order, and executes the following:

1. Set low to 0 and high to the length of the array minus 1. The value we’re looking for — we’ll call it k— will be somewhere between position low and position high if it’s in the array.
2. While low \(\leq\) high, do one of the following:
   • Compute mid, the middle of the range [low, high], and see if that’s k. If so, return mid.
   • Otherwise, we can cut the range of possible positions for k in half, by setting high to mid - 1 or by setting low to mid + 1, depending on the result of the comparison.
3. If the loop terminates with low > high, we know that k is not in the array, so we return some indication of failure.

The diagrams below portray a search if k was equal to 25. Elements removed from consideration at each iteration are greyed out.

low = 0, high = 14, mid = 7

low = 0, high = 6, mid = 3

low = 4, high = 6, mid = 5

low = 4, high = 4, mid = 4

Since (roughly) half the elements are removed from consideration at each step, the worst-case running time is proportional to \(\log_2 N\), where \(N\) is the number of elements in the array.

Worksheet: 3. Binary Search

Complete this exercise on your worksheet.

Binary Search Trees

The binary search algorithm suggests a way to organize keys in an explicitly linked tree, as indicated in the diagram below.

The data structure that results is called a binary search tree (BST). Given that the root value (one of the keys to be stored) is \(k\), a binary search tree is organized as follows:

• Put all the keys that are smaller than \(k\) into a binary search tree, and let that tree be \(k\)’s left subtree.
• Put all the keys that are larger than \(k\) into a binary search tree, and let that tree be \(k\)’s right subtree.

This organization assumes that there are no duplicate keys among those to be stored.

Worksheet: 4. BST Identification

Complete this exercise on your worksheet.

contains

It’s important to note that in a binary search tree, each subtree is also a binary search tree. This suggests a recursive or iterative approach for implementing many methods, and the contains method is no different. In pseudocode, here is an outline of the helper method of the contains method, containsHelper(TreeNode t, T key):

1. An empty tree cannot contain anything, so if t is null return false.
2. If key is equal to t.item, return true.
3. If key < t.item, key must be in the left subtree if it’s in the structure at all, so return the result of searching for it in the left subtree.
4. Otherwise it must be in the right subtree, so return the result of searching for key in the right subtree.

Note: that the type of key is T, which is the generic type of the BinaryTree class.

This algorithm can go all the way down to a leaf to determine its answer. Thus in the worst case, the number of comparisons is proportional to \(d\), the depth of the tree. In a balanced tree (more on that next lab), you can expect the depth of the tree to be proportional to \(\log N\) in the worst case, where \(N\) is the number of nodes in the tree.

Use of Comparable objects

Finding a value in the tree will require “less than”, “greater than”, and “equals” comparisons. Since the operators < and > don’t work with objects, we have to use method calls for comparisons.

The Java convention for this situation is to have the values stored in the tree be objects that implement the Comparable interface. This interface prescribes just one method, int compareTo (Object). For Comparable objects obj1 and obj2, obj1.compareTo (obj2) returns

• negative if obj1 is less than obj2,
• positive if obj1 is greater than obj2, and
• zero if the two objects have equal values.

Balance and Imbalance

Unfortunately, use of a binary search tree does not guarantee efficient search. For example, the tree

is a binary search tree in which search proceeds in the same runtime as a linked list. We thus are forced to consider the balance of a binary search tree. Informally, a balanced tree has subtrees that are roughly equal in size and depth. Next lab, we will encounter specific algorithms for maintaining balance in a binary search tree. Until then, we will work under the possibly unwarranted assumption that we don’t need to worry much about balance.

One can prove (optional to read, but an important fact to know), incidentally, that search in a BST of \(N\) keys will require only about \(2 \ln N\) comparisons (where \(\ln\) is the “natural log” of \(N\)) if the keys are inserted in random order. Well-balanced trees are common, and degenerate trees are rare.

Insertion into a BST

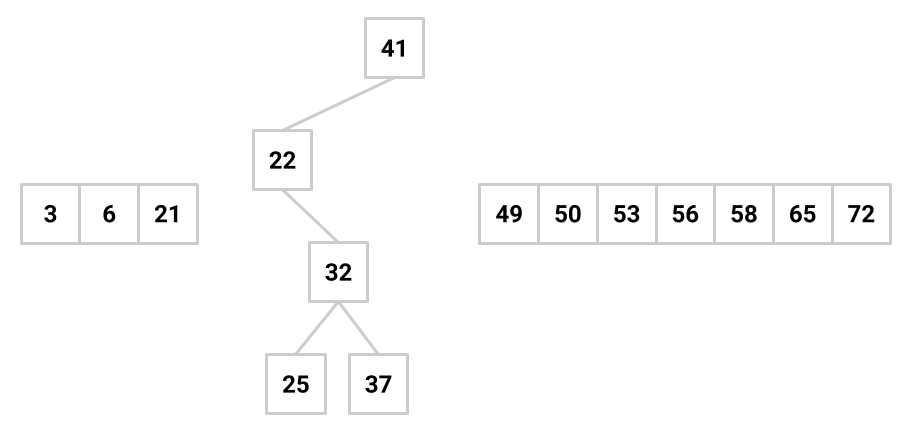
If we have 4 nodes in our binary search tree, there are actually 14 different BST’s you could make. Correspondingly, there are typically a bunch of places in a BST that a key to be inserted might go, anywhere from the root down to a leaf. Given below are two trees; the tree on the right shows one possible way to insert the key 41 into the tree on the left.

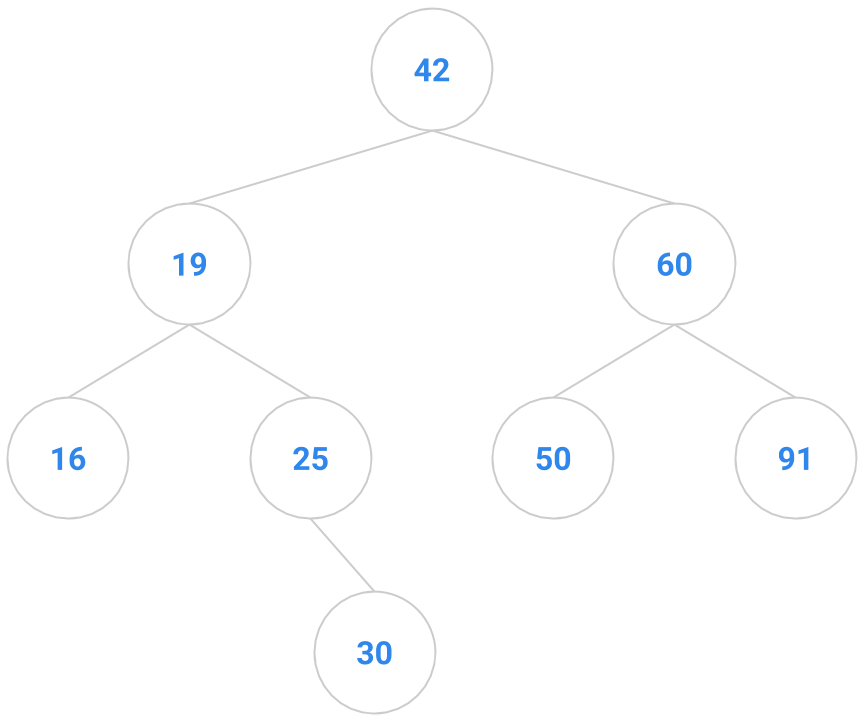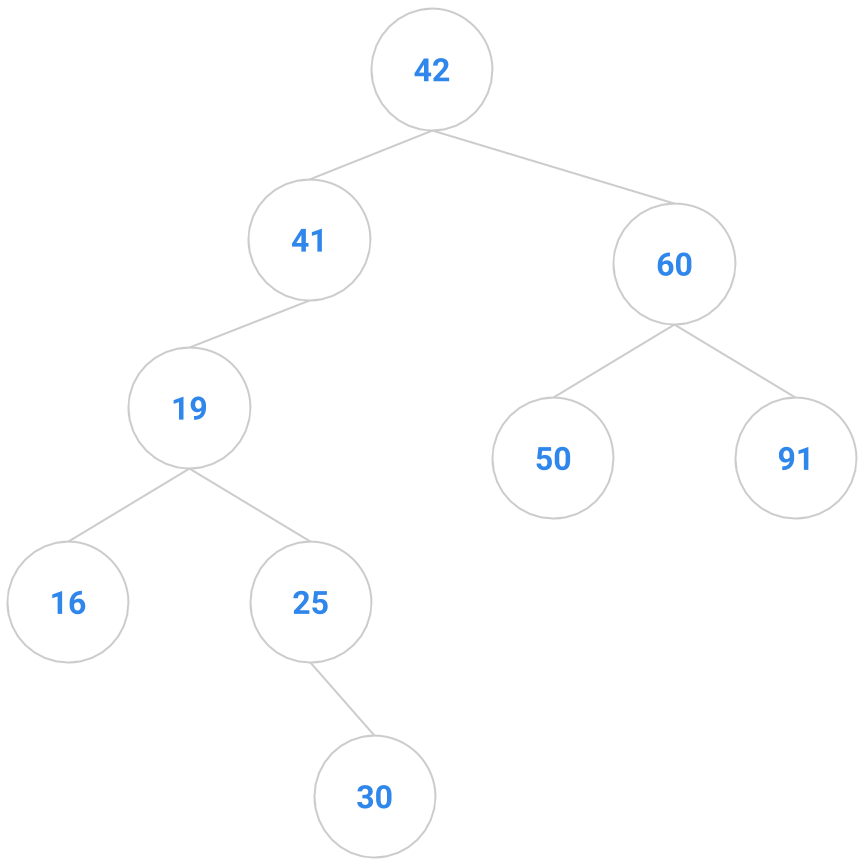However, to minimize restructuring of the tree and the creation of internal nodes, we choose in the following exercise to insert a new key only as a new leaf.

USFCA put together a BST visualization interactive animation to help you visualize the BST insertion and deletion algorithms. Try inserting a key that ends up as a right child and another key that ends up as a left child. Add some more nodes to the tree, then delete some of them: a node with no children, a node with one child, and a node with two children.

Note that this animation removes from the BST by swapping with the inorder predecessor rather than the inorder successor. Convince yourself this is essentially equivalent.

Exercise: BST Implementation

Now it’s time to start writing code! As you go, don’t forget to write JUnit tests.

Since binary search trees share many of the characteristics of regular binary trees, we can define the BinarySearchTree class using inheritance from a provided BinaryTree class.

Exercise 1: Implement Constructors

The BinarySearchTree class is defined as follows:

public class BinarySearchTree<T extends Comparable<T>> extends BinaryTree<T>

This class definition is a slightly more complicated use of generic types than you have seen before in lab. Previously, you saw things like BinaryTree<T>, which meant that the BinaryTree class had a generic type T that could be any class, interface, or abstract class that extends Object. In this case, BinarySearchTree<T extends Comparable<T>> means that the BinarySearchTree class has a generic type T that can be any class, interface, or abstract class that implements the Comparable<T> interface. In this case, Comparable<T> is used because the Comparable interface itself uses generic types (much like the Iterable and Iterator interfaces).

Take a look through the BinarySearchTree and BinaryTree classes, and familiarize yourself with the methods that are available to you. Then, implement the two constructors for the BinarySearchTree class, using only method calls to super.

Exercise 2: contains

Now, we will implement the contains method. We will use the following method signature:

public boolean contains(T key)

which takes a Comparable object T as an argument and checks whether the tree contains it.

Recall that Comparable objects provide an int compareTo method that returns:

• a negative integer if this object is less than the argument,
• a positive integer if this object is greater than the argument, and
• 0 if the two objects have equal values.

Depending on whether you take a recursive or iterative approach, you may need to define a helper method. If you’re stuck, take a look at the pseudocode that we described above!

Exercise 3: add

We will now define an add method. We will use the following method signature:

public void add(T key)

which takes a Comparable object as an argument and adds it to the tree if and only if it isn’t already there. The trees you create with the add method will thus not contain any duplicate elements.

Hint: You should be able to do this in a similar way to the contains method. When you’re done with both, you can write a JUnit test suite to test your code. Don’t forget edge cases!

Worksheet: 5. Comparison Counting

Complete this exercise on your worksheet.

Worksheet: 6. Binary Search Trees

Complete this exercise on your worksheet.

Discussion: BST Deletion

We’ve covered adding to a BST and contains in a BST. But how about deletion?

When inserting a key, we were allowed to choose where in the tree it should go. The deletion operation doesn’t appear to allow us that flexibility; deletion of some keys will be easy (leaves or keys with only one child), but our deletion method has to be able to delete any key from the tree.

Here are a bunch of binary search trees that might result from deleting the root of the tree

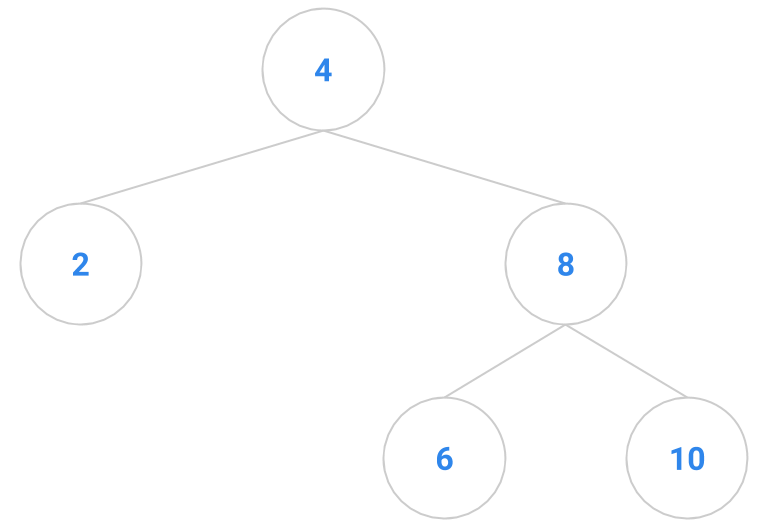
Which ones do you think are reasonable?

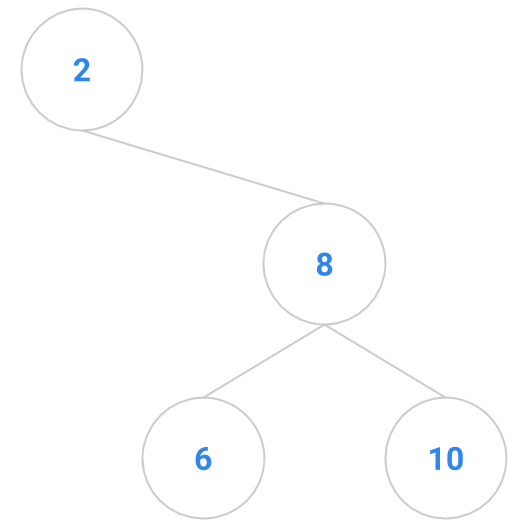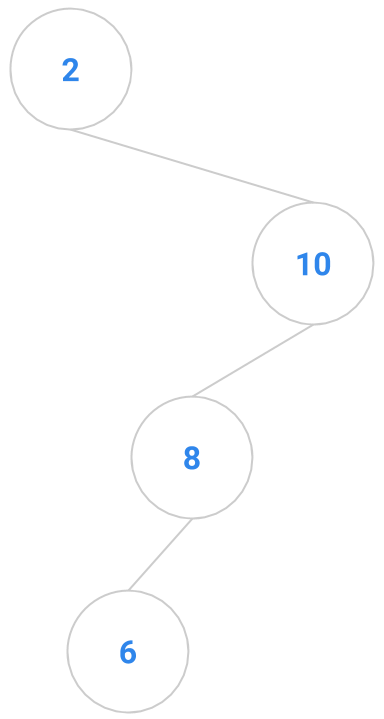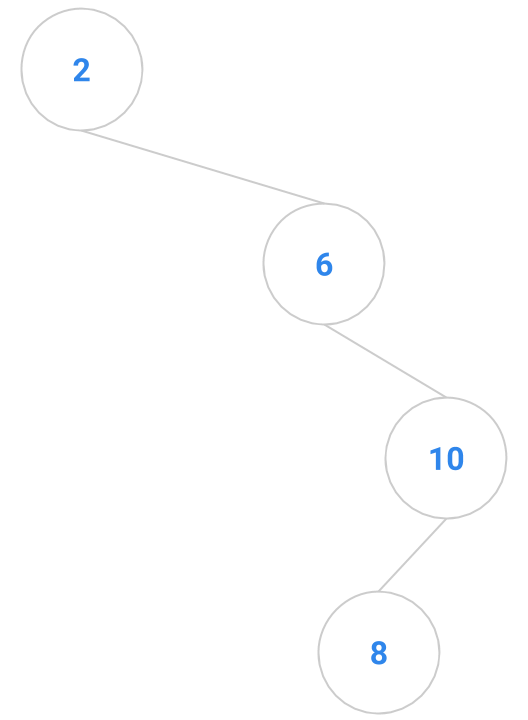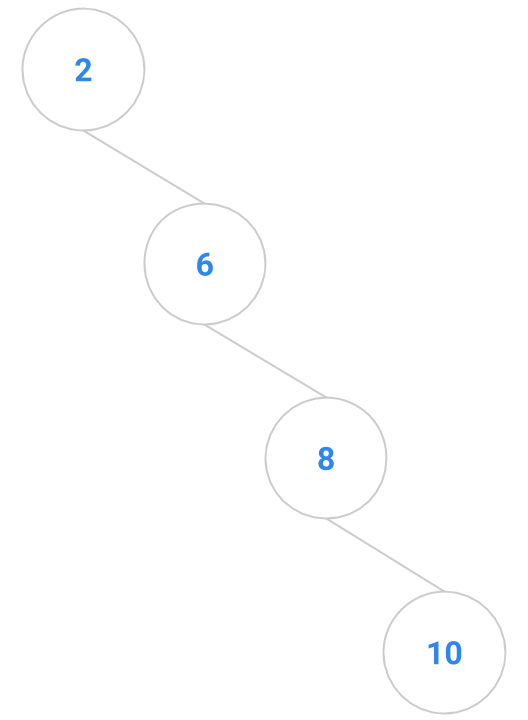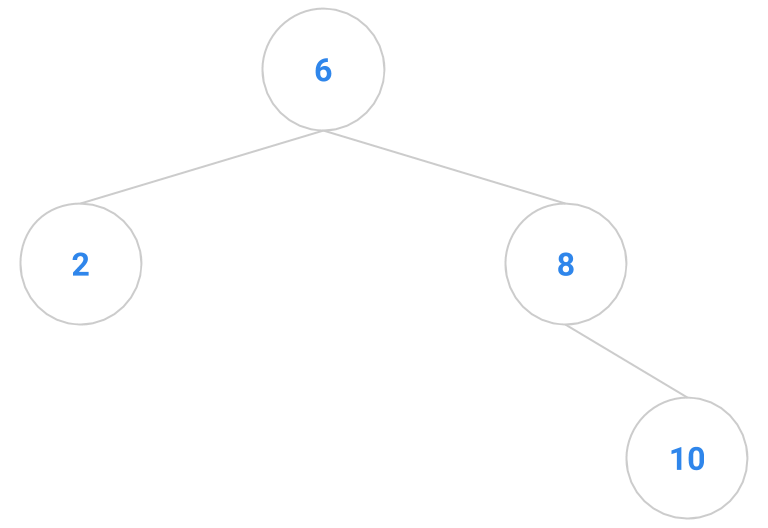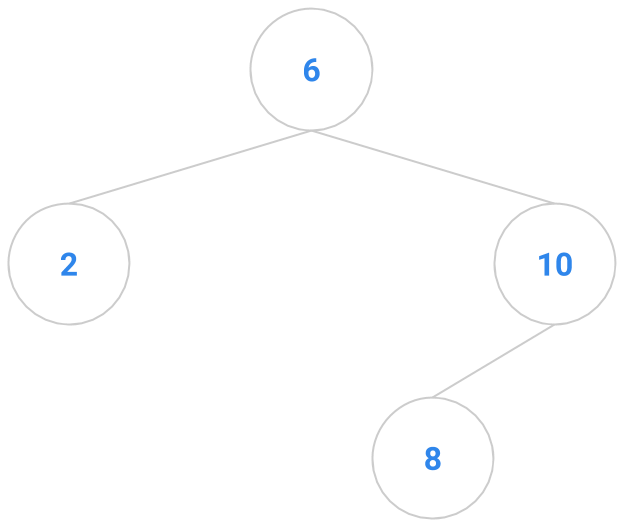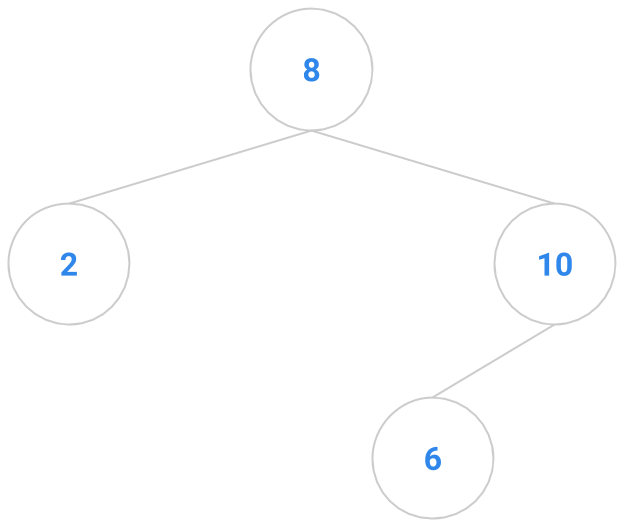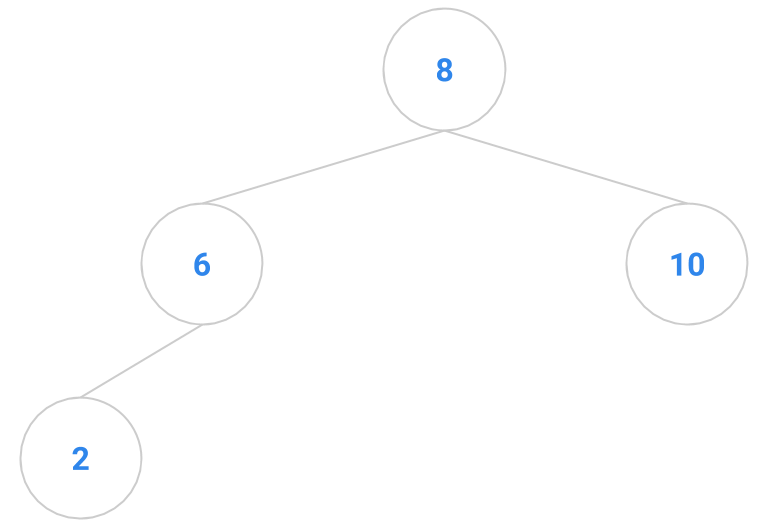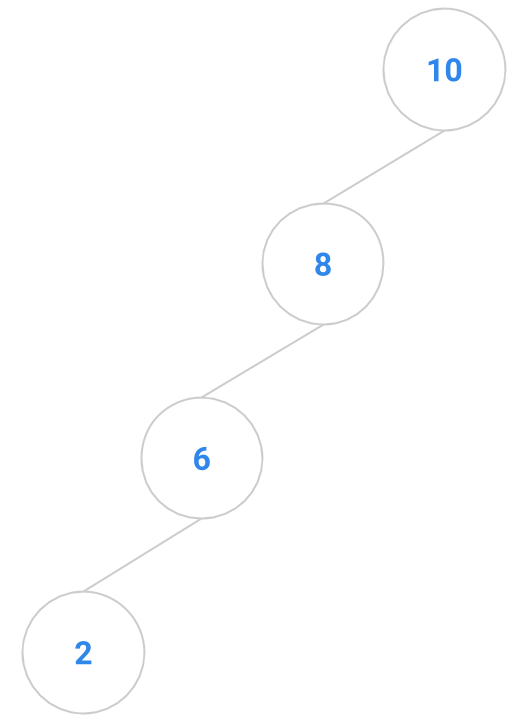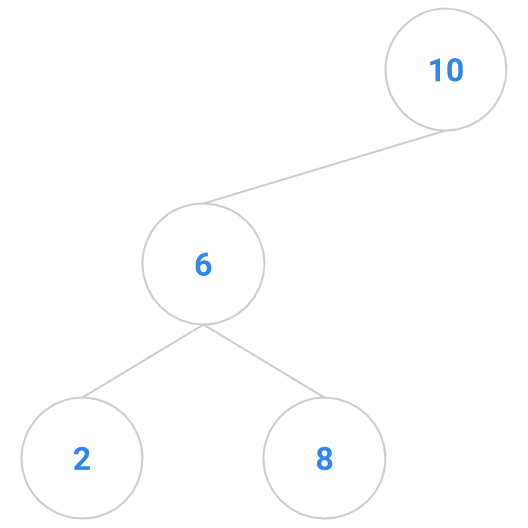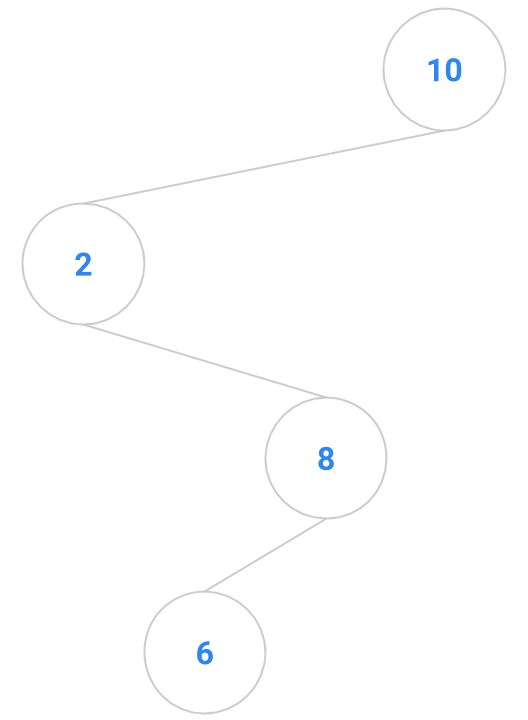A Good Way to Delete a Key

The following algorithm for deletion has the advantage of minimizing restructuring and unbalancing of the tree. The method returns the tree that results from the removal.

1. Find the node to be removed. We’ll call it remNode. If it’s a leaf, remove it immediately by returning null. If it has only one child, remove it by returning the other child node.
2. Otherwise, remove the inorder successor of remNode, copy its item into remNode, and return remNode.

What is an inorder successor? It is the node that would appear AFTER the remNode if you were to do an inorder traversal of the tree.

An example is diagrammed below. The node to remove is the node containing 4. It has two children, so it’s not an easy node to remove. We locate the node with 4’s inorder successor, namely 5. The node containing 5 has no children, so it’s easy to delete. We copy the 5 into the node that formerly contained 4, and delete the node that originally contained 5.

Before	After

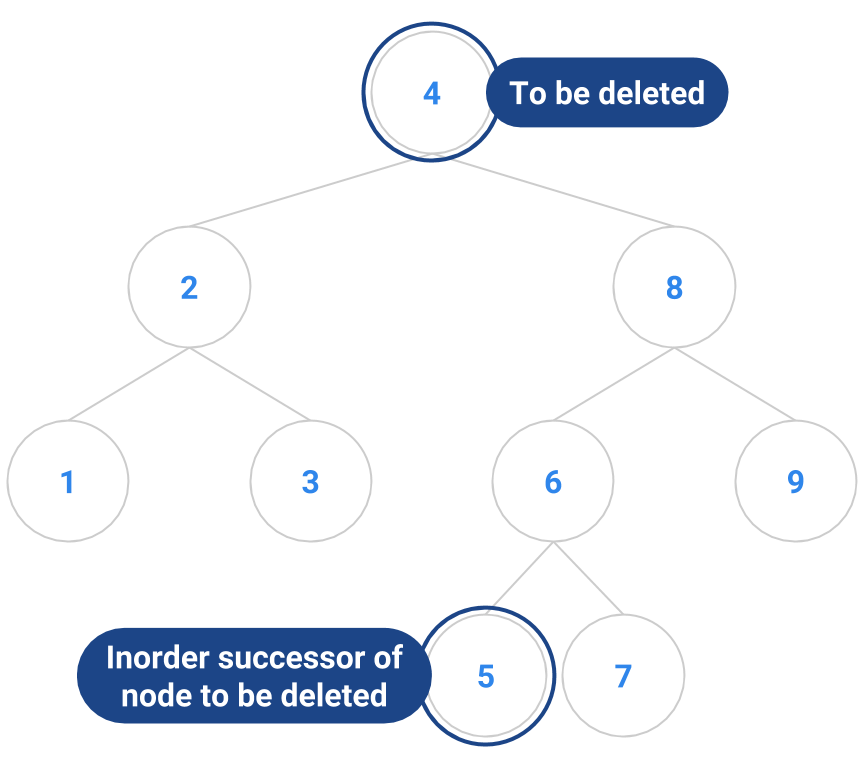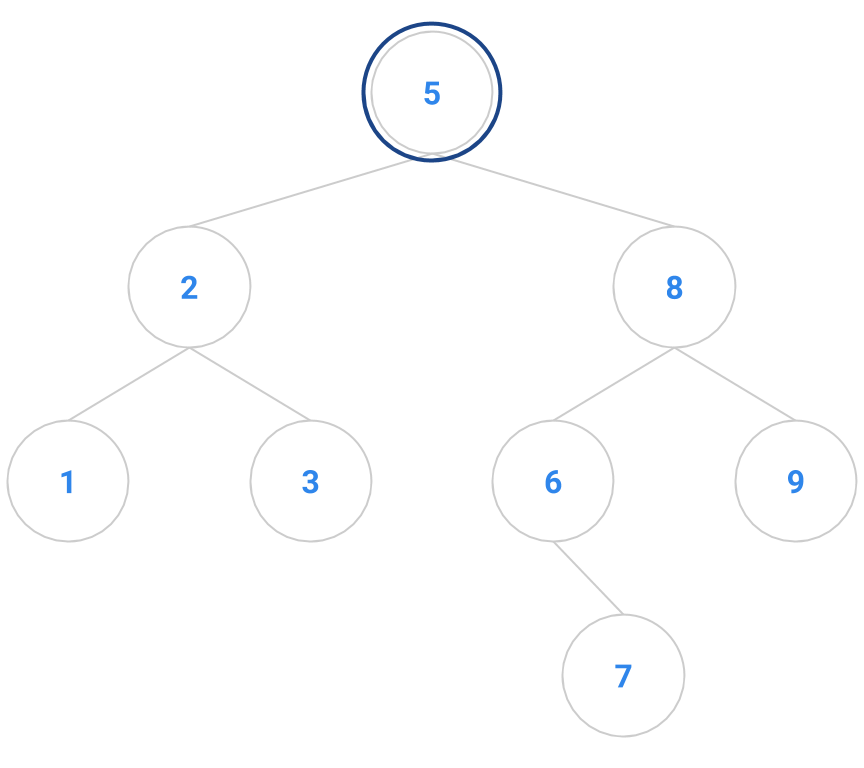Inorder Successor

Suppose node is the root node in a BST with both a left child and a right child. Will sucNode, the inorder successor of node, ALWAYS have a null left child? Discuss this with your partner.

We’ve implemented a delete method for you already. Take a look at it and understand how it works.

The Engineer’s Tradeoff

Consider the problem of finding the kth largest key in a binary search tree. An obvious way of doing this is to use the inorder enumeration from this week’s lab; we could call nextElement until we get the desired key. If k is near the number of keys N in the tree, however, that algorithm’s running time is proportional to N. We’d like to do better. But how?

If you haven’t yet noticed, this class is all about tradeoffs—finding the delicate balance between two conflicting factors to perfectly suit a certain task. Choosing an appropriate data structure is one tradeoff: an algorithm that requires quick access to a certain piece of information would perform better on an array, but an algorithm that uses many insert and delete operations would probably do better in a linked list. Sacrificing a shorter running time in exchange for more memory space, or vice versa, is another.

For this problem, we can reduce the runtime of the kth largest key by storing in each node the size of the tree rooted at that node. Can you design an algorithm using this idea that runs in time proportional to d, where d is the depth of the tree?

Deliverables

Here’s a quick recap of what you need to do to complete this lab!

• Understand how compareTo relates to higher order functions.
• Make the User class implement Comparable.
• Implement getOrderedBy in DBTable.java.
• Complete coding exercises in User.java and DBTable.java.
• Complete the following methods in BinarySearchTree.java:
  • BinarySearchTree()
  • BinarySearchTree(TreeNode root)
  • contains(T key)
  • add(T key)
• Complete and submit the worksheet
• Complete the weekly survey and submit to Gradescope.
• Understand the delete method of the BinarySearchTree.