FAQ #
Each assignment will have an FAQ linked at the top. You can also access it by adding “/faq” to the end of the URL. The FAQ for Lab 5 is located here.
Before You Begin #
Making Your Shared Partner Repository #
Please do not skip this section. Partnerships are strongly recommended for labs. You must complete all partner work for the rest of the semester in the shared repository. See the Collaboration Guide for more information.
If you are looking for a partner, please let your TA know; they’d love to help!
Ensure that your partnership is working from a shared repository. Your shared repo can be created on beacon’s partnerships page.
After adding and committing your own work, you can receive your partner’s work:
$ git pull origin main
Reference the Git WTF guide and lecture one for any git confusions!
Learning Goals for Today #
This lab introduces you to the linked list, a data structure you may remember from CS 61A. Much like an array, a linked list stores sequential data. However linked lists use nodes; each node stores one item and a reference to the next node. The last node in a linked list has no next node, so it stores a null reference instead.
It is possible to implement linked lists that store any type of data by using generics, which you will be learning about in detail in a later lab. For now, this lab will focus on a Linked List that stores only integers - an IntList, for which we have provided a template. In this lab you will implement some basic functional methods for this data structure; in the next lab you will implement some more finicky destructive and non-destructive methods (you’ll get an introduction to these terms later today).
Along the way, we’ll also talk about testing and debugging software engineering principles.
Introduction to Linked Lists #
In the next two labs we’re going to be working with the linked list. A linked list is similar to an array in that it also stores sequential data, but different operations have different runtimes between linked lists and arrays. Since different problems call for different efficient operations, choosing the right data structure is an important design choice for an engineer, and we’ll study this as we go through the course.
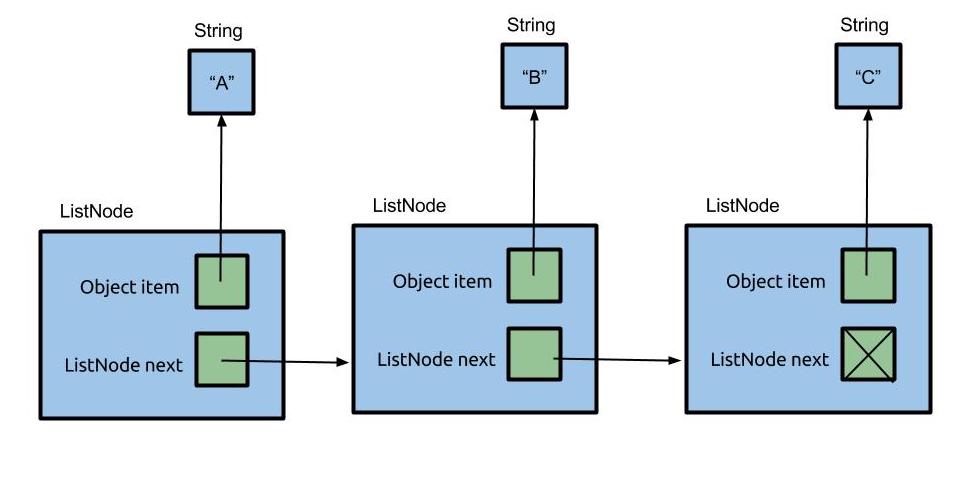
Here’s a picture of a simple implementation of a linked list that contains the items “A”, “B”, and “C” (can you draw the corresponding picture for an array that stores these items?). A linked list consists of nodes that are chained together. Here we represent nodes with a generic class ListNode. Each node contains some item called item. As you can see, the items form a sequence. In this example, the linked list items are Strings, though our linked list will contain ints instead, just like an int[].
IntList #
A Straightforward Implementation of a Linked List #
Here’s an implementation of an IntList which could easily be generalized to store different types of data. Notice how it stores an item item and a reference to another node next.
public class IntList {
public int item;
public IntList next;
}
IntList Box and Pointer Diagram #
Draw out the box and pointer diagram that would result after the following code has been executed. When you and your partner have compared diagrams, check your accuracy using the Java Visualizer below.
public class IntList {
public int item;
public IntList next;
public static void main(String[] args) {
IntList L = new IntList();
L.item = 5;
L.next = null;
L.next = new IntList();
L.next.item = 10;
IntList p1 = L.next;
L.next.next = new IntList();
L.next.next.item = 15;
IntList p2 = p1.next;
p1.next = null;
}
}
If it’s hard to see what’s going on in the Java Visualizer, enable the following two options from the code editor.
- Prefer non-nesting and vertical layouts
- Force linked lists to display vertically
IntList JUnit #
For this lab, we’ve written JUnit tests for you in IntListTest.java. Open it up and read through it. The first thing you’ll notice are the imports at the top. These imports are what give you easy access to the JUnit methods and functionality that you’ll need to run JUnit tests. If you want to read more about JUnit, refer to Lab 4.
Exercise: The get Method #
Fill in the get method in the IntList class. get takes an int position as an argument, and returns the list element at the given (zero-indexed) position in the list.
For example, lets say you have an Intlist with items 44, 79, and 109. If get(1) is called, you should return 79. If the position is out of range, get should throw IllegalArgumentException with an appropriate error message (just type in throw new IllegalArgumentException("YOUR MESSAGE HERE")). Assume get is always called on the first node in the list.
public class IntList {
public int get(int position) {
....
}
}
Once you have something, test your code by running IntListTest.java. Depending on your IntelliJ setup, a window should pop up giving you multiple options. Choose the IntListTest next to the icon with a red and green arrow contained in a rectangle. If your implementation is correct, you should pass the get method tests.
Exercise: toString and equals #
In Lab 2, we introduced you to the toString and equals methods and you worked with a Point class for your Pursuit Curves that implemented these methods.
Implement the standard Java methods, toString and equals, in the IntList class.
Once you’re done, test your code using the provided JUnit tester in
IntListTest.java.
toString- The
toStringmethod forIntListreturns theStringrepresentation of this list, namely:- The
Stringrepresentation of the first element, followed by a space, - The
Stringrepresentation of the second element, followed by a space, - …
- The
Stringrepresentation of the last element.
The list containing the integers 1, 3, and 5 is represented by the string
1 3 5. - The
Hint: How would you convert an integer to a string in Java? #
Try searching for the answer online! Talk to your partner and your peers! Consider referencing the official Java Documentation!
equals- Given an
Objectas argument, this method returnstrueif this list and the argument list are the same length and store equal items in corresponding positions (determined by using the elements’equalsmethod).
Hint: How would you check if the given object is of type IntList? #
IntList? # Check the Java Documentation for a method if you’re unsure.
Exercise: add #
Fill in the add method, which accepts an int as an argument and appends an IntList with that argument at the end of the list. For a list 1 2 3 4 5, calling add with 8 would result in the same list modified to 1 2 3 4 5 8.
public void add(int value) {
// TODO
}
Exercise: smallest #
Implement the smallest method, which returns the smallest int that is stored in the list. For a list 6 4 3 2 3 2 2 5 999, a call to smallest would return 2.
public int smallest() {
// TODO
}
Hint: How do we ask specific questions about integers in Java? #
Exercise: squaredSum #
Finally, implement the squaredSum method. As the name suggests, this method returns the sum of the squares of all elements in the list. For a list 1 2 3, squaredSum should return 1^2 + 2^2 + 3^2 = 1 + 4 + 9 = 14.
public int squaredSum() {
// TODO
}
This type of function is called a reducer, as it reduces the whole list down to a single value! You might remember this idea from CS61A.
Destructive vs. Non-Destructive #
Suppose you have an IntList representing the list of integers 1 2 3 4. You want to find the list that results from squaring every integer in your list, 1 4 9 16.
There are two ways we could go about solving this problem. The first way is to traverse your existing initial IntList and actually change the items stored in your nodes. Such a method is called destructive because it can change (mutate or destroy) the original list.
IntList myList = IntList.of(1, 2, 3, 4);
IntList squaredList = IntList.dSquareList(myList);
System.out.println(myList);
System.out.println(squaredList);
Running the above, destructive program would print,
1 4 9 16
1 4 9 16
Observe that the
IntList.of()method makes it much easier to create IntLists compared to the brute force approach. This might be useful for writing your own tests…. ;)IntList myList = new IntList(0, null); myList.next = new IntList(1, null); myList.next.next = new IntList(2, null); myList.next.next.next = new IntList(3, null); // One line of using IntList.of() can do the job of four lines!
The second way is called non-destructive, because it allows you to access both the original and returned lists after execution. This method returns a list containing enough new IntList nodes such that the original list is left unchanged.
IntList myList = IntList.of(1, 2, 3, 4);
IntList squaredList = IntList.squareList(myList);
System.out.println(myList);
System.out.println(squaredList);
Running the above, non-destructive program would print,
1 2 3 4
1 4 9 16
In practice, one approach may be preferred over the other depending on the problem you are trying to solve and the specifications of the program. We will talk about such trade-offs throughout the rest of the semester!
dSquareList Implementation #
Here is one possible implementation of dSquareList, along with a call to dSquareList.
public static void dSquareList(IntList L) {
while (L != null) {
L.item = L.item * L.item;
L = L.next;
}
}
IntList origL = IntList.of(1, 2, 3)
dSquareList(origL);
// origL is now (1, 4, 9)
The reason that dSquareList is destructive is because we change the values of the original input IntList L. As we go along, we square each value, and the action of changing the internal data persists.
It is also important to observe that the bits in the origL box do not change. Objects are saved by reference, meaning the value tied to the variable will point to a memory address rather than the integer values in our list. Thus, though this method is destructive, it is changing the value saved in the memory location referred to by origL, not the value within origL itself. For more about this, refer to Lab 2.
Testing dSquareList #
The dSquareList implementation above is provided to you in your skeleton file as well.
Use the Java Visualizer plugin to visualize the IntList and to understand how the dSquareList method works, discussing with your partner as you do so. Pointers and IntLists might seem confusing at first, but it’s important that you understand these concepts!
Note: The choice to return void rather than a pointer to L was an arbitrary decision. Different languages and libraries use different conventions (and people get quite grumpy about which is the “right” one). We have the flexibility to decide when writing destructive methods when mutating objects passed in as arguments. Talk to your partner about why this is and try to think of settings where one would be preferable over the other.
Non-Destructive Squaring #
squareListIterative() and squareListRecursive() are both non-destructive. That is, the underlying IntList passed into the methods does not get modified, and instead a fresh new copy is modified and returned.
public static IntList squareListIterative(IntList L) {
if (L == null) {
return null;
}
IntList res = new IntList(L.item * L.item, null);
IntList ptr = res;
L = L.next;
while (L != null) {
ptr.next = new IntList(L.item * L.item, null);
L = L.next;
ptr = ptr.next;
}
return res;
}
public static IntList squareListRecursive(IntList L) {
if (L == null) {
return null;
}
return new IntList(L.item * L.item, squareListRecursive(L.next));
}
Ideally, you should spend some time trying to really understand them, including possibly using the visualizer. However, if you don’t have time, note that the iterative version is much messier.
The iterative versions of non-destructive IntList methods are often (but not always) quite a bit messier than the recursive versions, since it takes some careful pointer action to create a new IntList, build it up, and return it.
Exercise: Concatenation #
To complete the lab, implement dcatenate and catenate as described below. You may find the squaring methods from above to be useful as you write your code.
public static IntList dcatenate(IntList A, IntList B) {
// TODO
}
public static IntList catenate(IntList A, IntList B) {
// TODO
}
Both methods take in two IntLists and concatenate them together, so catenate(IntList A, IntList B) and dcatenate(IntList A, IntList B) both result in an IntList which contains the elements of A followed by the elements of B. The only difference between these two methods is that dcatenate modifies the original IntList A (it’s destructive) and catenate does not.
As an example, if you call either of the methods with two IntLists containing [0, 1, 2] and [3, 4], both catenate and dcatenate will result in an IntList containing [0, 1, 2, 3, 4].
To complete the lab:
- Fill in one of
dcatenate()orcatenate(), and run them against our tests. Revise your code until it passes our tests. - Repeat for the method you haven’t yet completed. (We recommend you do one first and finish it before you start the next, because then you’ll be able to take advantage of the similar logic).
IntList problems can be tricky to think about, and there are always several approaches which can work. Don’t be afraid to pull out pen and paper or go to the whiteboard and work out some examples! If you get stuck, drawing out the pointers can probably steer you back onto the path of progress. And, as always, the debugger is a great option!
Feel free to use either recursion or iteration. For extra practice, try both!
It’s also often useful to first think about base cases, such as when A is null, for example. This works especially well for building up a recursive solution. In other words, write up a solution that would work for the base case, then stop and think about how to expand this solution into something that works for other bigger cases.
For this problem, it is okay for dcatenate to return one or the other list if one or both of A and B are null. For catenate, it is okay to attach B to the end of A without making a full copy of B. However, think about and discuss the following two questions with your partner:
- Why does this still produce a ‘correct’ program?
- What kinds of problems could this decision cause?
Recap #
Today we talked about the IntList. Methods involving Linked Lists can be implemented iteratively and recursively. These functions can also be destructive or non-destructive.
Deliverables #
IntList.javagettoStringequalsaddsmallestsquaredSumcatenatedcatenate
