FAQ #

Each assignment will have an FAQ linked at the top. You can also access it by adding “/faq” to the end of the URL. The FAQ for Lab 16 is located here.

Introduction #

As usual, pull the files from the skeleton and make a new IntelliJ project.

This lab will deal with a new tree data structure - tries. Tries store information in a different way than a traditional tree and as such they can be leveraged to solve certain problems even faster than their more general counterparts.

Tries #

For this lab, you’ll create TrieSet, a Trie-based implementation of the TrieSet61BL interface, which represents a basic Trie.

Up to this point in the course, we have learned about a number of Abstract Data Types, such as Lists, Sets, Maps, and others. Today, we will be exploring another way to implement the Set and Map ADTs, specific to storing Strings.

Suppose you were tasked with creating a Set which is only going to be used to store Strings. In the beginning of the class, we might have tried to just put each String into a link of a LinkedList. If this were the representation we used, how would we implement add(), remove(), and contains()? Even if we took the time to order our LinkedList, we would still have a linear runtime for each of these operations.

Now we should be wondering how we can speed up these runtimes. Recently, we have learned about structures which might help us in our quest for efficiency. Perhaps we could store our Strings in a BST, where each node contains a single String and uses the String compareTo() method when determining which direction to go. This will offer an improvement, since a well-balanced BST will make add() and contains() considerably faster, but repeatedly using add() and remove() might end up causing the BST to lose its balance.

Let us now consider another way to implement this Set of Strings, the trie. This structure, whose name is short for Retrieval Tree, is designed to give a runtime that is \(\Theta(k)\) in the worst case where \(k\) is the number of characters in the String, not the number of Strings contained in our set. This may seem difficult to believe at first, but as we explore the structure of this data structure, we will see that we are simply shifting the runtime dependency to a different aspect of our data, in order to prevent the number of items contained from affecting our runtime.

To create a trie, we must first recognize a few things about the data type we are working with. Firstly, we know that Strings are comprised of individual characters, which can be extracted. Secondly, we know that there are only so many characters available to choose from (after all, our alphabet thankfully does not have infinitely many letters). Given these two facts, we can begin our construction of this data structure.

Suppose we begin with a tree structure where we store a single character at each node. Think about how a single String might be represented; for every letter in given String, we have a node whose child is a node which represents the next letter. This is depicted below, where the word “sam” has been inserted:

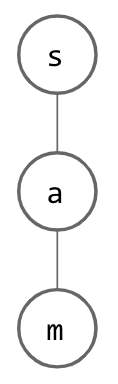
Now, how do we insert another word? If this new word is similar to our initial word, this should be easy, since we can just share nodes that we have in common! Once we reach a letter that is not shared between the two words, we can just add another child to the last node that was shared and continue creating nodes for our new word. Below, we insert “sad” into our tree:

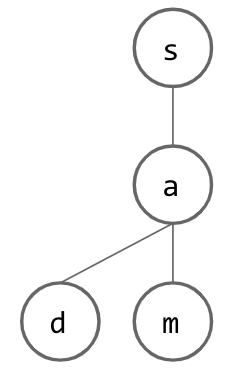
However, if we want to insert a String that does not start with the same letter as our current root, it seems that we are out of luck and need to create an entire additional tree. However, if we instead add a dummy node as our root, we can pretend that each String inserted “begins” with this empty node and go from there. This is what our trie looks like if we use our dummy root idea and insert the String “a”:

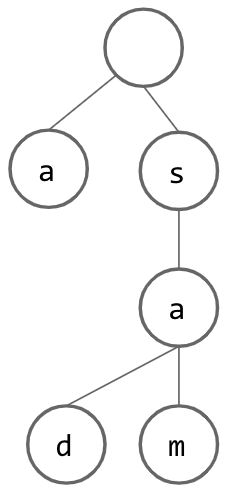
From here, we can continue inserting additional Strings, building up our Set. Below, we have inserted the Strings “same” and “sap”:

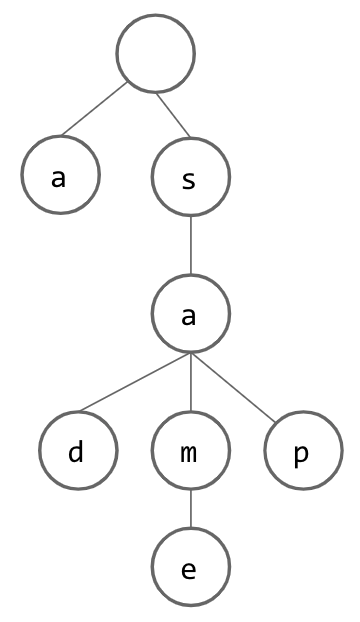
But wait! How do we know which words are actually contained in our set? After all, if we only think of words as being in the trie if they end with a node with no children, then we have lost our String “sam”. If we solve this issue by considering each node in the trie to designate a String, we suddenly have unexpected Strings in our Set (“s” and “sa”). To fix this issue, we add another piece of information to each node: a flag which lets us know whether we have reached the end of a word. Now, our trie will look something like this:

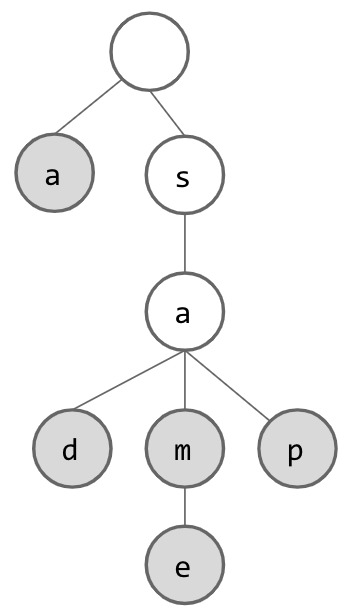
At this point, if we want to search for Strings which are contained within the trie, we can simply look for the appropriate node for each letter as we trace through the trie. If we ever cannot find the next node, we know that the word is not contained. We also know that if we have gone through all of our letters and arrived at a node that exists, we should still check this “flag” to be sure that the word was actually stored in the trie.

Now that we have covered the basic idea of a trie used as a Set, think about how we could turn this Set (of Strings) into a Map (which maps a String to another Object) with a simple change.

One question we have not yet answered is how to properly store the children for each of our nodes. If we know the size of our alphabet, it seems reasonable that we can just store an array that is as long as our alphabet in each node, allowing us to enumerate each letter in our alphabet and store a link to the appropriate child. However, you might see why this would be inefficient; most of our array will likely be empty, as most Strings obey some set of “spelling rules” and certain combinations of letters are much more likely than others (think about how many words start with “an” vs how many words start with “qx”). To account for this, we might want to be more clever with our child-tracking in our nodes. Consider using a BST or an implementation of the Map interface (such as HashMap) as potential ways of keeping track of a node’s children, while considering the pros and cons for each (compare to each other, as well as to our initial array idea).

Optional Tries: Worksheet #

If you would like some additional practice on tries, you can complete questions 2.1 on Spring 2019’s Discussion 9.

Once you have made finished you can check your work with the solutions.

Exercise: MyTrieSet #

Create a class MyTrieSet that implements the TrieSet61BL interface using a trie as its core data structure (You are not allowed to import any built in trie implementations). You must do this in a file named MyTrieSet.java. Your implementation is required to implement all of the methods given in TrieSet61BL except for longestPrefixOf. For longestPrefixOf you should throw an UnsupportedOperationException.

You can test your implementation using the TestMyTrieSet class. You’ll notice that our given tests make a few assumptions on correctness of add. Make sure you write your own test for add and properly test the method before proceeding to test the other methods!

Deliverables #

• Complete the MyTrieSet.

Submission Notes #

• The autograder has one tests with 0 points for Tries. This is because we did not require you to implement longestPrefixOf.