FAQ #

Each assignment will have an FAQ linked at the top. You can also access it by adding “/faq” to the end of the URL. The FAQ for Lab 10 is located here.

Introduction #

As usual, pull the files from the skeleton and open the Lab 10 directory in IntelliJ.

In this lab, we will introduce another data structure called a tree (you might have already seen this in CS 61A or another equivalent course). The meaning of the tree data structure originates from the notion of a tree in real life.

Below is a conceptual visualization of a tree. It’s not really a box and pointer diagram and should not be interpreted as a literal implementation in Java.

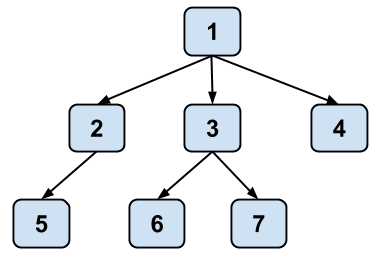
Note that while a tree in real life is rooted at the bottom and branches out and upwards, trees in computer science are typically drawn such that they are rooted at the top and branch out and downwards.

For this lab, we have not provided you with any local tests. Instead, we expect you to create your own test file and write your own tests! You can also use ad-hoc testing in the main methods to test quickly.

Vocabulary #

In order to be able to talk about trees, we first need to define some terminology.

Term	Description	Example Above
Node	Single element in a tree	1, 2, 3, 4, 5, 6, and 7 are all nodes.
Edge	A connection between two nodes	There is a direct edge from 1 to 2, but there is no direct edge from 1 to 7.
Path	A series of one or more edges that connects two nodes without using an edge more than once	There is a path from 1 to 7, consisting of edges 1 -> 3 and 3 -> 7.
Leaf	A node with no children	4, 5, 6, and 7 are leaf nodes.
Root	The topmost node, which does not have a parent	1 is the root node.

Relationships #

These following terms are defined with respect to a particular node.

Term	Description
Child	A node directly below the current node
Parent	Single node connected directly above the current node
Siblings	Nodes with the same parent
Ancestors	All nodes on the path from the selected node up to and including the root
Descendants	All the children, children’s children, and so forth of a node
Subtree	The tree consisting of the node and all of its descendants
Height	The length of the path from the node to its deepest descendant. By length, we mean the number of nodes traveled along a given path. Therefore, the height of a leaf node is 1. (Note: There is an alternate definition of height as the number of edges traversed. In that case, the height of a leaf would be 0.)
Depth	The length of the path from the node to the root. The depth of the root node is 0.

Sometimes we’ll refer to the height and depth of a tree as a whole. In these cases, it’s usually assumed that we’re referring to the height of the root node and the depth of the deepest leaf, respectively.

Definition #

For a linked structure of nodes to be considered a tree:

• nodes must have either no parents or 1 parent
• there can be no cycles (paths that start and end at the same node)
• there can only be one path between any two nodes in a tree
• all nodes must be a descendant of the root (except the root itself)

Discussion: Examples of Trees #

Discuss with your partner whether the following examples would be considered trees as we’ve introduced them above.

• Linked List
• Family Tree

Trees are naturally recursive structures, so you’ll find that we implement a lot the methods in this lab using recursion because it tends to be the simplest solution. Unlike linked lists, trees can have one or more children which can make iterative approaches more difficult (this ultimately depends on the structure / implementation of your tree).

Amoeba Family Tree #

An amoeba family tree is an example of our above definition of a tree that you will be working with for this lab. It is simpler than a normal family tree because amoebas do not need partners in order to reproduce. An amoeba has one parent, zero or more siblings, and zero or more children. An amoeba also has a name.

Below is the skeleton code for an Amoeba. The full code is located in the AmoebaFamily.java file.

class Amoeba {
    public String name;
    public Amoeba parent;
    public ArrayList<Amoeba> children;
}

And below is a box and pointer diagram of our Amoeba.

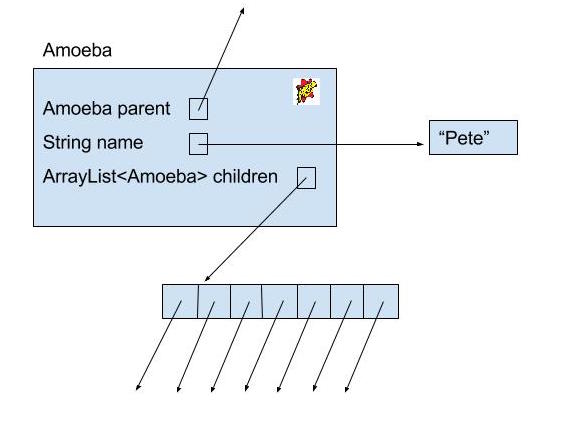
Amoebas (or amoebae) live dull lives. All they do is reproduce, so all we need to keep track of them are the following methods:

/* Creates an AmoebaFamily, where the first Amoeba's name is NAME. */
public AmoebaFamily(String name) {
    root = new Amoeba(name, null);
}

/* Adds a new Amoeba with childName to this AmoebaFamily as the youngest
   child of the Amoeba named parentName. This AmoebaFamily must contain an
   Amoeba named parentName. */
public void addChild(String parentName, String childName) {
    if (root != null) {
        root.addChildHelper(parentName, childName);
    }
}

The Amoeba objects are the nodes of our tree, represented by the AmoebaFamily object. You will find that most of the methods of this AmoebaFamily will be implemented through recursive helper methods of the Amoeba class.

This organization structure should feel similar. Before for our DLList we had the DLList class and within it the inner class Node. The DLList encapsulated the recursive structure of the Nodes. Now we will have our AmoebaFamily which will encapsulate the recursive structure of the Amoebas.

Void Recursive Methods #

In the AmoebaFamily class, we provide the method addChild to add a new Amoeba to the AmoebaFamily tree. The method implements a general traversal of the tree using a void recursive method in the Amoeba class. Read through this method and related functionality to get an understanding of how we are traversing and manipulating the Object.

Non-void Recursive Methods #

So far, the methods we’ve seen for the AmoebaFamily class have not returned anything; they have only been modifying the state of the AmoebaFamily. We will be able to do cooler things if we can return values, and the next example will take advantage of this.

Exercise: longestName #

Implement the longestName method in the AmoebaFamily class. Make this as similar to longestNameLength as possible. You will find that these non-void recursive methods follow a specific pattern, one that you will likely draw upon again when solving problems that you face in the future.

You will not need to use longestNameLength directly in your implementation of longestName.

Binary Trees #

We’ll now move on from trees and explore a common, special case of the tree data structure: the binary tree. A binary tree is a tree in which each node has at most two children. Rather than store the children in an ArrayList as was done in Amoeba nodes, one normally just has two separate variables left and right for the left and right children of the binary tree.

Exercise: BinaryTree #

The file BinaryTree.java defines a BinaryTree class and a TreeNode class. First, read over the code and then implement the following three methods.

Note: you may use the sampleTreeX methods to generate sample trees to test the functions that you write. In addition, consider writing your own methods to generate more trees to test your code.

Exercise 1: height #

First, if you have a partner, switch which partner is coding if you haven’t recently.

Implement the height method in the BinaryTree class. The height of an empty tree is 0; the height of a one-node tree is 1; the height of any other tree is 1 + the greater of the heights of the two children.

Exercise 2: isCompletelyBalanced #

Add an isCompletelyBalanced method for the BinaryTree class. A tree with no nodes and a tree with one node are both completely balanced; any other tree is completely balanced if and only if the height of its left child is equal to the height of its right child, and its left and right children are also completely balanced. Make sure you test your code with trees of height 3 or more to ensure that your code works!

Exercise 3: fibTree #

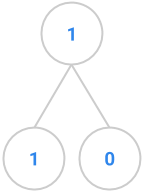
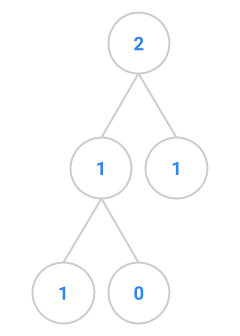
This exercise deals with “Fibonacci trees”, trees that represents the recursive call structure of the Fibonacci computation. (The Fibonacci sequence is defined as follows: \(F_0 = 0, F_1 = 1\), and each subsequent number in the sequence is the sum of the previous two.) The root of a Fibonacci tree should contain the value of the Nth Fibonacci number, the left subtree should be the tree representing the computation of the N-1th Fibonacci number, and the right subtree should be the tree representing the computation of the N-2th Fibonacci number. The two exceptions to this rule are when we pass in 0 or 1 to the fibTree method. The first few Fibonacci trees appear below.

Function	Tree
fibtree(0)
fibtree(1)
fibtree(2)
fibtree(3)
fibtree(4)
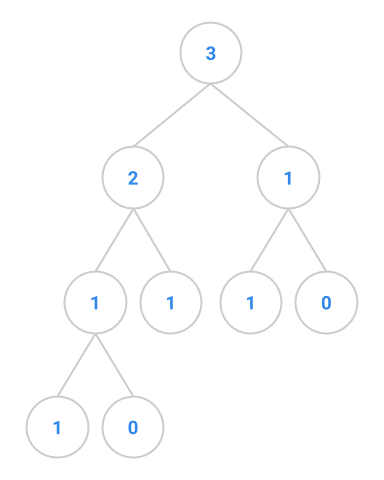fibtree(5)

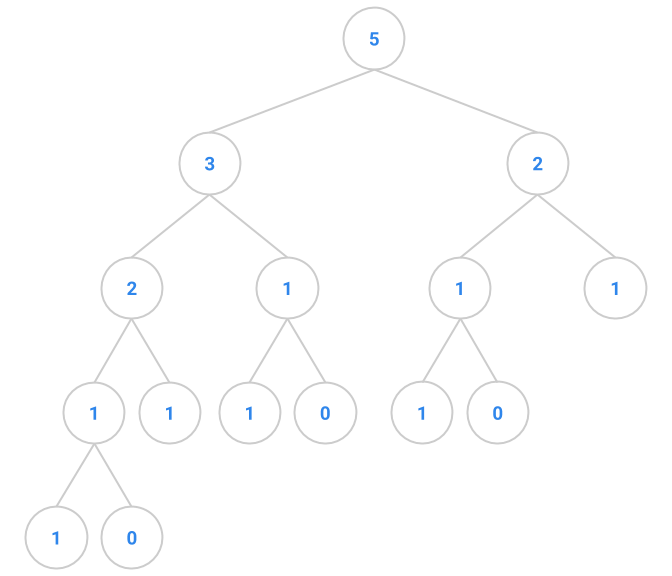Write the static fibTree method in BinaryTree that takes in a non-negative integer N, and returns a BinaryTree that stores the N-th Fibonacci value using the representation above.

Remember how we’ve been delegating structuring all our methods so far for the best code!

Traversals #

The remainder of this lab will cover the tools and techniques related to traversing the notes of a tree structure.

Three processing sequences for nodes in a binary tree occur commonly enough to have names:

• preorder: process the root, process the left subtree (in preorder), process the right subtree (in preorder)

• postorder: process the left subtree (in postorder), process the right subtree (in postorder), process the root.

• inorder: process the left subtree (in inorder), process the root, process the right subtree (in inorder).

Note that for preorder and postorder, it can often be equally valid to process the right and then the left, although it depends on the application. In this course we will typically assume that the processing will be done left and then right unless we specify otherwise. On most exams we will be precise in what order nodes will be processed.

Exercise: Processing Sequences #

With your partner, determine the preorder, inorder, and postorder processing sequence for the tree below. This exercise will not be graded, but understanding how traversals work is a crucial part of understanding how to operate on trees. We will rely on these for many topics in the rest of the course.

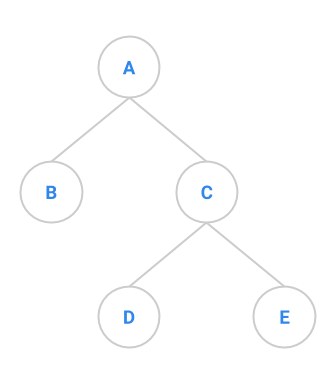
Answers below (highlight to reveal):

Pre Order: A B C D E

Post Order: B D E C A

In Order: B A D C E

Stacks and Queues #

Before we go into more traversals, we will go over some a few more data structures that will help us when we implement the traversals later in the lab.

One of the first true data structures we encountered was the LinkedList data structure. That data structure allowed for adding and removing at any position. However sometimes that is too powerful and we do not need all of that functionality. Thus, we will introduce the stack and the queue data structures, which are like lists, but have more limited, precise functionality. As you go through this section, think about how you can implement stacks and queues by using a LinkedList.

A stack models a stack of papers, or plates in a restaurant, or boxes in a garage or closet. A new item is placed on the top of the stack, and only the top item on the stack can be accessed at any particular time. Stack operations include the following:

• Pushing an item onto the stack.
• Accessing the top item of the stack.
• Popping the top item off the stack.
• Checking if the stack is empty.

As a result, we often refer to stacks as processing in LIFO (last-in, first-out) ordering.

A queue is a waiting line. As with stacks, access to a queue’s elements is restricted. Queue operations include:

• Adding an item to the back of the queue.
• Accessing the item at the front of the queue.
• Removing the front item.
• Checking if the queue is empty.

As a result, we often refer to queues as processing in FIFO (first-in, first-out) ordering.

Exercise: Stacks and Queues #

Exercise 1 #

Suppose that the following sequence of operations is executed using an initially empty stack. What ends up in the stack?

push A
push B
pop
push C
push D
pop
push E
pop

Answer below (highlight to reveal) Note the ordering is such that the bottom of the stack is to the left and the top of the stack is to the right:

Answer: A C

Exercise 2 #

Suppose that the following sequence of operations is executed using an initially empty queue. What ends up in the queue?

add A
add B
remove
add C
add D
remove
add E
remove

Answer below (highlight to reveal) Note the ordering is such that the front of the queue is to the left and the back of the queue is to the right:

Answer: D E

Stacks and Queues: Building a Tree Iterator #

We now consider the problem of returning the elements of a tree one by one, using an iterator. To do this, we will implement the interface java.util.Iterator. The first technique to traverse trees that we will examine is depth-first iteration or depth-first search. The general idea is that we walk along each branch, traveling as far down each branch as possible before turning back and examining the next one. This depth first search traversal should feel similar to the preorder and postorder we defined above. See if you can see the connection!

We will also use a nested iterator class to hide the details of the iteration from the outer class. As with previous iterators, we need to maintain state-saving information that lets us find the next tree element to return, and we now must determine what that information might include. To help work this out, we’ll consider the sample tree below, with elements to be returned depth first as indicated by the numbers.

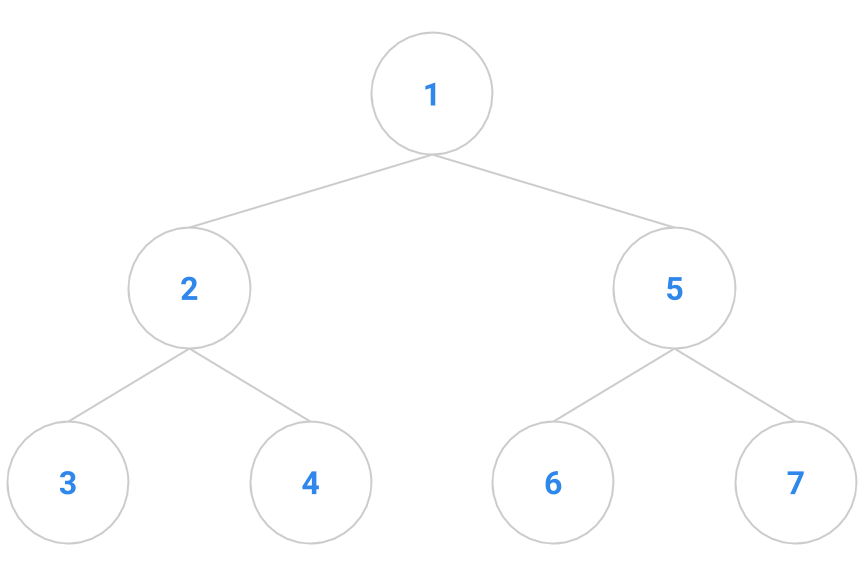
The first element to be returned is the one labeled “1”. Once that’s done, we have a choice whether to return “2” or “5”.

Suppose we break ties by lowest node label. As a result, based on our tie-breaking rule, we will pick “2” over “5”. Once we return element “2”, we have a choice between return “3” or “4” next. But don’t forget about “5” from earlier!

Next, we return “3”, again based on our tie-breaking rule. At this point, we still remember that we need to return to “4” and “5” as in the diagram below.

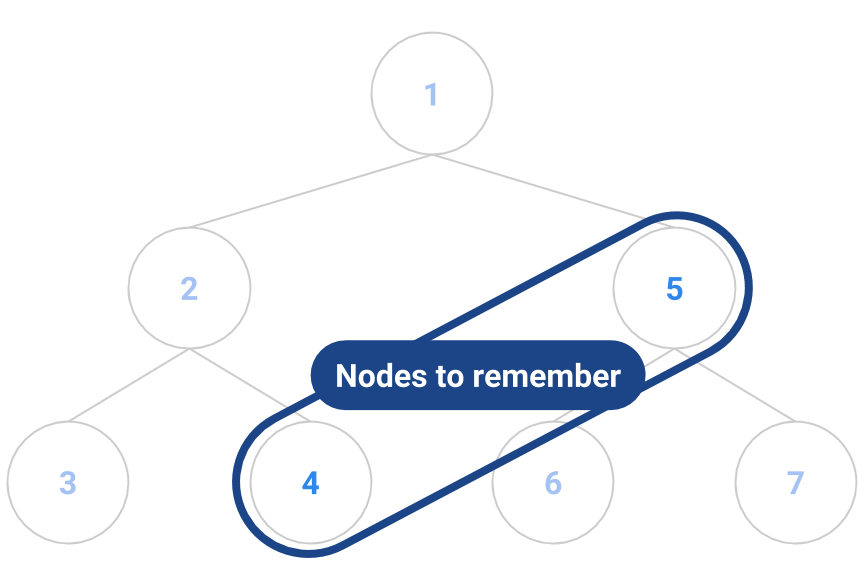
That means that our state-saving information must include not just a single pointer of what to return next, but a whole collection of “bookmarks” to nodes we’ve passed along the way.

More generally, we will maintain a collection that we’ll call the fringe, containing all the nodes in the tree that are candidates for returning next. The next method will choose one of the elements of the fringe as the one to return, then add the returned element’s children to the fringe as candidates for the next element to return. hasNext returns true when the fringe isn’t empty.

The iteration sequence will then depend on the order we take nodes out of the fringe. Depth-first iteration, for example, results from storing the fringe elements in a stack, a last-in first-out structure. The java.util class library conveniently contains a Stack class with push and pop methods. We illustrate this process on a binary tree in which TreeNodes have 0, 1, or 2 children named left and right. Here is the code:

public class DepthFirstIterator implements Iterator<TreeNode> {

    /* Where we will store our bookmarks. */
    private Stack<TreeNode> fringe = new Stack<TreeNode>();

    public DepthFirstIterator(TreeNode root) {
        if (root != null) {
            fringe.push(root);
        }
    }

    /* Returns whether or not we have any more "bookmarks" to visit. */
    public boolean hasNext() {
        return !fringe.isEmpty();
    }

    /* Throws an exception if we have no more nodes to visit in our traversal.
       Otherwise, it picks the most recent entry to our stack and "explores" it.
       Exploring it requires visiting the node and adding its children to the
       fringe, since we must eventually visit them too. */
    public TreeNode next() {
        if (!hasNext()) {
            throw new NoSuchElementException("tree ran out of elements");
        }
        TreeNode node = fringe.pop();
        if (node.right != null) {
            fringe.push(node.right);
        }
        if (node.left != null) {
            fringe.push(node.left);
        }
        return node;
    }

    /* This is left unimplemented for this example. */
    public void remove() {
        throw new UnsupportedOperationException();
    }
}

Exercise: Stack Contents #

For the following exercises, assume that we push the right child before the left child of a node onto the fringe.

Exercise 1 #

What numbers are on the stack when element 4 in the tree below has just been returned by next?

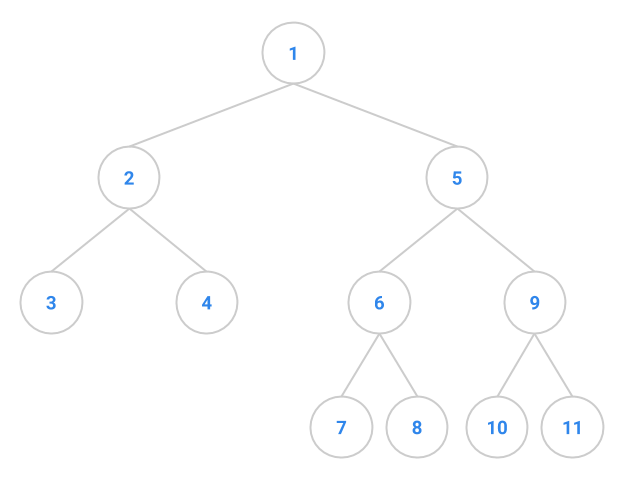
Answer below (highlight to reveal) Note the ordering is such that the front of the queue is to the left and the back of the queue is to the right:

Answer: 5

Exercise 2 #

For the same image above, what numbers are on the stack when element 6 in the tree below has just been returned by next?

Answer below (highlight to reveal) Note the ordering is such that the front of the queue is to the left and the back of the queue is to the right:

Answer: 7 8 9

Exercise 3 #

Suppose the next code pushes the left child onto the stack before the right:

if (node.left != null) {
    fringe.push(node.left);
}
if (node.right != null) {
    fringe.push(node.right);
}

In what order are the elements of the tree above returned?

Answer below (highlight to reveal):

Answer: 1 5 9 11 10 6 8 7 2 4 3

Optional Exercise: Tree Iterators #

Optional Exercise 1: AmoebaDFSIterator #

Switch which partner is doing the coding if you have not done so recently.

Complete the definition of the AmoebaDFSIterator class (within the AmoebaFamily class). It should successively return names of Amoebas from the family in depth-first preorder. You will need to add Amoebas to the stack as you do above, with the right child being pushed before the left child. Thus, for the family set up in the AmoebaFamily main method, the name “Amos McCoy” should be returned by the first call to next; the second call to next should return the name “mom/dad”; and so on. Do not change any of the framework code.

Organizing your code as described in the previous step will result in a process that takes time proportional to the number of Amoebas in the tree to return them all. Moreover, the constructor and hasNext both run in constant time, while next runs in time proportional to the number of children of the element being returned.

Add some code at the end of the AmoebaFamily main method to test your solution. We suggest using the tree examples and answers above as a starting point for your tests.

Optional Exercise 2: AmoebaBFSIterator #

Now write the AmoebaBFSIterator class (within the AmoebaFamily class). This will result in Amoeba names being returned in breadth-first order. That is, the name of the root of the family will be returned first, then the names of its children (oldest first), then the names of all their children, and so on. Another way to think about breadth-first search is a level order traversal. All of the nodes at depth 0 will be processed, then at depth 1, then at depth 2, etc.

Your code for your AmoebaBFSIterator should be very similar to that of AmoebaDFSIterator with one big exception. In AmoebaBFSIterator instead of using a stack you should use a queue. By making this one change you will greatly alter the behavior of your iterator. We recommend using java.util.LinkedList to implement your queue.

There is a java.util.Queue but it is just an interface. There are a number of Java classes which implement this interface, one of which being java.util.LinkedList. Any non-abstract subclass of this interface should work for this exercise.

For the family constructed in the AmoebaFamily main method, your modification will result in the following iteration sequence:

Amos McCoy
mom/dad
auntie
me
Fred
Wilma
Mike
Homer
Marge
Bart
Lisa
Bill
Hilary

Note: You will need to change the return value of the iterator method to AmoebaBFSIterator to see the above output.

Before implementing this, try working out this traversal on paper with the prior exercises to gain intuition for it. Keep track of the state of the queue during the traversal and try to see how the difference between the queue’s FIFO behavior and the stack’s LIFO behavior results in a different traversal.

Conclusion #

Extra Readings #

The next lab will cover binary search trees. You may find Shewchuk’s notes on Binary Search Trees helpful.

Deliverables #

To finish this lab, make sure to finish the following:

• Read through the lab and understand how the AmoebaFamily and BinaryTrees work. Make sure to also read through the section on Stacks and Queues.
• Read through and understand the conceptual exercises. Discuss your answers with your partner or neighbor.
• Complete the following methods in AmoebaFamily:
  • public String longestName()
• Complete the following methods in BinaryTree:
  • public int height()
  • public boolean isCompletelyBalanced()
  • public static BinaryTree fibTree()