FAQ #
Each assignment will have an FAQ linked at the top. You can also access it by adding “/faq” to the end of the URL. The FAQ for Lab 22 is located here.
Introduction #
As usual, pull the files from the skeleton and make a new IntelliJ project.
For demos of the algorithms discussed in this lab, look here
This lab is very reading-heavy, with fairly short coding sections. You should try to fully understand each section before moving on. If you have any confusion, clarify with an AI or your TA!
Average-Case Runtimes #
Before we talk about the topics of today’s lab, let’s talk about insertion sort and quicksort’s runtime in the “average” case.
Runtime Summaries (Optional, but HIGHLY Suggested) #
Insertion Sort #
Let’s consider first the case of insertion sort, and define the idea of an inversion. An inversion is a pair of elements \(j\) and \(k\) such that \(j\) is less than \(k\) but \(j\) comes after \(k\) in the input array. That is, \(j\) and \(k\) are out of order.
This means that the maximum number of inversions in an array is bounded by the number of pairs, and is \(\frac{N(N - 1)}{2}\).
For every inversion, insertion sort needs to make one swap. Convince yourself
that this is true with an example: in the array [1, 3, 4, 2], there are two
inversions, (3, 2) and (4, 2), and the key 2 needs to be swapped backward
twice to be in place. Thus the runtime of insertion sort is \(\Theta(N + k)\),
where \(k\) is the number of inversions. Hence, if \(k\) is small, linear, or
even linearithmic, insertion sort runs quickly (just as fast as, or even faster
than, merge sort and quicksort).
How many inversions are in an average array? Every pair of numbers has an equal chance of being either inverted or not inverted, so the number of inversions is uniformly distributed between 0 and \(\frac{N(N - 1)}{2}\); thus the expected (average) number of inversions is precisely the middle, \(\frac{N(N - 1)}{4}\). This value is in \(\Theta(N^2)\), so insertion sort’s average case runtime is \(\Theta(N^2)\).
Quicksort #
The average case runtime of quicksort depends on the pivot chosen. Recall that in the best case, the pivot chosen is the median, meaning 50% of the elements are on either side of the pivot after partitioning.
The worst possible pivot is the smallest or largest element of the array, meaning 0% or 100% of the elements are on either side of the pivot after partitioning.
Assuming the choice of pivot is uniformly random, the split obtained is uniformly random between 50/50 and 0/100. That means in the average case, we expect a split of 25/75. This gives a recursion tree of height \(\log_\frac{4}{3}(N)\) where each level does \(N\) work. Then quicksort still takes \(O(N \log N)\) time in the average case.
How often does the bad-pivot case come up if we pick pivots uniformly at random? If we consider half of the array as bad pivots, as the array gets longer, the probability of picking a bad pivot for every recursive call to quicksort exponentially decreases.
For an array of length 30, the probability of picking all bad pivots is \(\frac{1}{2}^{30} = 9.3 \cdot 10^{-10}\), which is approximately the same as winning the Powerball: \(3.3 \cdot 10^{-9}\).
For an array of length 100, the probability of picking all bad pivots, \(7.8 \cdot 10^{-31}\), is so low that if we ran quicksort every second for 100 billion years, we’d still have a significantly better chance of trying to win the lottery in one ticket.
Of course, there’s the chance you pick something in between, and the analysis can get far more complicated, especially with variants of quicksort. For practical purposes, in this course, we treat quicksort like it’s in \(O(N \log N)\). For a more in-depth treatment, sign up for CS174!
A Sorting Lower Bound #
Is it possible to do better than \(O(N \log N)\) in the worst case for these comparison-based sorts?
Suppose we have a scrambled array of \(N\) numbers, with each number from \(1\) to \(N\) occurring once. How many possible orders can the numbers be in?
The answer is \(N!\), where \(N! = 1 * 2 * 3 * \dots * (N - 2) * (N - 1) * N\). Here’s why: the first number in the array can be anything from \(1\) to \(N\), yielding \(N\) possibilities. Once the first number is chosen, the second number can be any of the remaining \(N - 1\) numbers, so there are \(N(N - 1)\) possible choices of the first two numbers. The third number can be any of the remaining \(N - 2\) numbers, yielding \(N * (N - 1) * (N - 2)\) possibilities for the first three numbers. We can continue this reasoning to get a total of \(N!\) arrangements of the numbers \(1\) to \(N\).
Each different order is called a permutation of the numbers, and there are \(N!\) possible permutations. You will learn much more about permutations in CS70.
Observe that if \(N\) > 0,
\[N! = 1 * 2 * \dots * (N - 1) * N \leq N * N * N * \dots * N * N * N = N^N\]and (supposing \(N\) is even)
\[N! = 1 * 2 * \dots * (N - 1) * N \geq \frac{N}{2} * (\frac{N}{2} + 1) * \dots * (N - 1) * N \geq \frac{N}{2}^{\frac{N}{2}}\]so
\[\frac{N}{2}^{\frac{N}{2}} \leq N! \leq N^N\]Now let’s look at the logarithms of both these values:
\[\log(\frac{N}{2}^{\frac{N}{2}}) = \frac{N}{2} \log (\frac{N}{2})\] \[\log (N^N) = N \log N\]Both of these values are in \(\Theta(N \log N)\). Hence, \(\log(N!)\) is also in \(\Theta(N \log N)\).
A comparison-based sort is one in which all decisions are based on comparing keys (generally done by “if” statements). All actions taken by the sorting algorithm are based on the results of a sequence of true/false questions. All of the sorting algorithms we have studied so far are comparison-based.
Suppose that two computers run the same sorting algorithm at the same time on two different inputs. Suppose that every time one computer executes an “if” statement and finds it true, the other computer executes the same “if” statement and also finds it true; likewise, when one computer executes an “if” and finds it false, so does the other. Then both computers perform exactly the same data movements (e.g. swapping the numbers at indices i and j) in exactly the same order, so they both permute their inputs in exactly the same way.
A correct sorting algorithm must generate a different sequence of true/false answers for each different permutation of \(1\) to \(N\), because it takes a different sequence of data movements to sort each permutation. There are \(N!\) different permutations, thus \(N!\) different sequences of true/false answers.
If a sorting algorithm asks \(d\) true/false questions, it generates less than or equal to \(2^d\) different sequences of true/false answers. If it correctly sorts every permutation of \(1\) to \(N\), then \(N! \leq 2^d\), so \(\log_2(N!) \leq d\), and \(d\) is in \(\Omega(N \log N)\). The algorithm spends \(\Omega(d)\) time asking these \(d\) questions. Hence,
EVERY comparison-based sorting algorithm takes \(\Omega(N \log N)\) worst-case time.
If we haven’t convinced you of this fact, watch this video from Hug on the amazing game “puppy cat dog”.
This is an amazing claim, because it doesn’t just analyze one algorithm. It says that of the thousands of comparison-based sorting algorithms that haven’t even been invented yet, not one of them has any hope of beating \(O(N \log N)\) time for all inputs of length \(N\).
In the worst case, a comparison-based sort (with 2-way decisions) must take at least \(\Omega(N \log N)\) time. But what if instead of making a 2-way true/false decision, we make a k-way decision?
A Linear Time Sort #
Before diving in, we recommend watching this video on LSD sort made by last summer’s instructor and counting sort to introduce the ideas in the following sections.
Suppose we have an array of a million Strings, but we happen to know that
there are only three different varieties of Strings in it: “cat”, “dog”, and
“person”. We want to sort this array to put all the cats first, then all the
dogs, then the people. How would we do it? We could use merge sort or quicksort
and get a runtime proportional to \(N \log N\), where \(N\) is roughly one
million, but can we do better?
We can propose an algorithm called counting sort. For the above example, it works like this:
-
First, let’s create an integer array of size three called the
countsarray. This array will count the total number of eachString, where “cat” will correspond tocounts[0], “dog” will correspond tocounts[1], and “person” will correspond tocounts[2]. -
Then, let’s iterate through the input array and update the
countsarray. Every time you find “cat”, “dog”, or “person”, incrementcounts[0],counts[1], andcounts[2]by 1 respectively. As an example, the result could be this: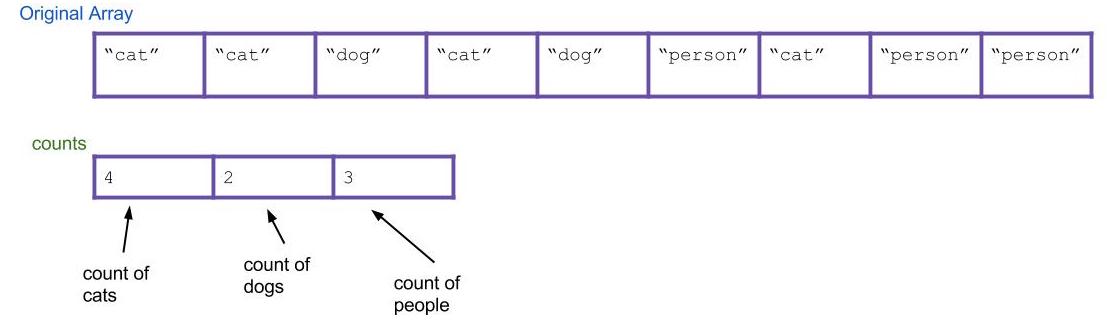
-
Next, let’s create a new
Stringarray calledsortedthat will eventually be your sorted array.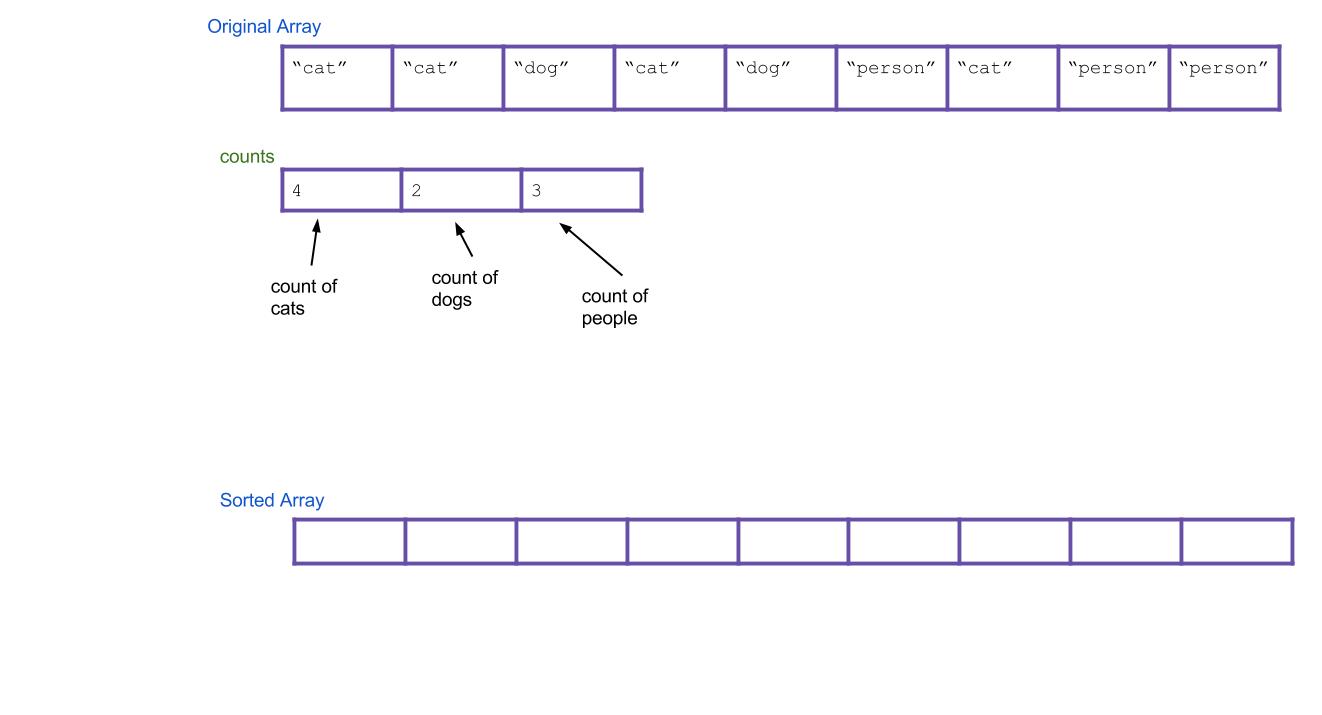
-
Now, based on our
countsarray, can we tell where the first “dog” would go in the new array? How about the first “person”? To do this, we should create a new array calledstartsthat holds this information. We can get this by scanning through the counts array and finding the total number of items to the left of indexi. For our example, the result is: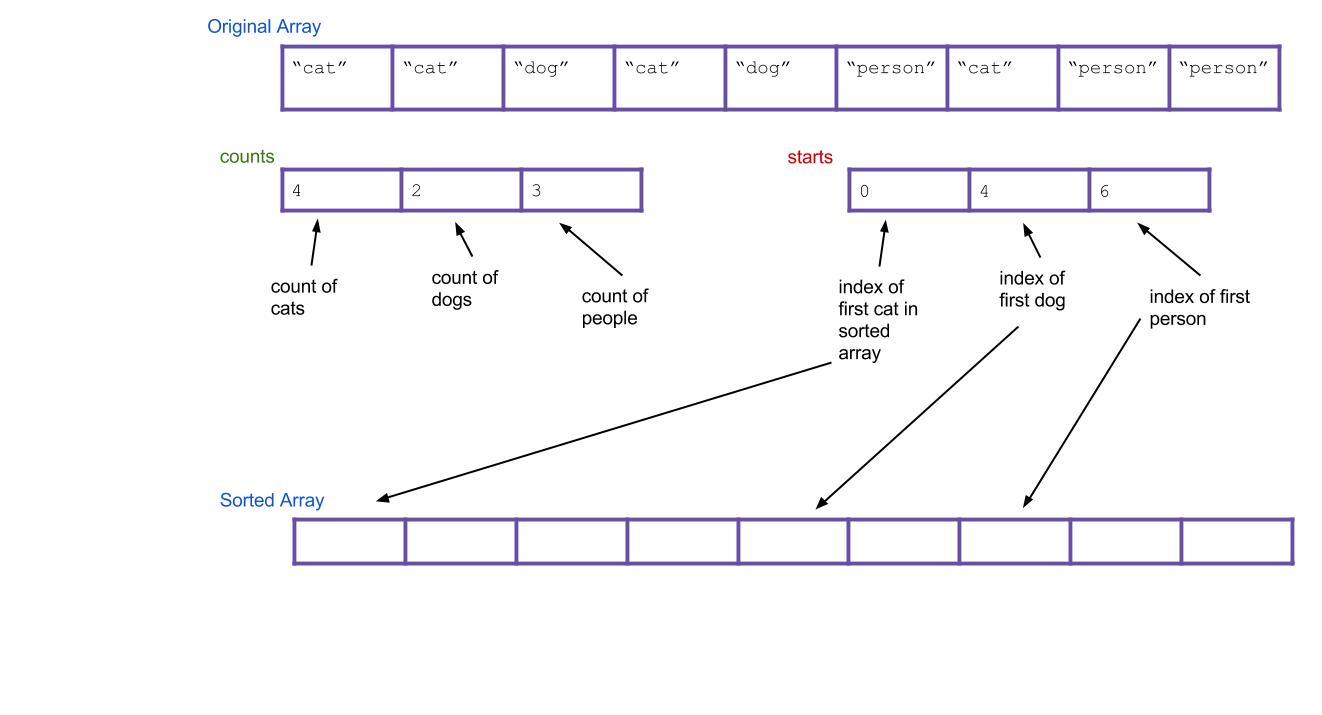
-
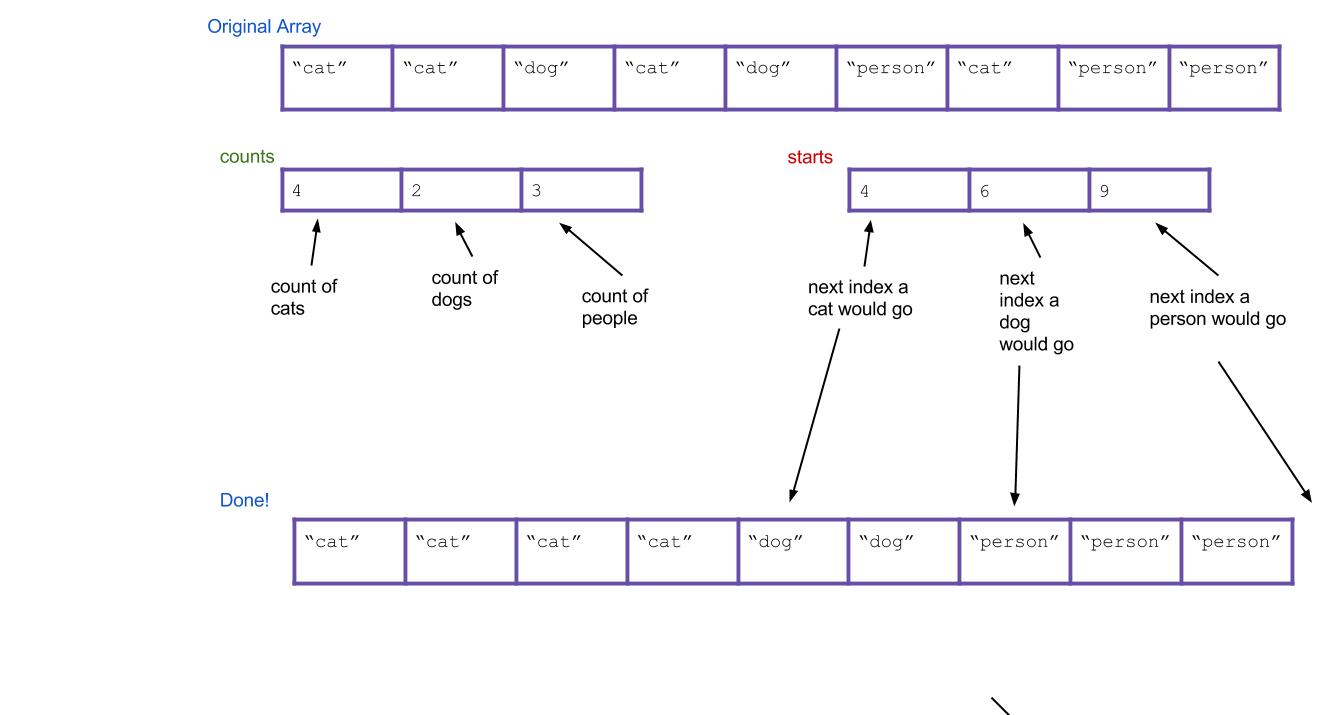
Now iterate through all of our
Strings, and put them into the right spot. When we find the first “cat”, it goes insorted[starts[0]]. When we find the first “dog”, it goes insorted[starts[1]]. What about when we find the second “dog”? It should go insorted[starts[1]+1]! Or, an alternative: we can just incrementstarts[1]every time we put a “dog”. Then, the next “dog” will always go insorted[starts[1]].
Here’s what everything would look like after completing the algorithm. Notice
that the values of starts have been incremented along the way.
This written explanation of counting sort may seem complicated, so it is highly recommended that you take a look at this counting sort visualization before you proceed, as it might make this algorithm more intuitive.
Exercise: Counting Sort #
Exercise 1: countingSort #
Implement the countingSort method in DistributionSorts.java. Assume the only
integers it will receive are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Refer to the above steps if you’re having trouble with this method!
Exercise 2: Runtime #
Inspect the counting sort method you just wrote. What is its runtime? Consider the following two variables:
N: the number of items in the arrayK: the variety of possible items (in the code you wrote,Kis the constant 10, but treat it as a variable for this question).
Discuss with your partner, then highlight the next line for the answer:
N + K .
Runtime: Counting Sort #
Wow, look at that runtime! Does this mean counting sort is a strict improvement from quicksort? Not quite, because counting sort has two major weaknesses:
- It can only be used to sort discrete values. A set of values is discrete if each item is distinct from every other item.
- It will fail if \(K\) is too large, because creating the intermediate
countsarray (of size \(K\)) will be too slow.
The latter point turns out to be a fatal weakness for counting sort. The range of all possible integers in Java is just too large for counting sort to be practical in general circumstances.
Suddenly, counting sort seems completely useless. However, with some modifications that we’ll see in a little bit, we can come up with a pretty good sorting algorithm!
Radix Sort #
Aside from counting sort, all the sorting methods we’ve seen so far are comparison-based, that is, they use comparisons to determine whether two elements are out of order. We also saw the proof that any comparison-based sort needs at least \(\Omega(N \log N)\) comparisons to sort \(N\) elements in the worst case. However, there are sorting methods that don’t depend on comparisons that allow sorting of \(N\) elements in time proportional to \(N\). Counting sort was one, but turned out to be impractical.
However, we now have all the ingredients necessary to describe radix sort, another linear-time non-comparison sort that can be practical.
Let’s first define the word, radix. The radix of a number system is the number of values a single digit can take on (also called the base of a number). Binary numbers form a radix-2 system; decimal notation is radix-10. Radix sorts examine elements in passes, and a radix sort might have one pass for the rightmost digit, one for the next-to-rightmost digit, and so on.
We’ll now describe radix sort in detail. We already described a procedure similar to radix sort when talking about sorting in a library catalog in the last lab. In radix sort, we will pretend each digit is a separate key, and then we sort on all the keys at once, with the higher digits taking precedence over the lower ones.
Here are two good strategies to approach sorting on multiple keys:
- First sort everything on the least important key. Then sort everything on the next key. Continue, until you reach the highest key. Note: This strategy requires the sorts to be stable.
- First sort everything on the high key. Group all the items with the same high key into buckets. Recursively radix sort each bucket on the next highest key. Concatenate your buckets back together.
Here’s an example of using the first strategy. Imagine we have the following numbers we wish to sort:
356, 112, 904, 294, 209, 820, 394, 810
First, we sort them by the first digit:
820, 810, 112, 904, 294, 394, 356, 209
Then we sort them by the second digit, keeping numbers with the same second digit in their order from the previous step:
904, 209, 810, 112, 820, 356, 294, 394
Finally, we sort by the third digit, keeping numbers with the same third digit in their order from the previous step:
112, 209, 294, 356, 394, 810, 820, 904
All done!
Hopefully it’s not hard to see how these can be extended to more than three digits. This strategy is known as LSD radix sort. The second strategy is called MSD radix sort. LSD and MSD stand for least significant digit and most significant digit respectively, reflecting the order in which the digits are considered.
Here’s some pseudocode for the first strategy:
public static void LSDRadixSort(int[] arr) {
for (int d = 0; d < numDigitsInAnInteger; d++) {
stableSortOnDigit(arr, d);
}
}
(the 0th digit is the smallest digit, or the one furthest to the right in the number)
Radix Sort’s Helper Method #
Notice that both LSD and MSD radix sort call another sort as a helper method (in LSD’s case, it must be a stable sort). Which sort should we use for this helper method? Insertion sort? Merge sort? Those would work. However, notice one key property of this helper sort: It only sorts based on a single digit. And a single digit can only take 10 possible values (for radix-10 systems). This means we’re doing a sort where the variety of things to sort is small. Do we know a sort that’s good for this? It’s counting sort! Counting sort turns out to be useful as a helper method to radix sort when it comes to sorting the elements by a particular digit.
Exercise: LSDRadixSort #
Now that you’ve learned what radix sort is, it’s time to try it out yourself. Complete the lsdRadixSort method in DistributionSorts.java by implementing
the countingSortOnDigit method. You won’t be able to reuse your countingSort
from before verbatim because you need a method to do counting sort only
considering one digit, but you will be able to use something very similar.
Disclaimer: Radix sort is commonly implemented at a lower level than base-10, such as with bits (base-2) or bytes (base-16). This is because everything on your computer is represented with bits. Through bit operations, it is quicker to isolate a single bit or byte than to get a base-10 digit. However, because we don’t teach you about bits in this course, you should do your LSD radix sort in base-10 because these types of numbers should be more familiar to you. As you move through the world of computing, you will likely see this referenced in real-world applications of Radix sort!
Runtime: LSD Radix Sort #
To analyze the runtime of radix sort, examine the pseudocode given for LSD radix
sort. From this, we can tell that its runtime is proportional to
numDigitsInAnInteger * (the runtime of stableSortOnDigit).
Let’s call numDigitsInAnInteger the variable \(D\), which is the max number of
digits that an integer in our input array has. Next, remember that we decided
stableSortOnDigit is really counting sort, which has runtime proportional to
\(N + K\), where \(K\) is the number of possible digits, in this case 10. This
means the total runtime of LSD radix sort is \(O(D(N + K))\)!
Discussion: MSD Radix Sort #
Though you will not be implementing MSD Radix sort, understanding how it works is in scope for this course!
To get comfortable, attempt problem 2 from the Spring 2021 Exam Prep 13 Worksheet and watch this video to understand the solution and get a review of MSD radix sort.
With this understanding of how MSD sort works, what is its runtime? How does it differ from LSD radix sort’s runtime? Discuss with your partner.
Hint: Unlike LSD radix sort, it will be important to distinguish best-case and worst-case runtimes for MSD.
Highlight below to see the answer:
Best Case: Theta(N + K) Worst Case: Theta(D(N + K)) .
Advanced Runtime and Radix Selection #
Let’s go back and analyze the LSD radix sort runtime (despite the best-case runtime of MSD radix sort, LSD radix sort is typically better in practice). You may have noticed that there’s a balance between \(K\), the number of digits (also known as the radix), and \(D\), the number of passes needed. In fact, they’re related in this way: let us call \(L\) the length of the longest number in digits. Then \(K \cdot D\) is proportional to \(L\).
For example, let’s say that we have the radix-10 numbers 100, 999, 200, 320. In radix-10, they are all of length 3, and we would require 3 passes of counting sort. However, if we took those same numbers and now use radix-1000, then we examine more of the numbers, all 3 of the base-10 digits, and we only require one pass of counting sort. In fact, in radix-1000, the numbers we used are only of length 1.
In fact, in practice we shouldn’t be using decimal digits at all - radixes are typically a power of two. This is because everything is represented as bits, and as mentioned previously, bit operators are significantly faster than modulo operators, and we can pull out the bits we need if our radix is a power of two.
Without further knowledge of bits, it’s difficult to analyze the runtime further, but we’ll proceed anyways - you can read up on bits on your own time. Suppose our radix is \(K\). Then each pass of counting sort inspects \(\lg K\) bits; if the longest number has b bits, then the number of passes \(D = \frac{b}{\lg K}\). This doesn’t change our runtime of LSD radix sort from \(O(D \cdot (N + K))\).
Here’s the trick: we can choose \(K\) to be larger than in our exercises (10). In fact, let’s choose \(K\) to be in \(O(N)\) (that way each pass counting sort will run in \(O(N)\). We want \(K\) to be large enough to keep the number of passes small. Thus the number of passes needed becomes \(D \in O(\frac{b}{\lg (N)})\).
This means our true runtime must be \(O(N)\) if \(b\) is less than \(\lg N\) or
otherwise \(O(N \cdot \frac{b}{\lg N})\), (plug our choices for \(D\) and \(K\)
into the runtime for LSD radix sort above to see why that’s the case). For very
typical things we might sort, like ints, or longs, \(b\) is a constant, and
thus radix sort is guaranteed linear time. For other types, as long as \(b\) is
in \(O(\lg N)\), this remains in guaranteed linear time. It’s worth noting that
because it takes \(\lg N\) bits to represent N items, this is a very reasonable
model of growth for typical things that might be sorted - as long as your input
is not distributed scarcely.
Conclusion #
Linear-time sorts have their advantages and disadvantages. While they have fantastic speed guarantees theoretically, the overhead associated with a linear time sort means that for input lists of shorter length, low overhead comparison-based sorts like quicksort can perform better in practice. For more specialized mathematical computations, like in geometry, machine learning, and graphics, for example, radix sort finds use.
In modern libraries like Java and Python’s standard library, a new type of sort, TimSort, is used. It’s a hybrid sort between merge sort and insertion sort that also has a linear-time guarantee - if the input data is sorted, or almost sorted, it performs in linear time. In practice, on real-world inputs, it’s shown to be very powerful and has been a staple in standard library comparison sorts.
Deliverables #
To receive credit for this lab:
- Complete the following methods of
DistributionSorts.java:countingSortcountingSortOnDigit
Credit #
Credit to Jonathan Shewchuk for his notes on the lower bound of comparison-based sorting algorithms.
