FAQ #

Each assignment will have an FAQ linked at the top. You can also access it by adding “/faq” to the end of the URL. The FAQ for Lab 11 is located here.

Before You Begin #

As usual, pull the skeleton code.

Learning Goals #

In this lab, you’ll continue to practice coding up binary trees and learn about building data structures that rely on comparisons. This technique will be widely used in the remainder of the class.

Recall: Binary Trees #

We’ll now move on from trees and explore a common, special case of the tree data structure: the binary tree. A binary tree is a tree in which each node has at most two children. Normally it has two separate variables left and right for the left and right children of the binary tree.

Exercise: BinaryTree #

The file BinaryTree.java defines a BinaryTree class and a TreeNode class. First, read over the code, as well as the implementations for printPreorder and printInorder.

Then, read over methods that generate sample trees (sampleTreeX methods) and try running the main method to understand how it works. In addition, consider adding more test cases to the BinaryTreeTest.java.

Once you have understood the code, you can start working on the exercises below.

Exercise 1: height #

First, if you have a partner, switch which partner is coding if you haven’t recently.

Implement the height method in the BinaryTree class. The height of an empty tree is 0; the height of a one-node tree is 1; the height of any other tree is 1 + the greater of the heights of the two children.

Exercise 2: isCompletelyBalanced #

Add an isCompletelyBalanced method for the BinaryTree class. A tree with no nodes and a tree with one node are both completely balanced; any other tree is completely balanced if and only if the height of its left child is equal to the height of its right child, and its left and right children are also completely balanced. Make sure you test your code with trees of height 3 or more to ensure that your code works!

Exercise 3: fibTree #

This exercise deals with “Fibonacci trees”, trees that represents the recursive call structure of the Fibonacci computation. (The Fibonacci sequence is defined as follows: \(F_0 = 0, F_1 = 1\), and each subsequent number in the sequence is the sum of the previous two.) The root of a Fibonacci tree should contain the value of the Nth Fibonacci number, the left subtree should be the tree representing the computation of the N-1th Fibonacci number, and the right subtree should be the tree representing the computation of the N-2th Fibonacci number. The two exceptions to this rule are when we pass in 0 or 1 to the fibTree method. The first few Fibonacci trees appear below.

Function	Tree
fibtree(0)
fibtree(1)
fibtree(2)
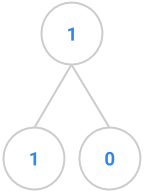fibtree(3)
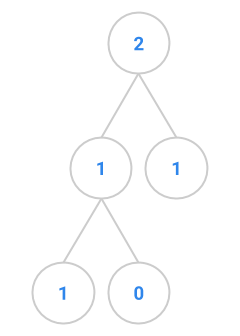fibtree(4)
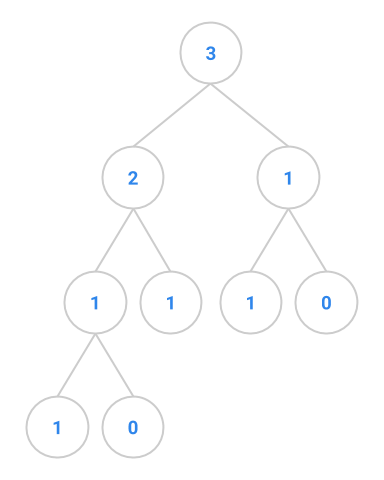fibtree(5)

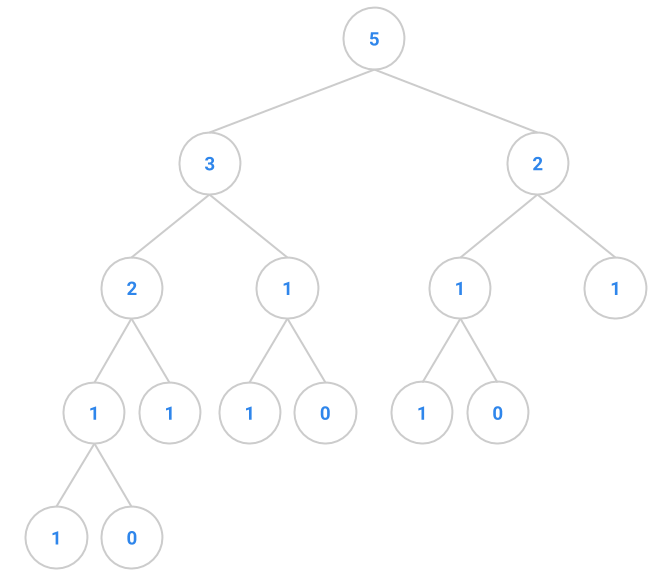Write the static fibTree method in BinaryTree that takes in a non-negative integer N, and returns a BinaryTree that stores the N-th Fibonacci value using the representation above.

You should be using recursion for these problems, and you should be adding your helper methods with modified arguments. Refer to the tree traversal code for reference!

Furthermore, because fibTree is a static method that returns a BinaryTree, your helper method must be static as well!

Comparisons #

Here are a few key details from compareTo, slightly adapted:

Compares this object with the specified object for order. Returns a negative integer or a positive integer if this object is less than or greater than the specified object, respectively. Note that it can be any negative or positive integer, not -1 and 1 necessarily.

There are other requirements that usually just happen naturally with a reasonable implementation, but are still important to specify:

The implementer must also ensure that the relation is transitive: x.compareTo(y) > 0 && y.compareTo(z) > 0 implies x.compareTo(z) > 0.

It is strongly recommended, but not strictly required that x.compareTo(y) == 0 is equivalent to x.equals(y). Generally speaking, any class that implements the Comparable interface and violates this condition should clearly indicate this fact. The recommended language is “Note: this class has a natural ordering that is inconsistent with equals.”

Typically, a class will compare to objects of the same type as itself (although it does not strictly have to). Doing so means data structures that require ordering (like sorted lists, and in the future, search trees) can contain the class.

Binary Search #

Suppose we have a sorted array of comparable elements, and we want to see if a certain element is in the array. How can we use compareTo() to achieve an efficient implementation? Before reading the next section, pause here and discuss approaches with your peers!

We can employ the well known divide-and-conquer algorithm known as binary search. Used with an array where low, mid, and high are array indices, binary search assumes that the elements of the array are sorted in increasing order, and executes the following:

1. Set low to 0 and high to the length of the array minus 1. The value we’re looking for — we’ll call it k— will be somewhere between position low and position high if it’s in the array.
2. While low \(\leq\) high, do one of the following:
   • Compute mid, the middle of the range [low, high], and see if that’s k. If so, return true.
   • Otherwise, we can cut the range of possible positions for k in half, by setting high to mid - 1 or by setting low to mid + 1, depending on the result of the comparison.
3. If the loop terminates with low > high, we know that k is not in the array, so we return **false.

The diagrams below portray a search if k was equal to 25. Elements removed from consideration at each iteration are greyed out.

low = 0, mid = 7, high = 14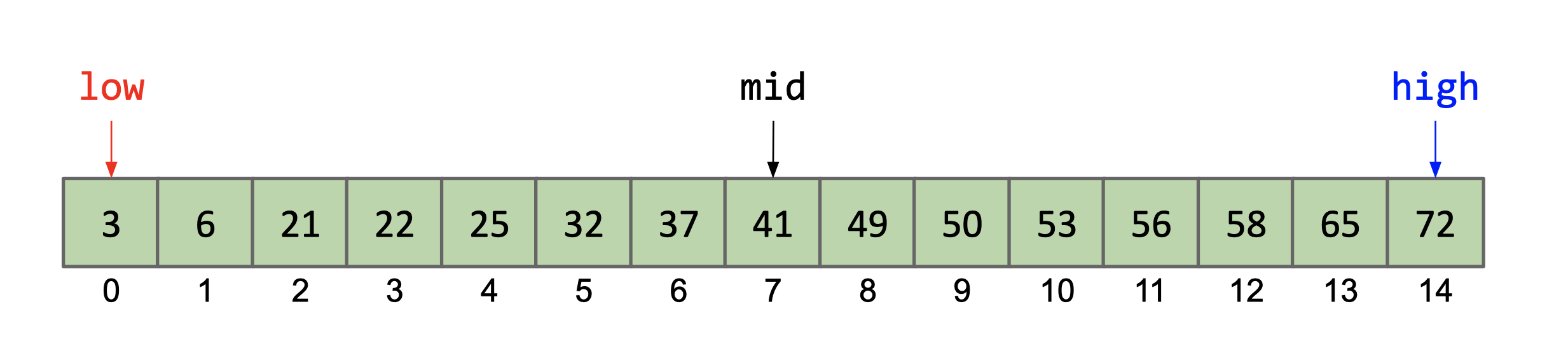

low = 0, mid = 3, high = 6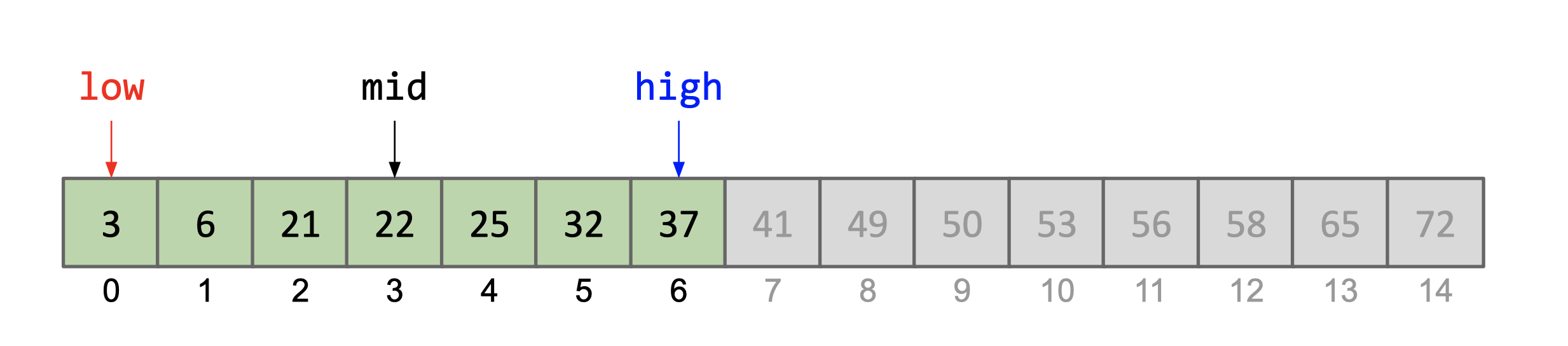

low = 4, mid = 5, high = 6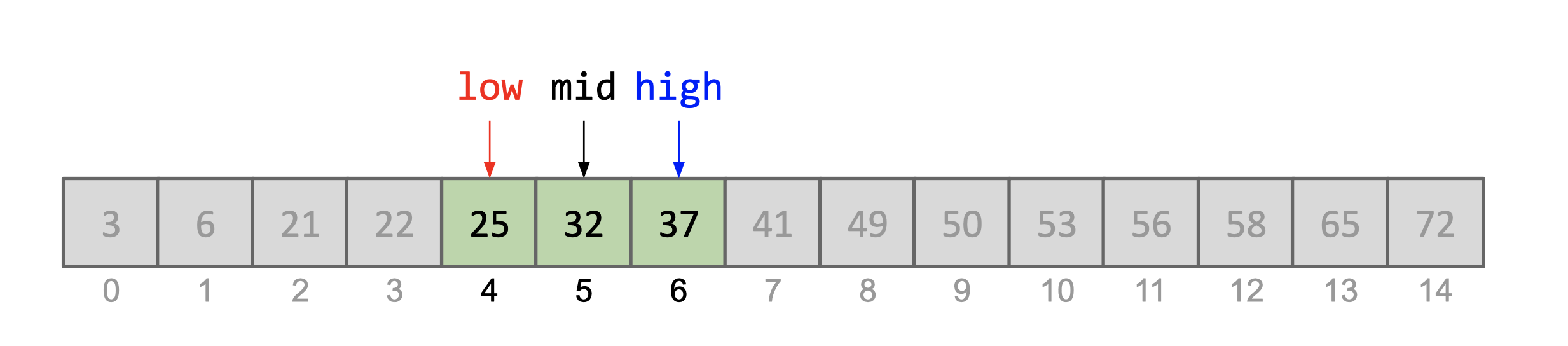

low = 4, mid = 4, high = 4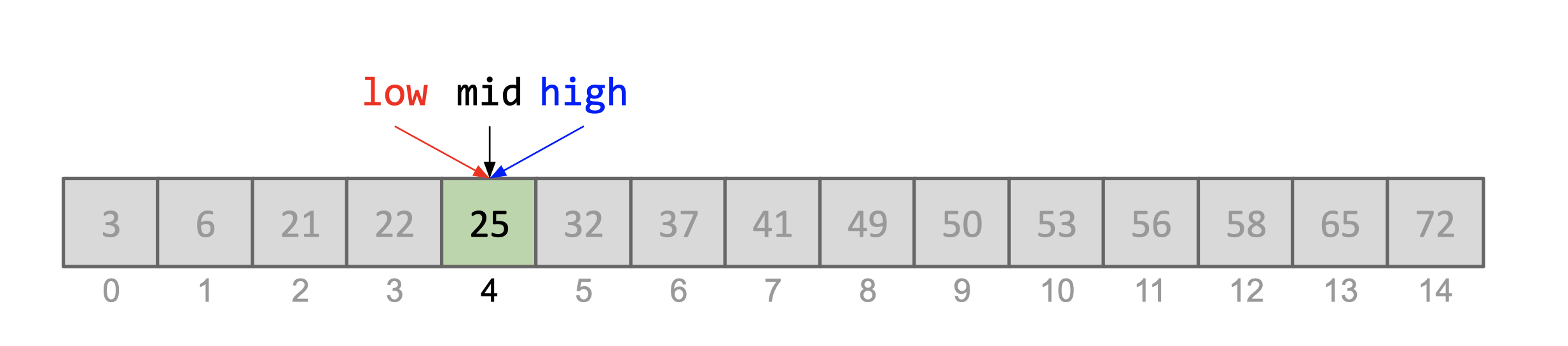

What would be the worst case running time of a search for k? Highlight the next line for the answer after discussing with your peers:

Since (roughly) half the elements are removed from consideration at each step, the worst-case running time is proportional to log_2(N), where N is the number of elements in the array..

Binary Search Trees #

The binary search algorithm suggests a way to organize keys in an explicitly linked tree, as indicated in the diagram below.

Notice that as we searched for 25 in the example above, we essentially traversed this tree from 41 to 25!

The data structure that results is called a binary search tree (BST). Given that the root value (one of the keys to be stored) is \(k\), a binary search tree is organized as follows:

• Put all the keys that are smaller than \(k\) into a binary search tree, and let that tree be \(k\)’s left subtree.
• Put all the keys that are larger than \(k\) into a binary search tree, and let that tree be \(k\)’s right subtree.

This organization assumes that there are no duplicate keys among those to be stored.

contains #

It’s important to note that in a binary search tree, each subtree is also a binary search tree. This suggests a recursive rather than an iterative approach for implementing many methods and the contains method is no different. In pseudocode, here is an outline of the helper method of the contains method, containsHelper(TreeNode t, T key):

1. An empty tree cannot contain anything, so if t is null return false.
2. If key is equal to t.item, return true.
3. If key < t.item, key must be in the left subtree if it’s in the BST at all, so return the result of searching for it in the left subtree.
4. Otherwise it must be in the right subtree, so return the result of searching for key in the right subtree.

Note: that the type of key is T, which is the generic type of the BinaryTree class.

This algorithm can go all the way down to a leaf to determine its answer. Thus in the worst case, the number of comparisons is proportional to \(d\), the depth of the tree. In a balanced tree (more on that next lab), you can expect the depth of the tree to be proportional to \(\log N\) in the worst case, where \(N\) is the number of nodes in the tree.

Use of Comparable objects #

Finding a value in the tree will require “less than”, “greater than”, and “equals” comparisons. Since the operators < and > don’t work with objects, we have to use method calls for comparisons.

The Java convention for this situation is to have the values stored in the tree be objects that implement the Comparable interface, which you learned about in lab 8.

Balance and Imbalance #

Unfortunately, the use of a binary search tree does not guarantee efficient search.

What would be the worst case runtime possible for a single call to contains() on a valid BST? Discuss with your peers and highlight the next line for the answer.

Θ(n) .

For example, the tree

is a binary search tree in which search proceeds in the same runtime as a linked list. We thus are forced to consider the balance of a binary search tree. Informally, a balanced tree has subtrees that are roughly equal in size and depth. Next lab, we will encounter specific algorithms for maintaining balance in a binary search tree. Until then, we will work under the possibly unwarranted assumption that we don’t need to worry much about balance.

One can prove (optional to read, but an important fact to know), incidentally, that search in a BST of \(\)N\(\) keys will require only about \(\)2 \ln N\(\) comparisons (where \(\)\ln\(\) is the “natural log” of \(\)N\(\)) if the keys are inserted in random order. Well-balanced trees are common, and degenerate trees are rare.

Insertion into a BST #

If we have 4 nodes in our binary search tree, there are actually 14 different BST’s you could make. Correspondingly, there are typically a bunch of places in a BST that a key to be inserted might go, anywhere from the root down to a leaf. Given below are two trees; the tree on the right shows one possible way to insert the key 41 into the tree on the left.

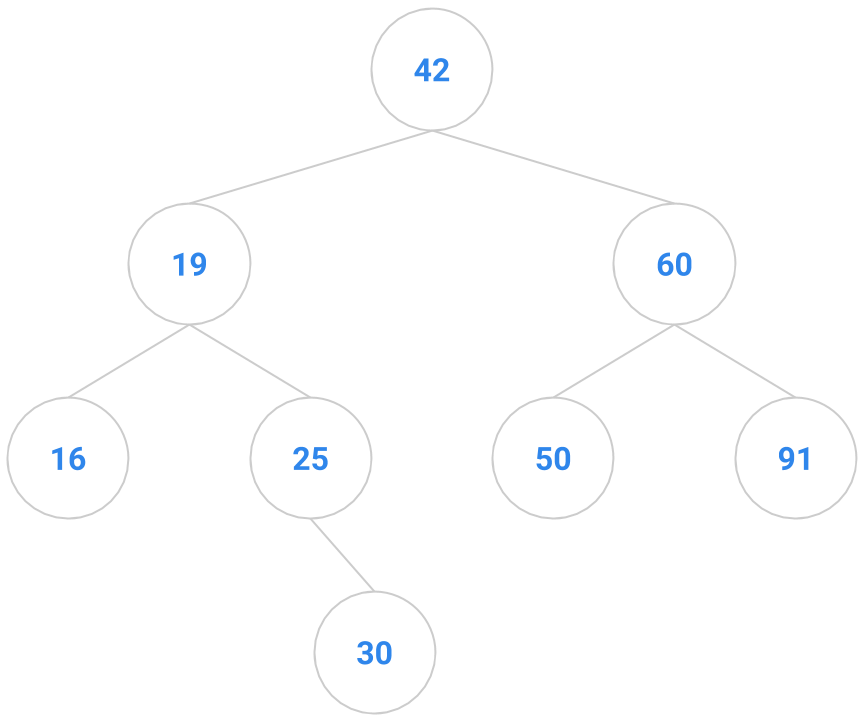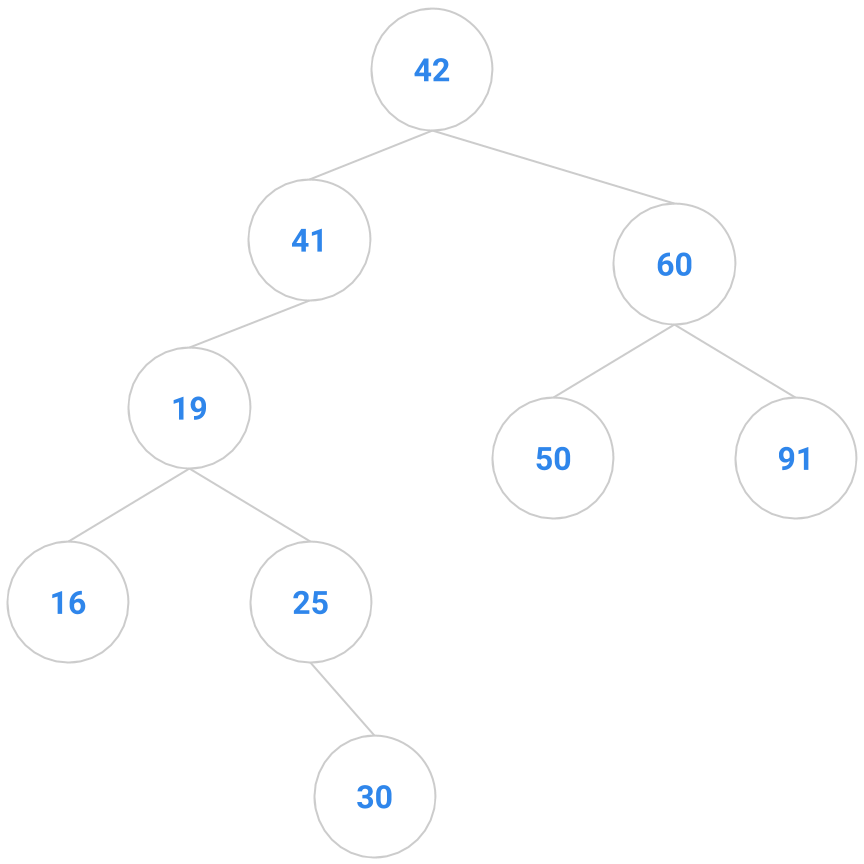However, to minimize restructuring of the tree and the creation of internal nodes, we choose in the following exercise to insert a new key only as a new leaf.

USFCA put together a BST visualization interactive animation to help you visualize the BST insertion and deletion algorithms. Try inserting a key that ends up as a right child and another key that ends up as a left child. Add some more nodes to the tree, then delete some of them: a node with no children, a node with one child, and a node with two children.

Note that this animation deletes from the BST by swapping with the inorder predecessor rather than the inorder successor. Convince your peers that this is essentially equivalent.

Exercises: BST Implementation #

Now it’s time to start writing code! As you go, don’t forget to write JUnit tests.

Since binary search trees share many of the characteristics of regular binary trees, we can define the BinarySearchTree class using inheritance from a provided BinaryTree class.

Exercise 1: Testing Utilities #

As always, we will start by ensuring our ability to test our code. In BinaryTree.java, you can find a print() method that serves as the foundation for BinaryTreeTest.java. Any test run right now will fail, because printInorder() has not been implemented.

Implement both:

/* Print the values in the tree in inorder. */
public void printInorder() {

in BinaryTree and

/* Prints the nodes of the BinaryTree in inorder. Used for your testing. */
private void printInorder() {

in BinaryTree.TreeNode to allow for our tests to function.

Binary Search Tree #

The BinarySearchTree class is defined as follows:

public class BinarySearchTree<T extends Comparable<T>> extends BinaryTree<T>

This class definition is a slightly more complicated use of generic types than you have seen before in lab. Previously, you saw things like BinaryTree<T>, which meant that the BinaryTree class had a generic type T that could be any class, interface, or abstract class that extends Object. In this case, BinarySearchTree<T extends Comparable<T>> means that the BinarySearchTree class has a generic type T that can be any class, interface, or abstract class that implements the Comparable<T> interface. In this case, Comparable<T> is used because the Comparable interface itself uses generic types (much like the Iterable and Iterator interfaces).

Take a look through the BinarySearchTree and BinaryTree classes, and familiarize yourself with the methods that are available to you.

Exercise 2: contains #

Now, we will implement the contains method. We will use the following method signature:

public boolean contains(T key)

which takes a Comparable object T as an argument and checks whether the tree contains it.

Recall that Comparable objects provide an int compareTo method that returns:

• a negative integer if this object is less than the argument,
• a positive integer if this object is greater than the argument, and
• 0 if the two objects have equal values.

Depending on whether you take a recursive or iterative approach, you may need to define a helper method. If you’re stuck, take a look at the pseudocode that we described above!

Exercise 3: add #

We will now define an add method. We will use the following method signature:

public void add(T key)

which takes a Comparable object as an argument and adds it to the tree if and only if it isn’t already there. The trees you create with the add method will thus not contain any duplicate elements.

Hint: You should be able to do this in a similar way to the contains method. When you’re done with both, you can write a JUnit test suite to test your code. Don’t forget edge cases!

Optional Exercise 4: Optional Constructor #

For additional practice constructing Binary Trees, implement

public BinaryTree(ArrayList<T> pre,  ArrayList<T> in)

which constructs a Binary Tree given the preorder traversal (pre) and inorder traversal (in) provided as ArrayList arguments in BinaryTree.java. We recommend a recursive approach.

Discussion: BST Deletion #

We’ve covered adding to a BST and contains in a BST. But how about deletion?

When inserting a key, we were allowed to choose where in the tree it should go. The deletion operation doesn’t appear to allow us that flexibility; deletion of some keys will be easy (leaves or keys with only one child), but our deletion method has to be able to delete any key from the tree.

Here are a bunch of binary search trees that might result from deleting the root of the tree

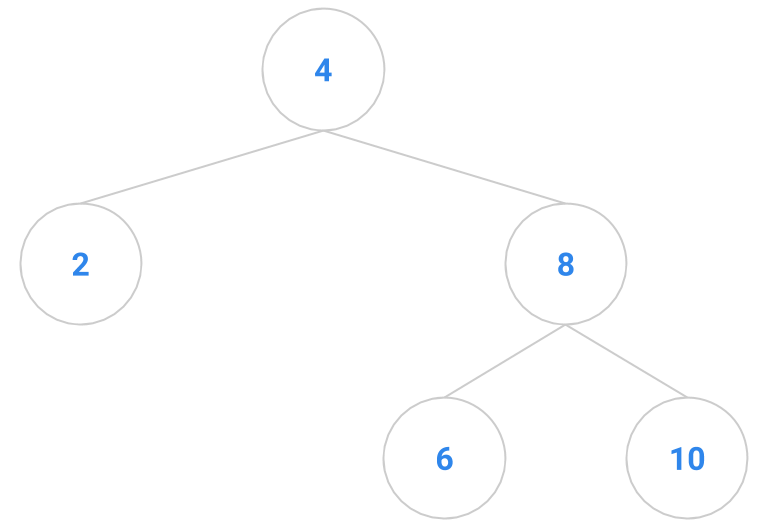
Which ones do you think are reasonable?

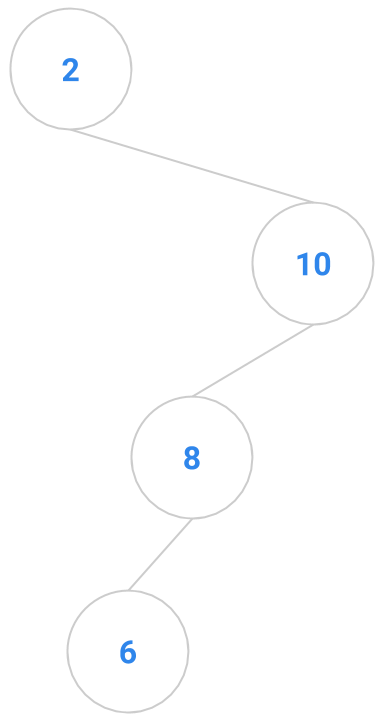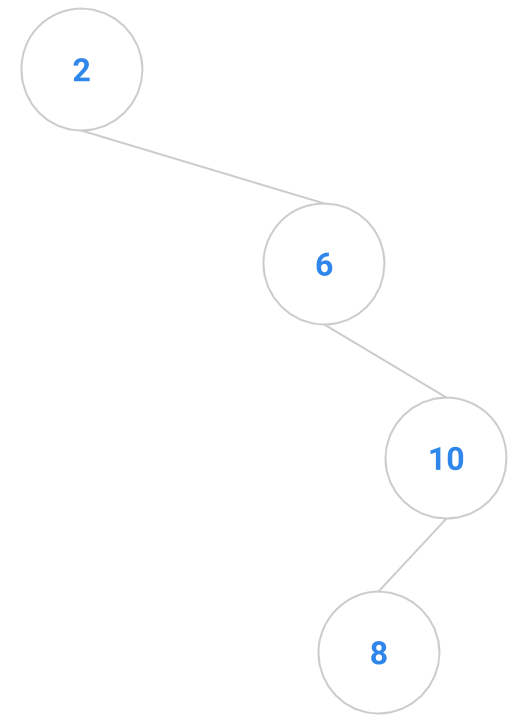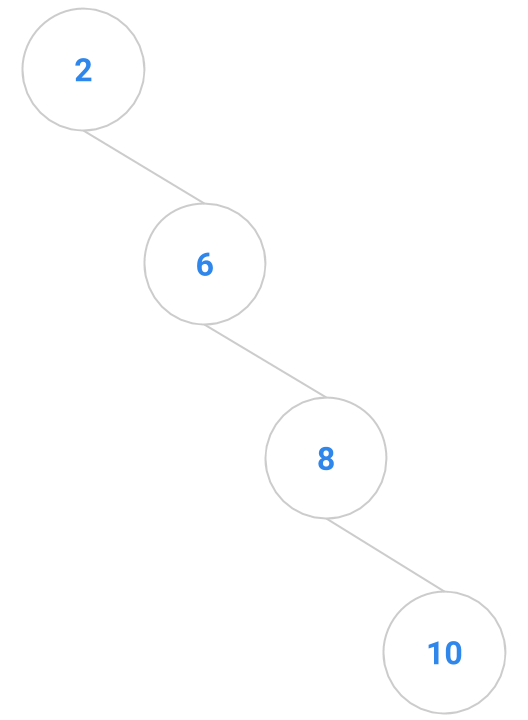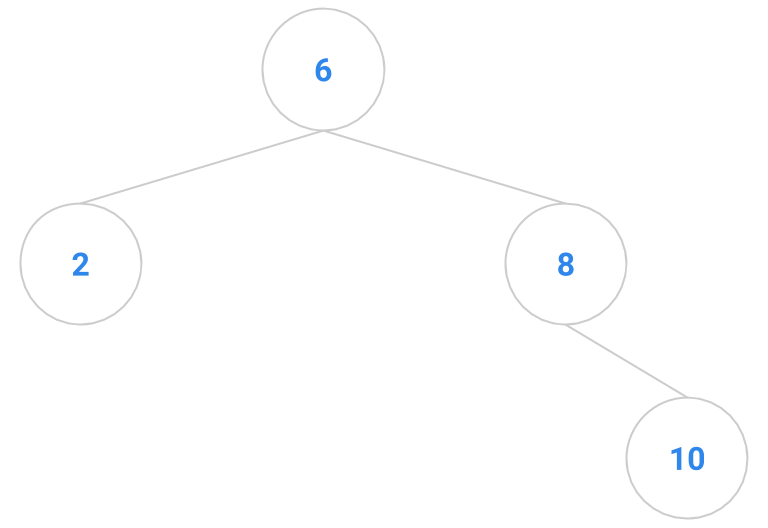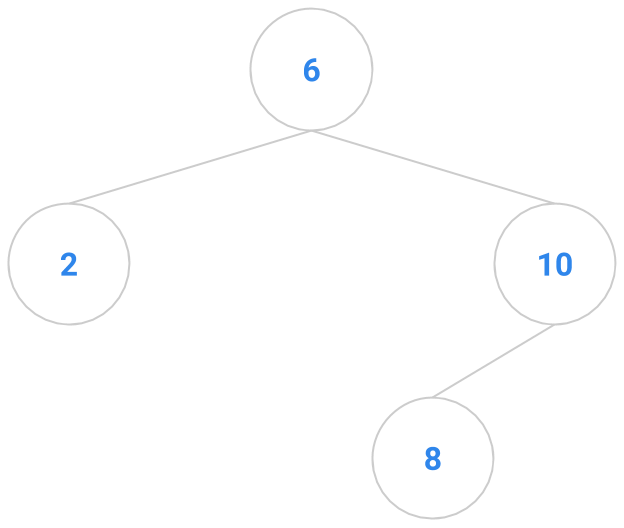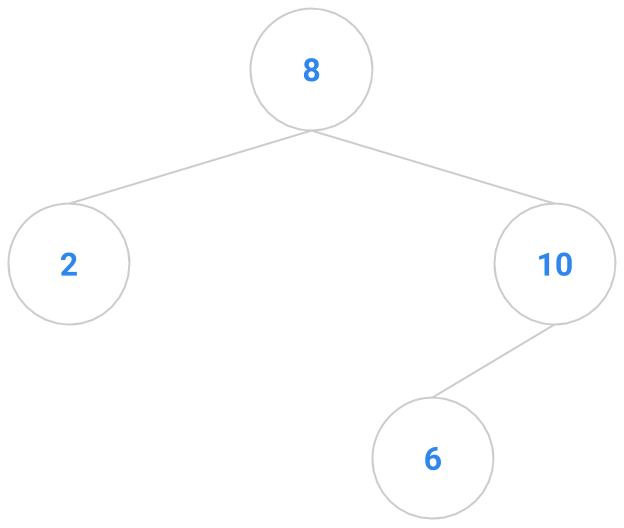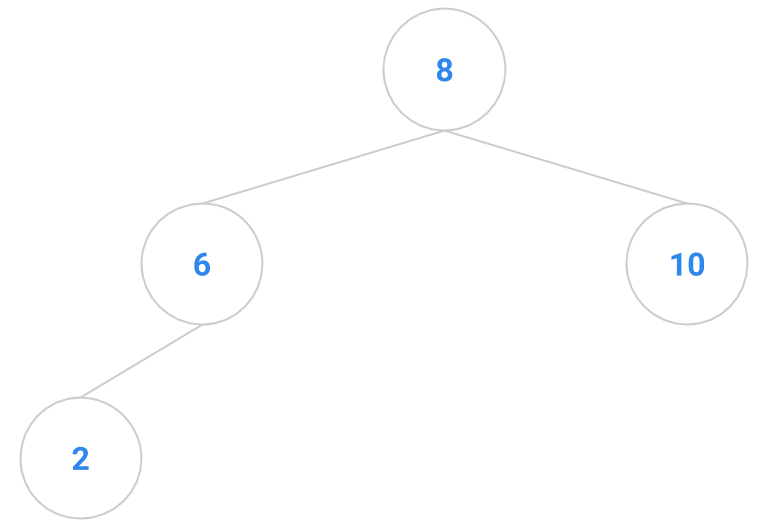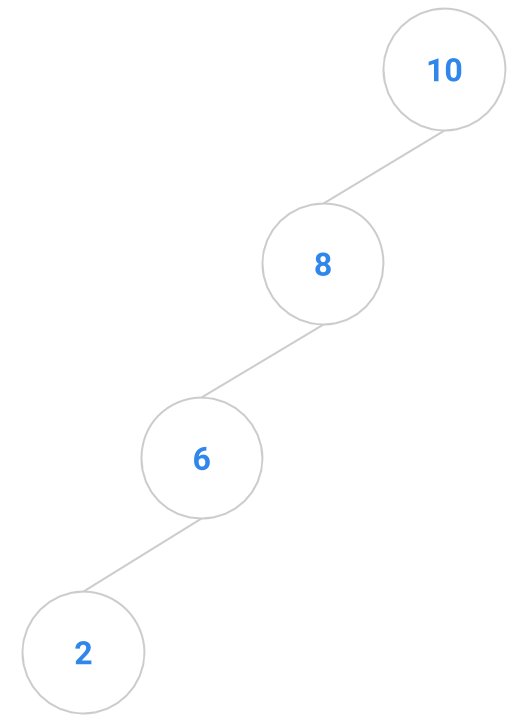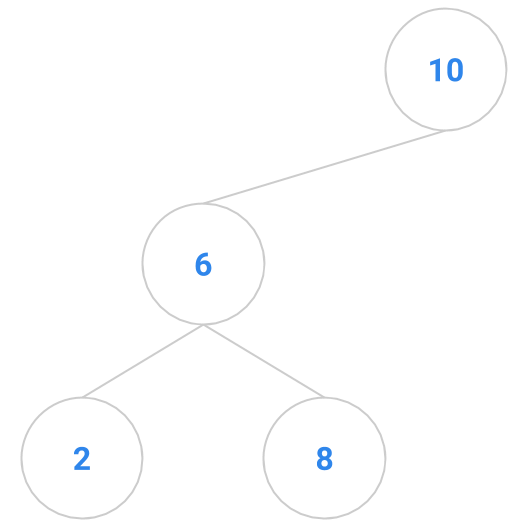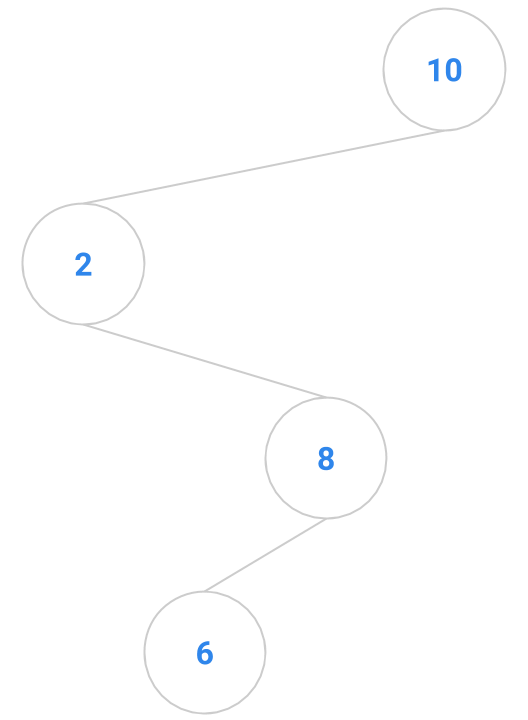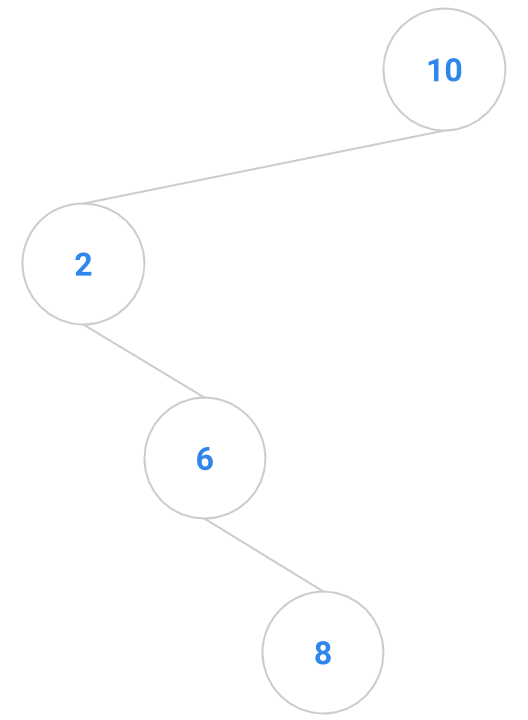A Good Way to Delete a Key #

The following algorithm for deletion has the advantage of minimizing restructuring and unbalancing of the tree. The method returns the tree that results from the removal.

1. Find the node to be removed. We’ll call it remNode. If it’s a leaf, remove it immediately by returning null. If it has only one child, remove it by returning the other child node.
2. Otherwise, remove the inorder successor of remNode OR remove the inorder predecessor, copy its item into remNode, and return remNode.

What is an inorder successor? It is the node that would appear AFTER the remNode if you were to do an inorder traversal of the tree.

An example is diagrammed below. The node to remove is the node containing 4. It has two children, so it’s not an easy node to remove. We locate the node with 4’s inorder successor, namely 5. The node containing 5 has no children, so it’s easy to delete. We copy the 5 into the node that formerly contained 4, and delete the node that originally contained 5.

Before	After

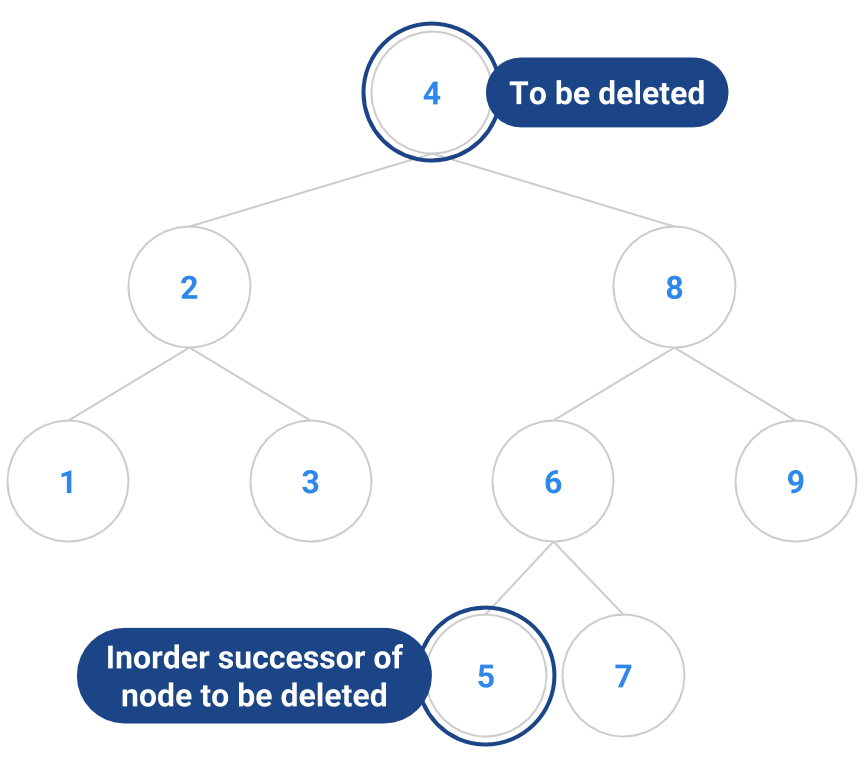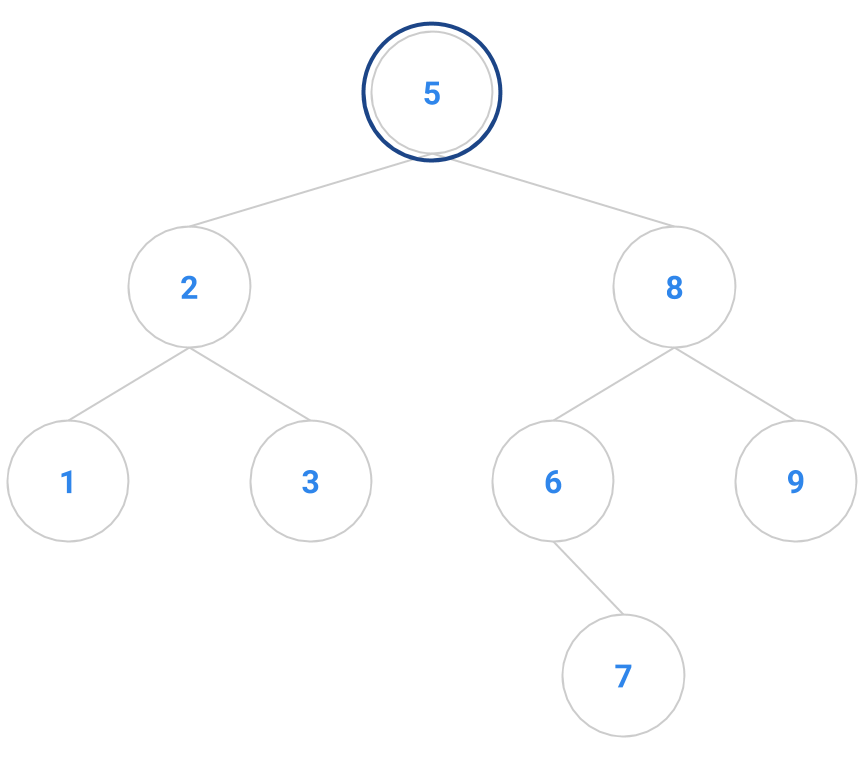Inorder Successor #

Suppose node is the root node in a BST with both a left child and a right child. Will sucNode, the inorder successor of node, ALWAYS have a null left child? Discuss this with your peers.

We’ve implemented a delete method for you already. Take a look at it and understand how it works.

The Engineer’s Tradeoff #

Consider the problem of finding the kth largest key in a binary search tree. An obvious way of doing this is to use the inorder enumeration from this week’s lab; we could call nextElement until we get the desired key. If k is near the number of keys N in the tree, however, that algorithm’s running time is proportional to N. We’d like to do better. But how?

If you haven’t yet noticed, this class is all about tradeoffs—finding the delicate balance between two conflicting factors to perfectly suit a certain task. Choosing an appropriate data structure is one tradeoff: an algorithm that requires quick access to a certain piece of information would perform better on an array, but an algorithm that uses many insert and delete operations would probably do better in a linked list. Sacrificing a shorter running time in exchange for more memory space, or vice versa, is another.

For this problem, we can reduce the runtime of the kth largest key by storing in each node the size of the tree rooted at that node. Can you design an algorithm using this idea that runs in time proportional to d, where d is the depth of the tree?

Deliverables #

Here’s a quick recap of what you need to do to complete this lab!

• Complete the following methods in BinaryTree.java:
  • height()
  • isCompletelyBalanced()
  • fibTree(int N)
• Complete the following methods in BinarySearchTree.java:
  • contains(T key)
  • add(T key)
• Understand the delete method of the BinarySearchTree.

Submit all of these to Gradescope.