FAQ #

Each assignment will have an FAQ linked at the top. You can also access it by adding “/faq” to the end of the URL. The FAQ for Lab 19 is located here.

Before You Begin #

As usual, pull the files from the skeleton and make a new IntelliJ project.

Minimum Spanning Tree #

Consider an undirected graph \(G = (V,E)\) comprising of a set of vertices, \(V\), and a set of edges, \(E\). Let’s define some terms first:

A tree is a connected graph that has no cycles. If it has \(N\) vertices, then it must have exactly \(N - 1\) edges in order to satisfy these properties.

A spanning tree, informally, can be thought of as a tree that spans all the vertices in a graph. Formally, a spanning tree \(T = (V, F)\) of \(G\) is a tree that contains all of the vertices \(V\) of the graph \(G\), and a subset of its edges: \(F \subseteq E\), where \(|F| = |V| - 1\).

Here’s an example of two different spanning trees on the same graph. Notice how each spanning tree contains all of the vertices \(V\) in the graph, exactly \(|V| - 1\) edges, and is connected. Because the original graph \(G\) may have many other edges, it’s possible for there to exist multiple spanning trees.

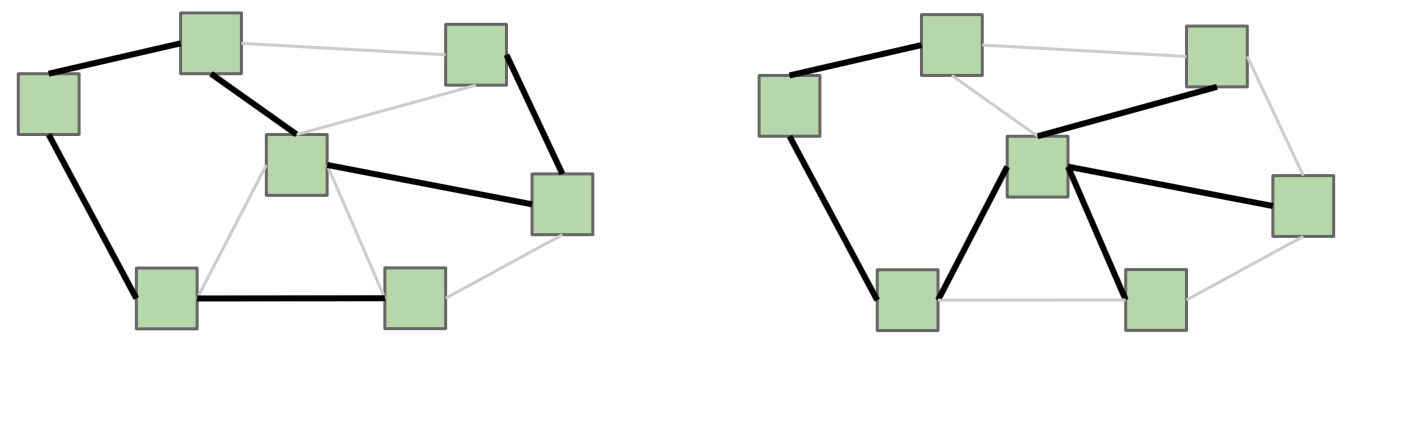
A minimum spanning tree (MST for short) \(T\) of a weighted undirected graph \(G\) is a spanning tree where the total weight (the sum of all of the weights of the edges) is minimal. That is, no other spanning tree of \(G\) has a strictly smaller total weight. The MST for a graph is not necessarily unique.

Consider the graph below. Which edge is not in the MST of this graph? Discuss with your partner.

\[\overline{AB}, \overline{AD}, \overline{BD}, \overline{DC}\]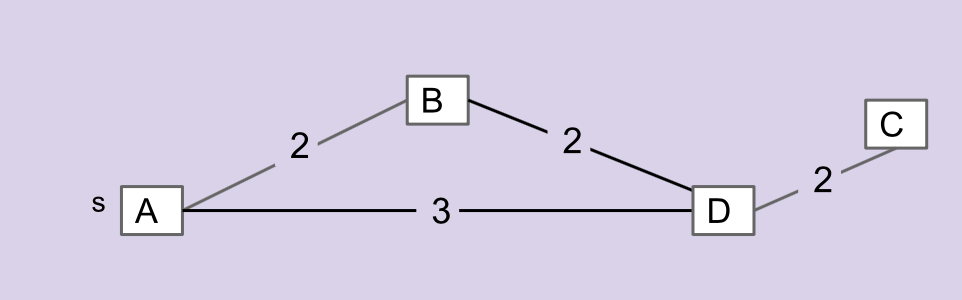

Answer (click to reveal):

The edge \(\overline{AD}\) is not in the MST. The MST contains the other three edges.

Cut Property #

Before we go into specific algorithms for finding MSTs, let’s talk about a property that helps find them. To talk about this, we will need to define a few more terms:

• Cut: an assignment of a graph’s vertices into two non-empty sets
• Crossing edge: an edge which connects a vertex from one set to a vertex from the other set

Examples of the above can be found in the graph below, where the two sets making up the cut are the set of white vertices and the set of gray vertices:

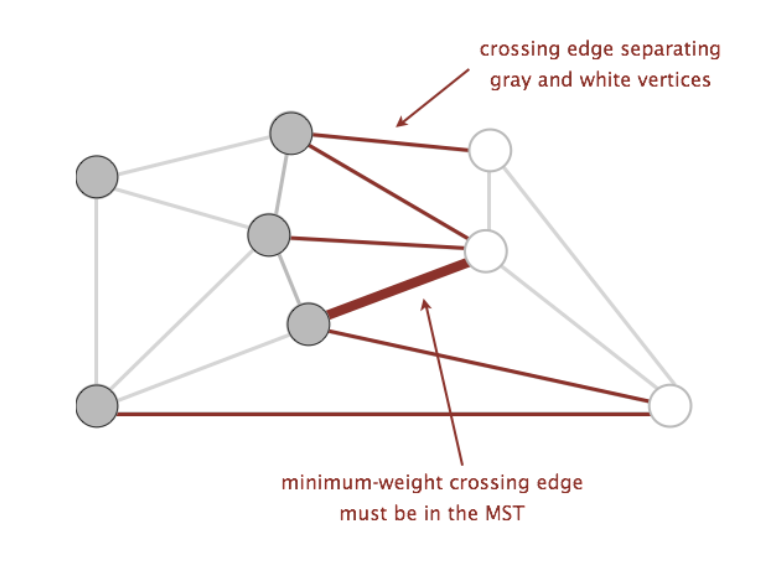
Sedgewick’s Algorithms, 4th Ed.

Using these two terms, we can define a new property called the cut property. The cut property states that given any cut of a graph, the crossing edge with the smallest weight is in all MSTs. If multiple crossing edges have the same minimum weight, then each of these edges is in some MST.

We omit the proof in this class, as you’ll learn more about proofs in CS (1)70. If you’re interested, Wikipedia has a very short summary.

The question is now, what cuts of the graph do we use to find the minimum weight crossing edges to add to our MST? Random cuts may not be the best way to approach this problem. We’ll discuss the following algorithms that choose the cuts to consider in their own way: Prim’s algorithm and Kruskal’s algorithm.

Prim’s Algorithm #

Prim’s algorithm is a greedy algorithm that constructs an MST, \(T\), from some graph \(G\) as follows:

1. Create a new empty graph \(T\), where \(T\) will be the resulting MST.
2. Choose an arbitrary starting vertex in graph \(G\) and add that vertex to graph \(T\).
3. Repeatedly add the smallest edge of graph \(G\), that has exactly one vertex inside graph \(T\) to \(T\). Let’s call this edge \(e\). After adding edge \(e\), we will also add the vertex on edge \(e\) that is not in graph \(T\) to \(T\).
4. Continue until graph \(T\) has \(V - 1\) edges.

Now, why does Prim’s algorithm work? The answer is the cut property. At any given point in the algorithm, the two sets of vertices that make up the cut are:

• vertices of \(T\)
• vertices of \(G\) that aren’t in \(T\)

\(e\) is the smallest crossing edge between \(T\) and a vertex not in \(T\). Since Prim’s always adds the minimum crossing edge, by the cut property, each edge that it adds is a part of an MST. Since we only add those edges, we have created a valid MST!

Now, how do we implement this algorithm? We will just need a way to keep track of what \(e\) is at any given time. Because we always care about (only) the minimum, we can use a priority queue!

The priority queue will contain all vertices that are not part of \(T\), and the priority value of a particular vertex \(v\) will be the weight of the shortest edge that connects \(v\) to \(T\). At the beginning of every iteration, we will remove the vertex \(u\) whose connecting edge to \(T\) has the smallest weight, and add the corresponding edge to \(T\). Adding \(u\) to \(T\) will grow our MST, meaning that there will be more edges to consider that have one vertex in \(T\) and the other vertex not in \(T\). For each of these edges \((u, w)\), if this edge has smaller weight than the current edge that would connect \(w\) to \(T\), then we will update \(w\)’s priority value to be the weight of edge \((u, w)\).

Does this procedure sound familiar? Prim’s algorithm actually bears many similarities to Dijkstra’s algorithm, except that Dijkstra’s uses the distance from the start vertex rather than the distance from the MST as the priority values in the priority queue. However, due to Prim’s algorithm’s similarity to Dijkstra’s algorithm, the runtime of Prim’s algorithm will be exactly the same as Dijkstra’s algorithm!

To see a visual demonstration of Prim’s algorithm, see the Prim’s Demo.

Exercise: Prim’s Algorithm #

Before we implement Prim’s algorithm, let’s familiarize ourselves with the graph implementation for this lab.

Graph Representation #

Graph.java and Edge.java will define the Graph API we will use for this lab. It’s a bit different from previous labs, so we will spend a little time discussing its implementation. In this lab, our graph will represent vertices with integers, and edges with instances of the Edge class. Vertices are numbered starting from 0, so a Graph instance with \(N\) vertices will have vertices numbered from 0 to \(N - 1\). A Graph instance maintains three instance variables:

• neighbors: a HashMap mapping vertices to a set of their neighboring vertices.
• edges: a HashMap mapping vertices to their adjacent edges.
• allEdges: a TreeSet of all the edges present in the current graph.

A Graph instance also has a number of instance methods that may prove useful. Read the documentation to get a better understanding of what each does!

prims #

Now, fill in the prims method of the Graph class. You may want to refer back to your code for Dijkstra’s algorithm from Lab 18 for inspiration. Keep in mind the different graph representation that we have for this lab.

Hint: Whenever we pop a vertex \(v\) off the fringe, we want to add the corresponding Edge object that connects \(v\) to the MST that we are constructing. This means that we should keep a mapping between vertex number \(i\) and the Edge object with minimum weight that connects vertex \(i\) to the MST. Consider maintaining a map called distFromTree that will keep this mapping between integers (vertex numbers) and Edge objects.

Handling Edge Cases in prims #

Sometimes, a graph may not have a minimum spanning tree. For example, if the graph is not connected, then there is no way to create a spanning tree that includes all vertices. In this case, the prims method should return null.

Try running Prim’s on the graph below, and see what happens!

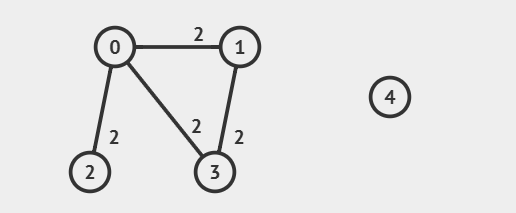
Recall how Prim only explores along existing edges. If there are no more edges to explore, then the while (fringe is not empty) condition does not hold. Now, consider checking the number of edges in your MST. Typically, a graph with \(V\) vertices will have \(V - 1\) edges in its MST. If so, under what conditions can we say it’s not possible to find the MST?

Testing #

To test the code that you have just written, we have included a directory named inputs and a few methods that will help generate test graphs. The inputs directory contains text documents which can be read in by Graph.java to create a new graph. The syntax for the input files is as follows:

# Each line defines a new edge in the graph. The format for each line is
# fromVertex, toVertex, weight
0, 1, 3
1, 2, 2
0, 2, 1

This document creates a graph with three edges. One from vertex 0 to 1 with weight 3, one from 1 to 2 with weight 2, and one from 0 to 2 with weight 1. You may optionally have your text file only add vertices into the graph. This can be done by having each line contain one number representing the vertex you want to add.

# Start of the file.
0
4
2

This creates the graph with vertices 0, 4, and 2. You can define and use your own test inputs by creating a file, placing it into inputs and then reading it in using Graph.loadFromText!

Kruskal’s Algorithm #

Let’s discuss the second algorithm, Kruskal’s algorithm, another greedy algorithm that can calculate the MST of \(G\). It goes as follows:

1. Create a new graph \(T\) with the same vertices as \(G\), but no edges (yet).
2. Make a list of all the edges in \(G\).
3. Sort the edges from smallest weight to largest weight.
4. Iterate through the edges in sorted order. For each edge \((u, w)\), if \(u\) and \(w\) are not connected by a path in \(T\), add \((u, w)\) to \(T\).

What are the cuts for this algorithm? For Kruskal’s algorithm, the cut will be made by the following sets of vertices:

• vertices of \(T\) connected by any edge
• vertices of \(T\) not connected by any edge

Because Kruskal’s algorithm never adds an edge that connects vertices \(u\) and \(w\) if there is a path that already connects the two, \(T\) is going to be a tree. Additionally, we will be processing the vertices in sorted order, so if we come across an edge that crosses the cut, then we know that that edge will be the minimum weight edge that crosses the cut. Continually building our tree in this way will result in building the MST of the original graph \(G\).

Both Prim’s and Kruskal’s are greedy algorithms, but in different ways. Discuss the commonalities and important distinctions between the two algorithms with your partner.

Exercise: Kruskal’s Runtime #

Exercise 1: Using a Traversal #

How about the runtime of Kruskal’s algorithm? As we will see in future labs, sorting \(|E|\) edges will take \(O(|E| \lg |E|)\) time (just accept this fact for now!). The trickier part of Kruskal’s is determining if two vertices \(u\) and \(w\) are already connected. We could do a DFS or BFS starting from \(u\) and seeing if we visit \(w\), though we’d have to do this for each edge. What would be the resulting worst case runtime for Kruskal’s algorithm if it were implemented in this way?

Discuss with your partner.

Answer (click to reveal):

\(\Theta(EV)\).

Exercise 2: Using Disjoint Sets #

Instead, let’s revisit the data structure that specializes in determining if connections exist, the disjoint sets data structure. Each of the vertices of \(G\) will be an item in our data structure. Whenever we add an edge \((u, w)\) to \(T\), we can union the sets that \(u\) and \(w\) belong to. To check if there is already a path connecting \(u\) and \(w\), we can call find on both of them and see if they are part of the same set. Using this data structure, what is the runtime of Kruskal’s algorithm? (Note, this does account for the time used when creating the graph, just the time used in the algorithm itself.)

Discuss this with your partner.

Answer (click to reveal):

\(\Theta(E log(E))\)

To see a visual demonstration of Kruskal’s algorithm, see the Kruskal’s Demo.

In addition, the USFCA visualization can also be a helpful resource.

Exercise: Kruskal’s Algorithm #

Now, implement Kruskal’s algorithm using disjoint sets by filling out the method kruskals. You may also use techniques discussed in the Testing section above to test your implementation of Kruskal’s algorithm. For the disjoint set data structure, you may import the WeightedQuickUnionUF class but you may also use your implementation from Lab 15.

You may wonder how to sort the edges in Kruskal’s algorithm. If you look at the provided skeleton more closely, the Edge class implements Comparable, and our graph stores the edges in a TreeSet, in the instance variable called allEdges.

Handling Edge Cases in kruskals #

Similar to prims, if the graph is not connected, there is no way to create a spanning tree that includes all vertices. In this case, the kruskals method should return null. Try running Kruskal’s on the graph below, and see what happens!

Recall that the general logic of Kruskal’s is to add edges in increasing order of weight. Think about the following questions:

(1) After we iterated over all edges and checked all of them, how many edges should we have in a graph if we were to let the edges picked form a spanning tree?

(2) In the example graph above, how many edges do we actually have at the end?

(3) Based on this, how would you generalize the condition for when a graph is not connected when running Kruskal’s?

Deliverables #

As usual, remember to add, commit, push, submit, and add your partner on Gradescope.

To get credit for this lab:

• Complete the prims method.
• Complete the kruskals method.